Discrete Structures (CSCI 2824, Spring 2014)
Class Timings: MWF 10:00 - 10:50 AM
Class Location: Fleming 157
Instructor: Sriram Sankaranarayanan
Pre-Requisites: Data Structures (CSCI 2270) + ability to program in some language: preferably C++ or Python
Office Hours: We will have the following hours:
Agile office hours after class on MWF. Instructor will stay behind to provide quick help to students who stay behind as well.
Mondays: 3:15-4:30 PM, and Wednesdays: 12:15 - 1:15 PM.
Final Exam: Sat. May 3, 4:30 PM - 7:00 PM (Source: CU Boulder Academic Final Exam Schedule)
We will post and solve interesting puzzles throughout the semester: click here
Quiz # 5 will be held on April 30, 2014 (Wednesday) . It will cover all of combinatorics: counting, product rule, permutations, combinations, unordered counting, and binomial theorem.
Quiz # 4 will be held on April 14, 2014 (Monday) . It will cover functions, relations, one-to-one onto functions, and different types of relations.
Quiz # 3 will be held on March 14, 2014 (Friday) . It will cover proofs by contradiction, pigeon hole principle, sets and functions.
Quiz # 2 will be held on Friday Feb 21, 2014 (20 minutes, covering assignments 3,4).
Quiz # 1 will be held on Jan 31, 2014 (Friday) (15 minutes, in class quiz covering assignments 1, 2).
Jan 20, 2014 : No class or office hours on monday Jan 20th, due to MLK day campus holiday. Special office hours on Tuesday from 12:30 - 2:00 PM @ Engg. Center Office Tower ECOT 624.
Jan 15, 2014 : Assignment #1 posted. One part online on Coursera private site and other part posted here.
Jan 6, 2014 Course page is live!
Assignments
Important Note: These problems are in addition to questions for online assignment that are posted on our private coursera site.
Assignment 1 (Due date: Jan 22nd, 2014 @ 10 AM in class).
Solution: Solutions.
Assignment 2 (Due date: Jan 29nd, 2014 @ 10 AM in class).
Solution: Solutions.
Assignment 3 (Due date: Feb 10, 2014 @ 10 AM in class).
Solution: Solutions.
Assignment 4 (Due date: Feb 19, 2014 @ 10 AM in class).
Solution: Solutions.
Assignment 5 (Due date: March 3, 2014 @ 10 AM in class).
Solution: Solutions.
Assignment 6 (Due date: March 12, 2014 @ 10 AM in class).
Solution: Solutions.
Assignment 7 (Due date: April 9, 2014 @ 10 AM in class).
Solution: Solutions.
Assignment 8 (Due date: Monday, April 21, 2014 @ 10 AM in class).
Solution: Solutions.
Programming Assignment
Programming Assignment (Due date: Friday, April 4, 2014 @ midnight ).
Lecture Schedule and Notes
The schedule of lectures shown below is subject to change. We will post lecture notes for most topics and videos for selected topics. We will strive to post all material well in advance. Please take a look through them, and come prepared for class.
| ID | Date | Topics Covered | Book Sections | Lecture Notes (Click on Links) | Video |
| 1 | Jan 13th | Introductory Lecture: Binary Numbers | none | Lecture on Binary Numbers | |
| 2 | Jan 15th | Sequences | 1.1, 1.2 | Lecture on Sequences and Summations | See Private Coursera Page |
| 3 | Jan 17th | Summations, Products (from previous lecture). Start Propositional Logic: Propositions, Connectives and Truth Tables | 1.3 | Lecture on Propositional Logic | |
| Jan 20th | No class due to campus holiday for Martin Luther King day | ||||
| 4 | Jan 22nd | Logic: Compound connectives (from previous lecture). Start predicate logic: predicates, quantifiers. | 1.3, 1.4 | Lecture on Predicate Logic | |
| 5 | Jan 24th | Wrap up propositional and predicate logic. Start discussion on models of predicate logic. | 1.5 | Models of Predicate Logic | |
| 6 | Jan 27th | Models of Predicate Logic Formulas (continued). Implications, Converse, Contrapositives and a primer on proofs | 1.5, 2.1 | Implications | |
| 7 | Jan 29th | Implications and Primer on proofs (continued) | 2.1,2.2 | Proofs | |
| 8 | Jan 31st | Common mistakes during proofs. + Quiz #1 towards end of lecture. | 2.2 | ||
| 9 | Feb 3rd | Strategies for proving statements: universal statements, implications, existential statements. Proofs involving numbers. | 2.2 | Divisibility Proofs | |
| 10 | Feb 5th | Induction proofs: weak and strong induction. | 2.3 | Induction Proofs | |
| 11 | Feb 7th | Induction: practice sheet | 2.3 | Sheet | |
| 12 | Feb 10th | Strong Induction: Pitfalls | 2.4 | Strong Induction | |
| 13 | Feb 12th | Wrap up of induction: Induction on programs | 2.5 | ||
| 14 | Feb 14th | Proof by contradiction | 2.5,2.6 | Proofs by Contradiction | |
| 15 | Feb 17th | Pigeon hole principle | 2.6 | Pigeon Hole Principle | |
| 16 | Feb 19th | Introduction to Cryptography | Basics of Cryptography | ||
| 17 | Feb 21st | RSA Cryptosystem basics + Quiz # 2 | RSA | ||
| 18 | Feb 24th | RSA details | - reuse RSA notes - | ||
| 19 | Feb 26th | Sets: definitions, set operations | Sets | ||
| 20 | Feb 28th | Sets: cardinality, inclusion-exclusion principle, subsets | Proving Properties over Sets | ||
| 21 | Mar 3rd | Sets: power sets, proving properties Functions and Relations | Functions and Relations | ||
| 22 | Mar 5th | Compositions and inverses | Compositions and Inverses | ||
| 23 | Mar 7th | One-to-one and onto functions | One-to-one and Onto Functions | ||
| 24 | Mar 10th | Infinite sets, countability, degrees of infinity | Infinite Sets and Degrees of Infinity | ||
| 25 | Mar 12th | Cantor-Schroeder-Bernstein Theorem | -reuse lecture 24 notes - | ||
| 26 | Mar 14th | Types of relations: reflexive, symmetric, transitive, anti-symmetric, partial and total orders. Quiz # 3 | Relation Types | ||
| 26a | Mar 17th | Functional Programming Lecture # 1: Devin Coughlin | |||
| 26b | Mar 19th | Functional Programming Lecture # 2: William Mortl | |||
| 26c | Mar 21st | Functional Programming Wrapup #3: Nick Vanderweit | |||
| Mar 23 - 30 | Spring Break | ||||
| 27 | Mar 31st | Wrapup relations, equivalences | Equivalence Relations and Classes | ||
| 28 | Apr 2nd | Growth of functions: Big-OH, Big-Omega and Big-Theta | Growth Of Functions | ||
| 29 | Apr 4th | Wrap up + Introduction to Combinatorics | Introduction To Combinatorics | ||
| 30 | Apr 7th | Product, Sum and Complement rules. Permutations: Ordered choice with replacement. | Permutations | ||
| 31 | Apr 9th | Combinations: Unordered choice without replacement | Combinations | ||
| 32 | Apr 11th | Binomial Coefficients Binomial Theorem | Binomial Theorem & Unordered with Replacement | ||
| 33 | Apr 14th | Unordered Choice with replacement Quiz # 4 | reuse notes | ||
| 34 | Apr 16th | Counting by recurrences. | Recursive Counting: Setting up recurrences | ||
| 35 | Apr 18th | Solving recurrences (simple recurrences) | Solving recurrences | ||
| 36 | Apr 21rd | Graph Theory: Basic introduction, paths, cycles, walks, tours, Eulerian tours | Basic Graph Theory | ||
| 37 | Apr 23th | Connected components, bipartite graphs, and coloring. | Connectedness and Bipartite Graphs | ||
| 38 | Apr 25th | Trees, counting trees, Pruffer sequences and Catalan numbers | Trees | ||
| 39 | Apr 28th | -wrap up of syllabus- | |||
| 40 | Apr 30th | Quiz # 5 + | |||
| 41 | May 2nd | Revision |
Syllabus
The course covers fundamental ideas from discrete mathematics, especially for computer science students. It focuses on topics that will be foundational for future courses including algorithms, artificial intelligence, programming languages, automata theory, computer systems, cryptography, networks, computer/network security, databases, and compilers.
Why Discrete Structures?
Computer Science is all about solving interesting problems efficiently and cheaply, using computers! Here are some real problems that keep many computer scientists awake at night:
Route a packet reliably from one server to another on the internet (faster than existing protocols? even when routers can fail on us?)
Search for web pages (better than google, bing or your favorite search engine??)
Find the biggest clique on facebook. How many people are in this clique? Who are they?
Understand how to sequence the human genome.
Find all the prime factors for really large number (
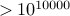 ).
).Write a program to play go (and play better than the best human champion?).
Write a program to check if a program is “correct” (keeps your instructor awake at night!).
Some of these problems are really hard to solve using a computer. No one knows if there are easy solutions to these problems and it would be nice to see efficient solutions in this century. In this course, we will cover the mathematical foundations that will help us formulate solutions to some of the real problems above. Specifically, we will learn
How to abstract using mathematical objects such as sets, relations, functions, trees and graphs.
How to count really well (until we fall asleep. :-) ).
How to reason like a pro (!!): obtain succinct water-tight proofs to guarantee that your solutions are correct, better than a competing solution and all that.
We will learn these cool mathematical facts, so that in the course of your education as a computer scientist, you will write cool programs to solve interesting problems involving automated reasoning, games, fractals, social networks and the human genome.
Topics Covered
Roughly, we will cover the following topics (some of them may be skipped depending on the time available).
Logic: Propositional and First Order Logic, Boolean Algebra.
Proofs: Primer on writing proofs, inductions, proof by contradiction.
Sets, Relations and Functions: Basic properties. Paradoxes in naive set theory. Infinite sets. Diagonalization.
Recursion: Recursive functions and recursively defined structures.
Combinatorics: Counting, binomial theorem, counting with recursion.
Trees: Definitions and properties of trees.
Graphs: Definitions and properties of graphs.
Example Applications: Artificial Intelligence (automated reasoning, game playing), Graphics (drawing fractals), Cryptography (rsa) and Networks (social network analysis).
Textbook
We will use the following textbook Discrete Mathematics: Mathematical Reasoning and Proof with Puzzles, Patterns and Games by Douglas E. Ensley and J. Winston Crawley
Beware: The “paperback” version of the book is the student solutions manual. Please make sure that you are not purchasing the student solutions manual. We will not need it for the course.
“New” and “Used” versions on-line (amazon, barnes-and-noble, half.com, …) are significantly less expensive.
Instructor will supplement book with lecture notes.
On the positive side, the book is very well written, and is a delight to read. Textbook purchase is optional mainly because it is an expensive textbook (purely personal opinion of your instructor). I would encourage you to consider buying the book, especially if the material in this course seems unfamiliar from your past experience.
Course Work
We will have weekly assignments that will be based on the assigned reading for each class. Additionally, we will have one or two programming assignments through the semester that will involve writing programs in any programming language of your choice.
Pre-Lecture Work
Before you attend each lecture, we hope that you will spend 10-15 minutes to prepare:
Read the required portion of the book (at least skim through the book or notes provided).
Watch any videos posted on-line (instructions will be sent via email).
Some lectures may contain a small 5-10 minute tutorial problem that we will solve as a class. After solving the problem, you are expected to submit it to the instructor. The resulting grade will count for your course participation.
Forums
We will set up forums that will allow students to interact with the course staff and with each other. You can participate in the forum and help answer questions posed by your classmates. Doing so counts towards your course participation score.
Weekly Assignments
We will assign weekly homework problem sets. Each problem will be due in a week from the date assigned. The problem sets will be posted on-line and will be of two types:
Simple multiple choice questions that will be autograded. You are allowed unlimited attempts at solving these problems. They are intended to help you learn by testing your concepts.
Written assignment: We will have one or two longer, more open ended questions. These have to be solved on paper and turned in at the beginning of the lecture on the due date.
No late submissions will be accepted for any reason other than documented medical emergencies.
To be flexible, we will omit two assignments with the lowest scores from consideration while computing the overall grade.
Programming Assignments
Programming assignments will involve writing programs to solve interesting problems using the ideas learned in class. These assignments will be used to crystallize some of the concepts that we will cover in this course.
A thorough working knowledge of some programming language: C, C++, Java, or Python is expected for this class.
Examinations
The course will have a quiz every 2-3 weeks. The dates for the quizzes will be posted well in advance. Each quiz will be 15-20 minutes long, and will focus on the material corresponding to a set of lectures.
No alternate exams will be offered unless there is a very compelling and documented personal or medical emergency. If you need special accommodations of any nature, you are expected to inform the instructor well in advance.
The lowest quiz will be dropped for the purposes of computing the grade.
It is compulsory to attend the final exam and score at least a 25% to obtain a pass in this course.
Course Participation
Class participation is awarded based mainly on your class preparation, as judged by your general attendance, classroom behavior, interaction in class, willingness to answer questions in class and at the on-line forums, and demonstrating knowledge of weekly reading during problem solving time.
Grading
The overall grade will be based on a cumulative score computed by adding together the grades from:
The weekly assignments (with least two scores omitted),
The programming assignments (ideally, we hope to have two assignments over the semester),
The grades from the quizzes (with least grade omitted).
The final exam.
Class participation: you are expected to attend class and in class you are expected to interact with the instructor.
Overall, the contributions to the final grades will be:
Assignments Weekly (25% of the grade).
Programming Assignments (10% of the grade).
In-Class Quizzes (35% of the grade cumulatively).
Final exam (20% of the grade).
Participation (10% of the grade).
The instructor may make minor modifications to this breakup as the semester progresses.
Note: To obtain a passing grade, the student has to appear for the final exam and obtain a score of at least 25/100 or above.
The final grades will be based on the cumulative score from all these factors (out of 100).
Collaboration Policy
The collaboration policy is rather simple:
Inspiration is free: you may discuss homework assignments with anyone. You are especially encouraged to discuss solutions with your instructor and your classmates.
Plagiarism is forbidden: the assignments that you turn in should be written entirely on your own. While writing the assignment you are not allowed to consult any source other than the textbook(s) for the class, your own class notes or the lecture notes for the class. Copying/consulting from the solution of another classmate constitutes a violation of the course's collaboration policy and the honor code.
Do not search for a solution on-line: You may not actively search for a solution to the problem from the internet. This includes posting to newsgroup or asking experts at other universities.
When in doubt, ask: If you have doubts about this policy or would like to discuss specific cases, please ask the instructor.
Honor Code
We will expect strict adherence to our our honor code. Please read and understand the code thoroughly. If in doubt, ask the instructor. At the end of the day, honor code violators hurt themselves by sacrificing their integrity and risking hard-earned reputation for a few measly grade points.