CSCI 2824: Lecture
These notes are for the part of lecture alphabet sequences for roughly the first 10-15 minutes of the lecture.
In this lecture, we will cover the following concepts:
Raymond Smullyan's liar and truth teller puzzles.
The truth table to analyze situations.
Propositional Logic, Connectives and Truth Tables.
Equivalence of Formulae, Tautologies and Fallacies.
This lecture corresponds to section 1.3 in Ensley and Crawley's book.
Logic
In a very crude sense, logic is the assembly language of mathematics (or philosophy). Logic can be defined as the study of reasoning itself or the study of techniques for drawing valid conclusions from premises. Understanding Logic is very important to computing at many levels. For instance, propositional Logic and propositional connectives such as AND, OR and NOT form the basic building block of digital circuits from which we build modern computers. Logic is also key to areas of CS such as automata theory, programming language semantics and artificial intelligence.
Smullyan's Liar/Truth-Teller Puzzles
Raymond Smullyan has written many books with puzzles that illustrate the beauty behind logic and formal systems (Instructor's favorite: To Mock A Mockingbird, a great way of thinking about combinatory Logic and functional programming).
The liar and truth teller puzzles all assume that we are on some island and there are two types of people on this island:
(Compulsive) Truth Tellers: They always tell the truth.
(Compulsive) Liars: They never tell the truth.
Each puzzle gives us some statements that people make and you have to analyze who is a liar and who is a truth teller. Assume that there are no physical characteristics to differentiate each type from the other.
Let us do some warm up questions:
Puzzle
Suppose I asked a person in this island the question: “Are you a liar?”. What would be their answer?
Puzzle
We meet two people in the island 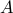 and
and 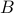 make the following remarks at the same time:
make the following remarks at the same time:
A says: “Exactly one of us is lying” and B says: “At least one of us is truthful”.
What can you conclude about the identities of A and B are they liars or are they truth tellers?
Puzzles like these are best analyzed using truth tables. The idea is that we are going to evaluate every possible situation and see which ones “make sense”.
Let us do this informally.
| A is truthteller? | B is truthteller? | A's statement is a lie | B's statement is a lie | Is this situation viable? |
| True | True | True | False | No, because, we assume that A is a ’'TruthTeller’’ when her statement is a lie |
| False | True | False | False | No, because A is assumed ’'liar’’ but is telling the truth. |
| True | False | False | False | No, because B is assumed ’'liar’’ but is telling the truth. |
| False | False | True | True | Yes! They are both assumed ’'liar’’ and their statements are both lies!! |
Puzzle
Let us try this in class:
A says “Exactly one of us is telling the truth”.
B says “We are all lying”.
C says “The other two are lying”.
Puzzle
This one is tricky but doable. Whoever first gives me the answer gets a free drink of their choice at the celestial seasonings cafe in the engineering lobby:
Two people A and B in the island are either both liars or both truth tellers. But we do not know which is the case. We wish to reach the castle which is either on path to the left or the path to the right. What question should we ask one or both of them so that we can find out which path leads to the castle?
Note The question or questions that you ask have to be explicitly about the castle and whether to take left or right. The instructors gut reaction was to ask A if Socrates is still alive (or the sun rose in the east yesterday) and B which is the way to the castle, but that does not count apparently!!
Propositional Logic
What are propositions? Propositions are simply statements that can receive a true or false valuation.
Examples of propositions:
“Socrates is mortal”.
“Jenny went to lunch with Craig”.
“I am telling the truth”.
“The quick brown fox jumped over the lazy brown dog”.
While studying propositional logic, we do not really care about what the proposition itself “means” just that it is either true or it is false.
Therefore, we simply use propositional variables (also called Boolean variables) to represent propositions. Why this? Just makes it nice and algebra like.
We use letters like 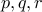 and so on to represent propositions.
and so on to represent propositions.
Propositional Logic Formulae
Formulae in propositional logic are defined as follows:
Any propositional variable is a formula.
If
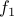 and
and 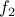 are formulas, then
are formulas, then 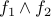 (read as
(read as 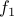 AND
AND 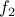 ) is a formula.
) is a formula. If
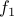 and
and 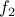 are formulas, then
are formulas, then 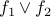 (read as
(read as 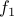 OR
OR 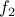 ) is a formula.
) is a formula. If
 is a formula then
is a formula then 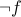 (read as NOT
(read as NOT  ) is a formula.
) is a formula.
Let us try some examples. Read the following propositional formulae aloud:
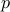
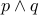
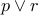
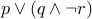
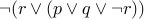 .
.
We evaluate propositional formulae using truth tables.
Truth Table for AND
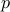 | 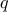 | 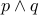 |
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
Each row represents some kind of a situation. For example, the top most row represents the
situation when propositions 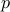 and
and 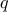 are both ’'true’’. Then we conclude that the
formula
are both ’'true’’. Then we conclude that the
formula 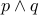 in this situation is also ’'true’’.
in this situation is also ’'true’’.
Logicians call these situations models. In this case, a Logician would
say that the truth assignment 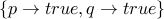 is a model
of the formula
is a model
of the formula 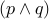 . In other words, if you imagine
a situation wherein the proposition
. In other words, if you imagine
a situation wherein the proposition 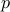 is true and the proposition
is true and the proposition 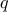 is true then
in that situation formula
is true then
in that situation formula 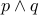 is true.
is true.
To avoid confusion let us use the term “situations” and “models”. We will formalize models later for first-order (predicate) logic.
Truth Table for OR
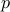 | 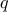 | 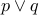 |
| T | T | T |
| T | F | T |
| F | T | T |
| F | F | F |
Can you write down all the models of 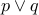 (read
(read 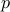 OR
OR 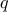 )?
)?
Does this correspond to your conception of 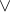 (the logical connective OR)?
(the logical connective OR)?
Truth Table for NOT
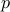 | 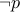 |
| T | F |
| F | T |
Truth Table for Compound Formulae
XOR is an important derived connective that is defined in terms of
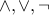 . It has the interpretation of “either-or”: i.e, either p or q, but not both.
. It has the interpretation of “either-or”: i.e, either p or q, but not both.
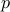 XOR
XOR 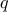 is the formula
is the formula 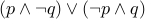 .
.
Its truth table can be written as below:
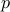 | 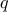 | 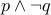 | 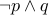 | 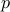 XOR XOR 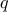 |
| T | F | T | F | T |
| T | T | F | F | F |
| F | T | F | T | T |
| F | F | F | F | F |
We will go through few more examples of truth tables in the book.
Other examples of derived connectives are:
Implication
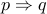 is defined as
is defined as 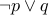 (we will study this in detail next week).
(we will study this in detail next week). Equivalence
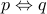 is defined as
is defined as 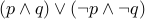 .
. Nand (a.k.a not of and)
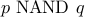 is defined as
is defined as 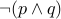 .
. NOR (a.k.a not of or )
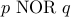 is defined as
is defined as 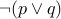
Let us write the truth table for the 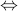 connective (equivalence connective):
connective (equivalence connective):
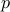 | 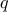 | 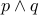 | 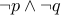 | 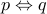 |
| T | F | F | F | F |
| T | T | T | F | T |
| F | T | F | F | F |
| F | F | F | T | T |
Tautology, Fallacies and Equivalence
Tautology
A formula is a tautology if and only if it is true no matter what value one gives to the propositions involved in the formula.
Example is 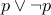 .
.
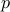 | 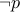 | 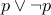 |
| T | F | T |
| F | T | T |
No matter what you value one gives 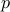 , the formula
, the formula 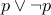 is always true.
is always true.
Other examples of tautology are
 (De Morgan's Law).
(De Morgan's Law). 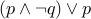 (also written as
(also written as 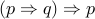 ).
). 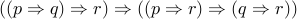 (do not even try expanding this :-)
(do not even try expanding this :-)
Fallacies
Fallacies are the opposite of tautologies. These are formulae that are false no matter what the truth values of the propositions in them.
Example: 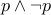 .
.
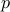 | 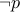 | 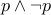 |
| T | F | F |
| F | T | F |
If we take a tautology and negate it then it becomes a fallacy.
Therefore 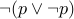 is a fallacy.
is a fallacy.
Logical Equivalence
Two formulae are logically equivalent if and only if they have the same truth value in each row of the (joint) truth table.
Example:
The formulae 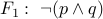 and
and 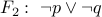 are logically equivalent.
To see why let us write their truth tables (we tack them together for convenience).
are logically equivalent.
To see why let us write their truth tables (we tack them together for convenience).
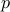 | 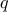 | 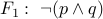 | 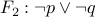 |
| T | T | F | F |
| F | T | T | T |
| T | F | T | T |
| F | F | T | T |
Notice that for all the truth table rows, 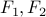 coincide.
coincide.
Examples of equivalent formulae include
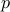 and
and 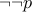 .
. 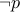 and
and 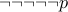 .
. 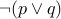 and
and 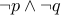 (De-Morgan's law).
(De-Morgan's law).
Technically, you need not assume that the formulae have the same set of propositions. For example, 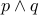 and
and
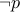 are not logically equivalent. However,
are not logically equivalent. However, 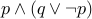 and
and 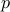 are logically equivalent.
are logically equivalent.
Similarly, 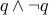 and
and 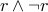 are logically equivalent since they are both fallacies.
are logically equivalent since they are both fallacies.
Theorem:
Statement of Theorem:
Whenever two formulae 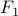 and
and 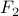 are equivalent then
are equivalent then  is a tautology.
is a tautology.
Proof: Consider the truth table for the formula  generated from a truth table
that has a column for
generated from a truth table
that has a column for 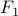 and a column for
and a column for 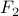 (as shown below).
(as shown below).
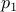 | 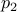 |  | 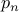 | 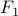 | 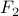 |  |
| T | T |  | F | F | F | T |
 |  |  |  |  |  |  |
| F | F |  | T | T | T | T |
Note that for  column to have a false entry at some row,
column to have a false entry at some row, 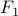 and
and 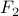 must have different
values at that row. But since
must have different
values at that row. But since 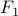 is logically equivalent to
is logically equivalent to 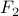 , they always have the same value at each row.
, they always have the same value at each row.
As a result, the  column must be all true, for all the rows in the truth table. Therefore
it is a tautology.
column must be all true, for all the rows in the truth table. Therefore
it is a tautology.