CSCI 2824 Lecture 25 Notes: Binomial Theorem
In this lecture, we will continue with the binomial theorem and look at some applications. We will also look at recursive counting and counting unordered lists with repetitions.
Biniomial Theorem
For all natural numbers  , we can expand
, we can expand
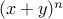 as
as
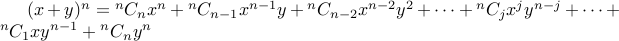
We can write it succinctly as 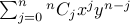 .
.
Proof What is the coefficient of 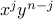 in
in 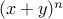 .
We write
.
We write 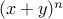 as
as 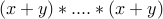 .
There are
.
There are  multiplicands.
multiplicands.
To form a term 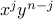 where
where 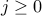 , we can choose
, we can choose 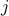 out of
out of  multiplicands to “supply” the
multiplicands to “supply” the 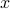 . The remaining will be chosen automatically to supply the
. The remaining will be chosen automatically to supply the 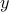 s.
There are
s.
There are 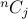 choices. Each choice appears as a term which are then collected up.
choices. Each choice appears as a term which are then collected up.
Our reasoning above shows that the coefficient of 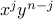 where
where 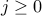 should be
should be 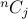 .
.
Applications of Binomial Theorem
We can use the Binomial theorem to show some properties of the 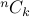 function.
function.
1. 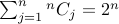 .
.
Proof: Take the expansion of 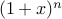 and substitute
and substitute 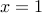 .
.
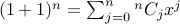
2. Let  be an even number. Then we have
be an even number. Then we have 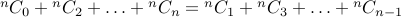 .
.
Proof: Take 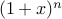 and set
and set 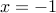 . Write a similar result for
. Write a similar result for  odd.
odd.
3. Evaluate: 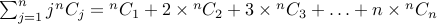 .
.
Proof: Take 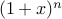 . Using binomial theorem, we have
. Using binomial theorem, we have
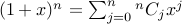 .
.
Take the derivative of both sides w.r.t 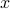 . We get:
. We get:
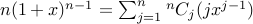
Substituting 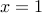 , we get the required summation to be
, we get the required summation to be 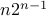 .
.
4. Likewise, can you evaluate this summation:
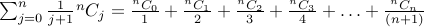
Counting Unordered Lists With Repetition
Here is a problem: There are ten candy stores, each selling the same type of candy. How many ways are there for me to purchase 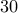 candies from these
candies from these 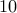 stores?
stores?
I could purchase all
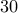 from one store.
from one store.I could purchase
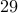 from one store and one more from another store.
from one store and one more from another store.I could purchase
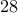 from one store, and one each from two other stores.
from one store, and one each from two other stores.I could purchase
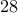 from one of the stores and two from another store…
from one of the stores and two from another store…Ah.. the possibilities :-)
In other words, we are asking, how many ways are there of satisfying the following equation:
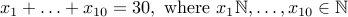
Note that 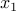 refers to the number of candy bought from the first store any number ranging from
refers to the number of candy bought from the first store any number ranging from 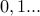 .
Similarly,
.
Similarly, 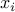 refers to number of candy bought from
refers to number of candy bought from 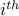 store. Again, we can buy any natural number.
Note that we cannot buy negative number of candies.
store. Again, we can buy any natural number.
Note that we cannot buy negative number of candies.
Naturally each of the 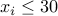 but we
do not add that explicitly. The only way
but we
do not add that explicitly. The only way 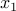 can be
can be 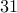 is some other
is some other 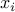 is negative, which cannot
happen.
is negative, which cannot
happen.
Candy Purchasing and Binary Sequence
We will now “code up” the patterns of candy purchasing using binary strings made up of 0s and 1s.
Take a sequence of 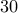 0's. Each 0 represents a candy.
0's. Each 0 represents a candy.
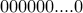
Our goal is to insert 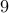 ’1's somewhere in this sequence. Eg.,
’1's somewhere in this sequence. Eg.,
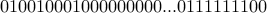
We interpret the sequence above to mean,
Bought 1 candy from first store.
Bought 2 candy from second store.
Bought 3 candy from third store.
Bought 23 candy from store
Bought 2 candy from store
Let us take another example: Take another sequence of 0's and 1's with 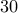 0s and 9 1s.
0s and 9 1s.
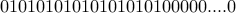
What pattern of candy buying does it represent:
1 candy from store 1
1 candy from store 2
1 candy from store 9
21 candies from store 10.
What pattern of 0s and 1s represent the following pattern of candy purchasing?
0 candies from stores 1-5.
1 candy from store 6.
28 candies from store 7
0 candies from store 8
1 from store 9
0 from store 10.
Answer:
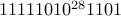
Claim
1. There is a one-to-one correspondence between the patterns of purchasing 30 candies from 10 stores and the number of binary sequences consisting of 30 0's and 9 1's.
2. There is a one-to-one corr. between the patterns of purchasing 30 candies from 10 stores and the number of solutions to the equation:
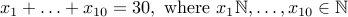
Answer
There are ten candy stores, each selling the same type of candy. How many ways are there for me to purchase 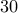 candies from these
candies from these 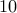 stores?
stores?
Answer We have a corr. between each pattern of candy purchasing and a binary sequence with exactly 30 0's and 9 1's.
Therefore, the required answer is simply 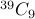 (or
(or 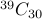 ).
).
Unordered Lists With Repetitions
1. Let us say we have  different bags each containing unlimited quantities of an item. How many ways are there of choosing
different bags each containing unlimited quantities of an item. How many ways are there of choosing  items from these bags?
items from these bags?
Or equivalently,
2. What are the number of solutions to the equation:
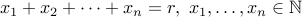
or equivalently,
3. How many binary sequences of 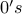 and
and 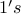 exist with precisely
exist with precisely  0's and
0's and 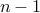 1's?
1's?
Answer to all of these problems is 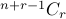 .
.
Example-1
How many natural number solutions are there for the equation: 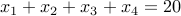 ?
?
Answer Each solution can be viewed as inserting 3 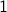 s in between
s in between 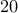 zeros. This gives us
zeros. This gives us 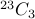 .
.
Example-2
How many natural number solutions are there for the equation: 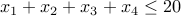 ?
?
Answer We can write the problem equivalently as  , where
, where 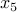 is a slack variable representing the left-over quantity
is a slack variable representing the left-over quantity
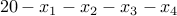 which must be a natural number
which must be a natural number 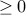 . Therefore, the answer is inserting
. Therefore, the answer is inserting 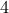 1s between
1s between 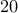 zeros:
zeros: 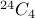 .
.
Example-3
How many positive integer solutions are there for the equation: 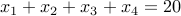 ?
?
We require 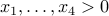 . Let us simply write
. Let us simply write 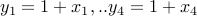 . We have
. We have 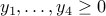 and
and
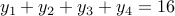 .
.
This gives us 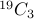 solutions.
solutions.
Example-4
There are three shops that sell widgets. Our goal is to obtain 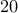 widgets in all. But we are constrained to buy at least
widgets in all. But we are constrained to buy at least 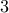 from each shop.
How many ways of widget buying are available?
from each shop.
How many ways of widget buying are available?
Recursive Counting
In recursive counting, we express the count as a recurrence relation.
Example-1
How many round-robin matches need to be played between 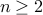 teams?
teams?
We know that the answer is 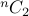 .
.
Answer Let 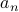 be the number of round-robin matches that
be the number of round-robin matches that  teams need to play.
If
teams need to play.
If 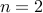 , we know that
, we know that 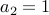 .
.
Let us write a recurrence for 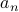 . We note that team
teams
. We note that team
teams 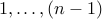 ).
Therefore
).
Therefore
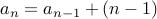
where 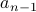 counts the number of round robin matches played all teams other than the last team
and
counts the number of round robin matches played all teams other than the last team
and 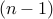 accounts for the last team.
accounts for the last team.