CSCI 2824 Lecture # 6 Notes
In the previous lectures, we studied implications. This lecture will focus on implications and start chapter 2 on proof techniques.
Implications: Converse and Contrapositive. Negation of an implication.
Primer on writing proofs (Section 2.1).
Implications: Contrapositive and Converse
In simple terms, if 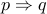 is an implication then
is an implication then
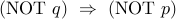 is its contra-positive.
is its contra-positive. 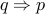 is its converse.
is its converse.
This is a very common source of confusion.
Examples:
For all integers
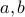 , if
, if 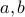 are both odd then
are both odd then 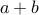 is even.
is even. Contrapositive: For all integers
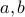 , If
, If 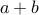 is not even then both
is not even then both 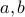 cannot be odd. (Is this true?)
cannot be odd. (Is this true?) Converse: For all integers
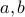 , If
, If 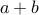 is even then
is even then 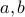 are both odd. (Is this true?)
are both odd. (Is this true?)
If
 is odd then
is odd then 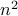 is odd.
is odd. Contrapositive: If
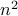 is not odd then
is not odd then  is not odd. (Is this true?)
is not odd. (Is this true?) Converse: If
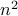 is odd then
is odd then  is odd. (Is this true?)
is odd. (Is this true?)
Claim: Any implication is logically equivalent to its contra-positive.
Proof: We are asked to prove in effect that 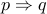 is logically equivalent
to
is logically equivalent
to 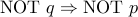 . We write down the truth table to verify this fact.
. We write down the truth table to verify this fact.
QED.
The Converse Trap
Proving the converse of a statement is often a trap that even experienced researchers can fall into. Note that proving the converse of an implication in no way convinces us of the truth of the implication.
Let us take examples from real life to see how silly it could be:
Statement If a person is underage and consumes of alcoholic beverages then he/she is breaking the law.
Converse If a person is breaking the law then he/she consumes alcoholic beverages.
Does the converse ring true?
Primer on Proofs and Mathematical Writing
This lecture, we will warm up by practicing some proofs and the right way to express those proofs. A proof is meant to convince people that some mathematical fact is true. It is meant to be read and judged by ones peers. Therefore writing proofs out well is an important skill for discrete mathematics.
Example # 0
Let us prove the following statement.
Claim: If  is even then
is even then 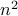 is even. In Logical notation:
is even. In Logical notation: 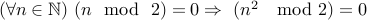 .
.
Dear reader,
You have expressed criticism to my theorem in the annals of CSCI 2824 that can be written as
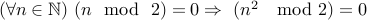
If you were kind enough to provide me with any number that we will call  , then there are two cases:
, then there are two cases:
You provided me with an odd number
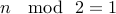 . The antecedent of the implication is false. Therefore, the implication itself holds true. I have nothing else to say to you in this case.
. The antecedent of the implication is false. Therefore, the implication itself holds true. I have nothing else to say to you in this case. If, however, you were clever enough to provide me with an even value of
 , we may of course write it in the form
, we may of course write it in the form 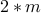 for some number
for some number 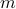 . Also,
. Also, 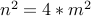 by elementary algebra. As you know
by elementary algebra. As you know 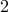 divides
divides 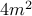 which is the same as
which is the same as 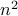 . Therefore
. Therefore 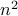 is even.
is even.
Thus, in no case, can you produce a number  that satisfies the antecedent
that satisfies the antecedent 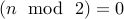 but violates the consequent (
but violates the consequent (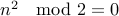 ).
I remain your faithful prover of claims.
).
I remain your faithful prover of claims.
A fond adieu to you, and you and you,
Note to class: Never, ever, write a dear reader letter
Write the proof in more sensible language.
Proof: Let  be any given number. If
be any given number. If  is odd, then the statement holds true vacuously. Otherwise,
is odd, then the statement holds true vacuously. Otherwise, 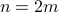 for some number
for some number 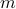 .
Therefore,
.
Therefore, 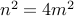 . We see that
. We see that 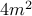 is divisible by
is divisible by 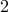 . Therefore
. Therefore 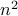 is even.
is even.
QED.
Example# 1
Claim: For 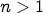 , If
, If  is even
is even 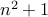 is prime. I.e,
is prime. I.e, 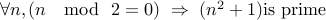 .
.
Proof Attempt 1: Let us test for 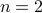 , we have
, we have 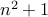 is 5. Works. It also works for
is 5. Works. It also works for 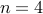 since
since 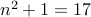 is prime and
is prime and
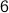 since
since 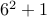 is prime. Therefore,
is prime. Therefore, 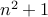 is prime if
is prime if  is prime.
is prime.
Let us attempt one more proof of this:
Proof-2: Assume 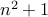 is prime. We will prove that
is prime. We will prove that  must be even.
must be even.
Since
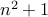 is prime, and
is prime, and 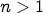 ,
, 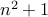 must necessarily be odd.
must necessarily be odd. Since
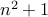 is odd, it must be the case that
is odd, it must be the case that 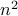 is even.
is even.If
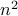 is even, we have proved previously that
is even, we have proved previously that  is also even.
is also even.Therefore,
 is even.
QED??
is even.
QED??
Are there any flaws in either of these proofs? Do they convince you of the truth of our “claim”?
Example #2
Claim If two numbers  and
and 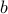 are odd, then
are odd, then 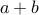 is even.
is even.
Write this down in logical notation?

Let us look at a proof:
Proof Here are our reasoning steps:
Since
 is odd, it can be written as
is odd, it can be written as 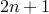 for some
for some  .
. Since
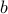 is odd, it can be written as
is odd, it can be written as 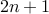 too.
too. Therefore
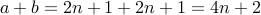 .
. But
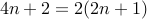 is an even number.
is an even number. Therefore,
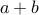 is even.
QED.
is even.
QED.
Is there anything wrong with the proof above?
Now let us look at a related claim:
Claim If two numbers  and
and 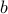 are odd, then
are odd, then 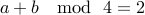 .
.
Exercise: Write this statement down in Predicate Logic. Is this a true statement?
Proof Here are our reasoning steps:
Since
 is odd, it can be written as
is odd, it can be written as 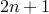 for some
for some  .
. Since
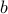 is odd, it can be written as
is odd, it can be written as 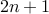 too.
too. Therefore
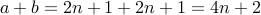 .
. 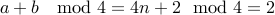 .
. Therefore,
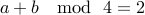 .
QED.
.
QED.
Can you correct the demonstrations above? What went wrong?
More Complicated Proof
Claim If  is natural number then
is natural number then 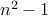 is a composite number.
is a composite number.
Before we dive further, what is a composite number?
A natural number  is composite if it can be written as
is composite if it can be written as 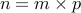 with
with 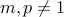 .
.
The provision that 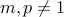 is very important. Or else any number
is very important. Or else any number
 can trivially be written as
can trivially be written as
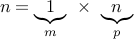 ,
,
with 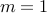 and
and 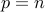 .
.
Now, back to our claim.
Claim If  is natural number then
is natural number then 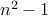 is a composite number.
is a composite number.
Proof: Let  be a natural number.
be a natural number.
We can write
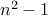 as a product of
as a product of 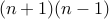 .
. Therefore
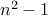 is a composite number.
QED??
is a composite number.
QED??
Have we really proved the claim above?