CSCI 2824 Lecture 29: Graph Theory (Basics)
In this lecture, we will study graphs and some very basic properties of graphs. We will conclude by studying the concept of Eulerian tours.
Directed Graphs
We have already encountered graphs before when we studied relations. We viewed graphs as ways of picturing relations over sets.
A directed graph 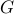 consists of a finite set of nodes (or vertices)
consists of a finite set of nodes (or vertices) 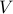 and a set of edges
and a set of edges 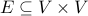 .
.
Each edge is a tuple
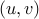 where
where 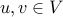 are vertices of the graph.
are vertices of the graph. The set of edges
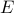 is a relation over
is a relation over 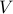 .
.
We draw a graph 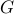 by drawing circles to represent each of its
vertices and arrows to represent edges. The edge
by drawing circles to represent each of its
vertices and arrows to represent edges. The edge 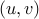 is
represented by an arrow from
is
represented by an arrow from 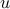 to
to  . The direction of the arrow
points from
. The direction of the arrow
points from 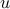 to
to  . The arrows have a direction and therefore the
graph is a directed graph.
. The arrows have a direction and therefore the
graph is a directed graph.
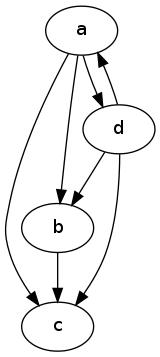
Example-1
Take  and
and 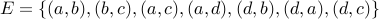 . Here is how we draw this graph:
. Here is how we draw this graph:
Example-2
Take 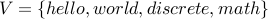 and
and  .
.
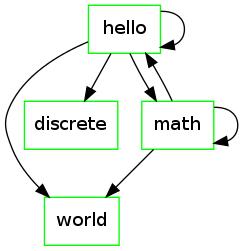
The edge  and the edge
and the edge  are called self-loops, since they point from a vertex to itself.
are called self-loops, since they point from a vertex to itself.
In the study of graphs, will assume that any graph we look at does not have self loops. Most of the results discussed below applies to graphs without self-loops.
Why Study Graphs?
Graphs are useful in a variety of situations. Graph models are really common representations of networks (computer networks, social networks, protein networks,…). It is very useful to model a variety of entities as graphs and study their structure:
Eg., set of nodes = people on facebook and edges = friendship. Prof. Clauset's group at CU Boulder specializes on such graphs, among many others.
Eg., set of nodes = proteins and edges = protein-protein interactions. Our bioinformatics research group (Prof. Goldberg) looks at such interactions in graphs.
Eg., set of nodes = web pages and edges = links between pages.
Undirected Graphs
So far, we have studied directed graphs, which are just representations of relations over finite sets (assume that there are no self-loops). An undirected graph is a special kind of directed graph that occurs when the edge relation is symmetric.
An undirected graph 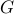 is a set of vertices
is a set of vertices 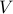 along with a set of edges
along with a set of edges 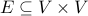 such that the relation
such that the relation 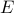 is symmetric:
is symmetric:
Whenever the edge
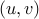 exists in an undirected graph then so does the edge
exists in an undirected graph then so does the edge 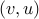 .
.
As a result, we draw an undirected graph by not drawing placing any arrows on the edges. Edges are simply straight-lines. Alternatively, we could have represented each edge by a double arrow, one in each direction or two sets of arrows. These are all equivalent.
Example-1
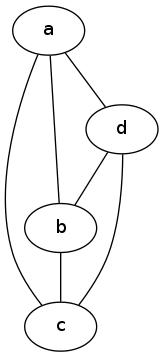
Consider the undirected graph  :
:  and
and 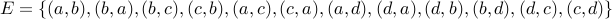 . Verify that the relation represented by
. Verify that the relation represented by 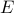 is
indeed symmetric. Here is how we draw this graph:
is
indeed symmetric. Here is how we draw this graph:
Example-2
Take 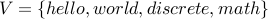 and
and  .
.
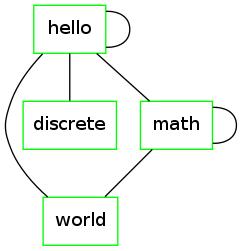
Once again, this graph has self loops. But we will silently assume, henceforth, that there are no self-loops.
Representing Graphs
There are two ways of representing a graph inside a computer: adjacency list or a adjacency matrix. You should already be aware of adjacency list and matrix representations of graphs from your data-structures class (please email me if you are not). We will not go into these concepts here.
Degrees and Degree Sequences
In/Out Degree
Let 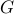 be a directed graph with vertex set
be a directed graph with vertex set 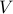 and edge set
and edge set 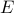 .
.
The set of incoming edges of a vertex  are all those edges whose arrows point into
are all those edges whose arrows point into  :
:
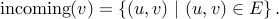
In-Degree For any vertex 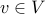 , the in-degree of
, the in-degree of  is the
number of incoming edges into
is the
number of incoming edges into  .
.
Similarly, we can define outgoing edges for a given vertex  :
:
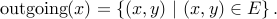
For any vertex 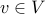 , the out-degree of
, the out-degree of  is the number of outgoing edges out of
is the number of outgoing edges out of  .
.
Note For a undirected graph, the set of incoming edges is the same as the set of out-going edges for any vertex
The degree of a vertex  in an undirected graph is the number of
(we can say either incoming or outgoing) edges that are incident on
in an undirected graph is the number of
(we can say either incoming or outgoing) edges that are incident on
 .
.
Note that the concepts of in-degree and out-degree coincide with that of degree for an undirected graph.
Degree Sequences
Let us take an undirected graph 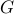 without any self-loops. Going
through the vertices of the graph, we simply list the degree of each
vertex to obtain a sequence of numbers. Let us call it the degree
sequence of a graph. The degree sequence is simply a list of numbers,
often sorted.
without any self-loops. Going
through the vertices of the graph, we simply list the degree of each
vertex to obtain a sequence of numbers. Let us call it the degree
sequence of a graph. The degree sequence is simply a list of numbers,
often sorted.
Example-1
Consider the undirected graph 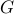 :
:  and
and  .
.

| Node | Degree |
| a | 3 |
| b | 3 |
| c | 3 |
| d | 3 |
The degree sequence is  .
.
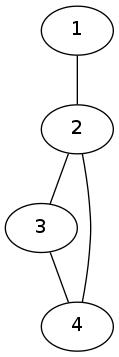
Example-2
Here is a graph with degree sequence 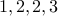 .
.
Example-3
Can you construct a graph with a degree sequence  ?
?
It needs to have three vertices 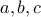 and a single edge between
and a single edge between 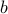 and
and  and no edges to
and no edges to  .
.

Properties of Degree Sequences
Given a undirected graph 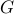 without self-loops, what can we say about its degree sequence?
without self-loops, what can we say about its degree sequence?
Example-1
Can there be an undirected graph (no self-loops allowed) with degree sequence 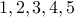 ?
?
There can be no such graph.
Let us try to construct such a graph. How many nodes does it need to
have? from the degree sequence, we know that it has 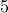 nodes. Now
note that there must be a node with degree
nodes. Now
note that there must be a node with degree 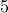 according to the given
degree sequence. However, every node can have between
according to the given
degree sequence. However, every node can have between  and
and 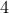 edges.
edges.
Sum of Degree Sequence
For an undirected graph 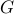 without self-loops, the sum of all the numbers in its degree sequence is exactly twice the number of edges.
without self-loops, the sum of all the numbers in its degree sequence is exactly twice the number of edges.
In other words, let 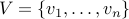 be the vertex set of an
undirected graphs with no self-loops and
be the vertex set of an
undirected graphs with no self-loops and 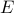 be the edge set. Let us
write the degree of a node
be the edge set. Let us
write the degree of a node 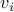 as
as 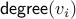 . We
conclude that
. We
conclude that
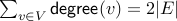
By summing up the degree of each vertex, we are counting all edges
that are incident on that vertex. In this summation, therefore each
edge 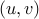 in the graph contributes to a value of
in the graph contributes to a value of 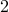 (one for the
degree of
(one for the
degree of 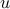 and one for the degree of
and one for the degree of  ). Therefore, we conclude
that the summation is twice the number of edges.
). Therefore, we conclude
that the summation is twice the number of edges.
As a consequence, the summation of a degree sequence must be even.
Example
Is it possible to have a graph (no self-loops allowed, remember) with
the following degree sequence 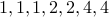 ?
?
Answer is no since the sum of the degree sequence is  which is an odd number.
which is an odd number.
Degree Sequence and Pigeon Hole Principle
Let 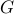 be an undirected graph so that
be an undirected graph so that
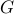 has no self-loops
has no self-loopsevery vertex of
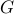 has some edge that incident on it (there are no degree
has some edge that incident on it (there are no degree  vertices).
At least two vertices in the graph must have the same degree.
vertices).
At least two vertices in the graph must have the same degree.
The proof is simple application of the pigeon-hole principle. In 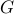 , every vertex can have a degree between
, every vertex can have a degree between 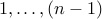 , where
, where
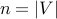 is the total number of vertices. This means that there are
is the total number of vertices. This means that there are 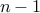 possible degrees (holes) and
possible degrees (holes) and 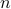 possible vertices (pigeons).
Therefore two vertices must have the same degree.
possible vertices (pigeons).
Therefore two vertices must have the same degree.
In/Out degress for directed Graphs
For a directed graph 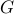 with vertices
with vertices 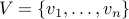 and edges
and edges 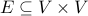 , we observe that
, we observe that

In other words, the sum of in-degrees of each vertex coincided with the sum of out-degrees, both of which equal the number of edges in the graph.
This is because, every edge is incoming to exactly one node and
outgoing to exactly one node. Therefore summing up all the in-degrees,
counts very edge 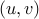 precisely once, when we add up
precisely once, when we add up
 . Similar reasoning applies to out-degrees too.
. Similar reasoning applies to out-degrees too.
Walk
Given a graph 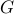 (can be directed or undirected), with vertices
(can be directed or undirected), with vertices 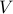 and edges
and edges 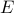 , a walk of the graph is a sequence of alternating vertices
and edges such that
, a walk of the graph is a sequence of alternating vertices
and edges such that
We can start our walk at any vertex and end at any vertex.
A single step of the walk takes an outgoing edge from current vertex to visit a neighbouring vertex.
A walk has to respect the edge direction. In other words, if we go
from vertex 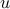 to vertex
to vertex  in a single step then the edge
in a single step then the edge 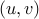 must be present. This is important for directed graphs and is trivial
for undirected graphs.
must be present. This is important for directed graphs and is trivial
for undirected graphs.
Example-1
Take the graph:

Here is a walk:
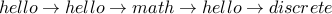
Here is another example of a walk:
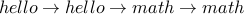
Here is an example of a sequence that is not a walk:
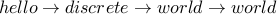
There is no edge from 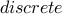 to
to 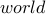 . So our walk cannot go in one step from
. So our walk cannot go in one step from 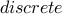 to
to 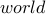 .
.
Example-2
Take the graph:

Here are some walks
 (just start and stop at
(just start and stop at  ).
). 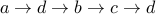 .
. 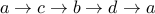 .
.
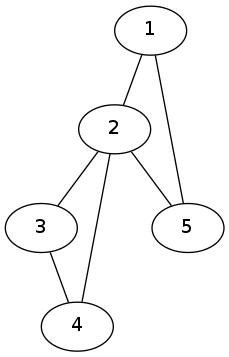
Paths
A path in a graph is a walk that does not repeat any vertices. The length of a path is the number of edges traversed by the path and one less than the number of vertices traversed.
Consider, again, the graph below:

Examples of paths include:
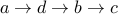 (it is a path of length 3)
(it is a path of length 3)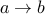 (it is a path of length 1)
(it is a path of length 1) (trivially it is a path of length 0)
(trivially it is a path of length 0)
Non-examples of paths include:
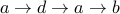 . This is a walk but not a path since it repeats the vertex
. This is a walk but not a path since it repeats the vertex  .
.
Eulerian Tour
Read about the Koenigsberg bridge problem here: Seven Bridges of Koenigsberg.
Here is the map of Koenigsberg in Germany where the famous mathematician Leonard Euler lived:

The green ovals show the bridges. Question is can we take a tour of each of the bridges:
starting anywhere we like as long as we return to our starting point
traversing each of the bridges exactly once.
We can ask the same question on the following graph which represents the topology


Is the connection between the original “topology” of the bridges and graphs clear?
If so, then the problem can be stated as:
Let us “walk” the graph starting from any vertex and traversing any edge that takes us to a neighbouring vertex and so on, such that
Each edge can be traversed at least once in either direction.
We have to end the walk at the same vertex where we began.
Eulerian Tour
An Eulerian tour is a special walk of the graph with the following conditions:
The walk starts and stops at the same vertex
Every edge in the graph is traversed exactly once during the tour.
Example-1
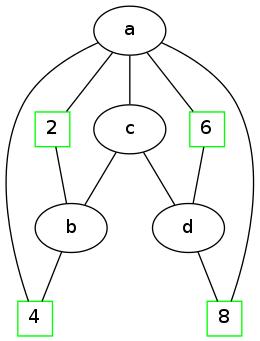
Does this graph have an Eulerian Tour:
Yes, here is a tour: 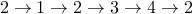 .
.
We started from 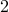 and ended at
and ended at 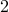 . Also note that we have traversed each of the six edges in the graph
exactly once.
. Also note that we have traversed each of the six edges in the graph
exactly once.
Example-2
What about this graph?

It does not have a tour.
This is the graph, we derived from the Konigsberg bridge problem. Turns out that we cannot have an Eulerian tour here.
To see this, let us focus on the vertex labelled  .
.
 has three edges incident on it.
has three edges incident on it. The walk must traverse each of the
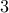 edges. Let us assume that the walk does not start at
edges. Let us assume that the walk does not start at  . If it does, we can simply do the following reasoning about the node
. If it does, we can simply do the following reasoning about the node 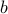 , instead.
, instead. We must enter
 by one of the edges for the first time and leave it by another edge. This leaves one edge untraversed.
by one of the edges for the first time and leave it by another edge. This leaves one edge untraversed. But we can only use the untraversed edge to enter
 and thence we will be stuck (since all the other edges are traversed).
and thence we will be stuck (since all the other edges are traversed).
An undirected, connected graph 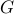 (without self-loops) has an
Eulerian tour if and only if every vertex in the graph has an even
degree.
(without self-loops) has an
Eulerian tour if and only if every vertex in the graph has an even
degree.
Since the graph of Konigsberg bridge problem has vertices  with
odd degree, it cannot have an Eulerian tour. Interestingly, there is
an efficient algorithm called Fleury's Algorithm that can be used to
construct an Eulerian tour if the given graph has all vertices with
even degree.
with
odd degree, it cannot have an Eulerian tour. Interestingly, there is
an efficient algorithm called Fleury's Algorithm that can be used to
construct an Eulerian tour if the given graph has all vertices with
even degree.