CSCI 2824: Lecture 9
In this lecture we will talk about the principle of mathematical induction and attempt to prove properties of numbers using induction.
This lecture corresponds to section 2.3 of Ensley and Crawley's book.
Mathematical Induction
Mathematical induction is a very common technique for proving properties of natural numbers (and other discrete structures such as sets, relations and trees that we will study very soon).
Here is a video of falling dominoes: Click here.
Let us imagine an infinitely long sequence of tiles arranged in a straight line (close enough to each other), and let us tip domino number 1.
We wish to argue that every domino will fall. Here is how we can argue:
Base case: The first domino falls (we kicked it, so it falls).
Inductive Step: Whenever a domino numbered n falls, then its successor numbered n+1, also falls. Therefore, we conclude that all the dominoes will fall.
The argument above is the crux of induction. To prove a property over all natural numbers 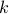 , we may argue as follows:
, we may argue as follows:
The property is true for
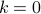 (the first natural number).
(the first natural number).If the property is true for some natural number
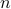 then it is true for natural number
then it is true for natural number 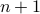 .
.
Example-1
Induction can be really useful to guess and prove closed forms of sequences. Consider a simple one:

We have 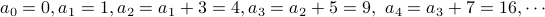 .
Therefore here is our guess:
.
Therefore here is our guess: 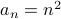 . How do we prove it?
. How do we prove it?
Claim: 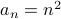 .
.
Proof is by induction on 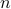 .
.
Base Case: We verify that
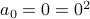 . So this works.
. So this works. Induction Hypothesis: For all
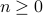 , If
, If 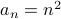 then
then 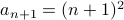 .
. Proof of induction hypothesis: Let
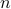 be any given natural number such that
be any given natural number such that 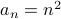 . We seek to prove that
. We seek to prove that 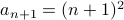 .
.
![begin{array}{rcll} a_{n+1} &=& a_n + (2 (n+1) - 1) & [mbox{Apply the recurrence relation}] &=& a_n + 2n + 1 & [mbox{Simpliciation} ] &=& n^2 + 2n + 1 & [ a_n = n^2, mbox{by induction hypothesis}] &=& (n+1)^2 end{array}](eqs/5737743573554049257-130.png)
Therefore, we have proved that 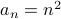 for all
for all  by induction.
by induction.
Example-2
Theorem The sum of first 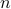 numbers
numbers 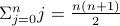 .
.
We prove this fact by induction just like we did for the dominoes.
Base Case: We will verify the fact for 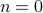 . Note that
. Note that 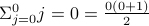 .
.
Inductive Hypothesis: For all  ,
If
,
If  , then
, then 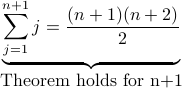 .
.
Proof of Inductive Hypothesis
Let 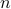 be any given natural number such that
be any given natural number such that  holds.
We wish to show
holds.
We wish to show

We note that
![begin{array}{rcll} Sigma_{j=0}^{n+1} j &=& left( Sigma_{j=0}^n j right) + (n+1) & [mbox{Peel off last term of the summation}] &=& frac{n(n+1)}{2} + (n+1) & [mbox{Assume the induction hypothesis}] &=& frac{n (n+1) + 2 (n+1)}{2} & [mbox{Algebra}] &=& frac{ (n+2)(n+1)}{2} end{array}](eqs/7596199233152566254-130.png)
Example 3
Let us try the sequence 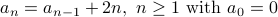 .
.
First, we guess what the closed form could be: 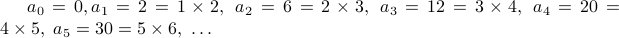 .
.
Claim  .
.
We prove by induction. The base case is for 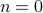 .
.
Base Case: For
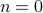 , we verify
, we verify 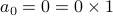 .
.
Inductive Hypothesis: For all
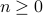 , If
, If 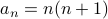 then
then 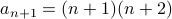 .
.
Weak Induction Proofs
We wish to prove a property 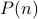 for all natural numbers
for all natural numbers 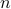 . I.e,
. I.e, 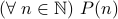 .
.
Proof by (weak) induction proceeds by establishing a base case:
Base Case: Verify that
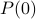 holds.
holds. Induction Hypothesis:
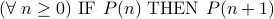 .
.
So far, we have been working with weak induction. We will now work with strong induction proofs.
Strong Induction Proofs
In weak induction, we prove that the number 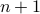 satisfies
satisfies 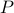 by assuming that
by assuming that 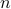 (its immediate predecessor) does. That may not always yield
the simplest proof.
(its immediate predecessor) does. That may not always yield
the simplest proof.
Example 1
The function 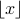 is also called the floor of
is also called the floor of 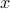 . It gives the smallest integer that is less than or equal to
. It gives the smallest integer that is less than or equal to 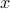 .
.
The function  is also called the ceil of
is also called the ceil of 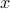 . It gives the smallest integer that is greater than or equal to
. It gives the smallest integer that is greater than or equal to 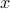 .
.
As examples, 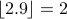 whereas
whereas 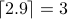 . For negative numbers, it is a little counter intuitive:
. For negative numbers, it is a little counter intuitive:
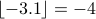 whereas
whereas 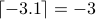 .
.
Consider the recurrence 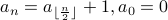 .
.
Here is the result of performing the recurrence on a few values of 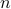 .
.
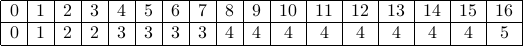
Some of you may recognize the pattern (it is rather important one for CS). Here is the guess: 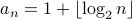 for
for  with
with 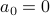 .
.
We can now try proving it by induction. We will first use weak induction.
Theorem For all  , If
, If  then
then 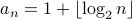 .
.
The theorem only applies to natural numbers  . We handle this by simply allowing the base case of induction to start at
. We handle this by simply allowing the base case of induction to start at 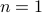 .
.
Failure of Proof by Weak Induction
Base-Case For 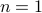 , we verify that
, we verify that 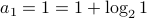 .
.
Inductive Hypothesis: 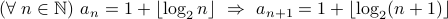 .
.
This is not easy to prove and infact is strictly not true. This is because 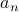 depends on
depends on 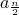 and not on
and not on 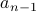 like our
previous sequences.
like our
previous sequences.
Proof by Strong Induction
Strong induction is different from weak in the inductive hypothesis.
Weak Induction: Assume
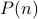 prove
prove 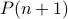 .
. Strong Induction: Assume
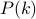 for all
for all 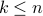 and prove
and prove 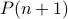 .
.
Going back to dominoes, we assume in weak induction that the 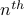 domino falls and prove that so does the
domino falls and prove that so does the 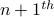 .
In strong induction, we assume that all dominoes numbered
.
In strong induction, we assume that all dominoes numbered 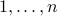 fall and prove that in that case the
fall and prove that in that case the 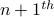 also falls.
also falls.
Claim: For all  , If
, If  then
then 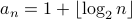 .
.
Proof is by strong induction over 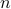 .
.
Base-Case For 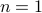 we verify that
we verify that 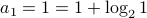 .
.
(Advanced note: For strong induction, the base case is really not needed but we will go through it for the sake of uniformity, anyway).
Strong Inductive Hypothesis:
For all  If
If 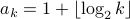 for all
for all 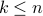 then
then 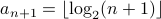 .
.
We will prove the strong induction hypothesis.
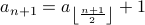
We will split this into two cases based on 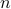 being odd or not.
being odd or not.
Case-1 Assume 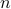 is odd, i.e,
is odd, i.e, 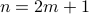 for some natural number
for some natural number 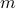 . Then
. Then  .
We have
.
We have
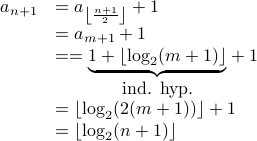
Case-2 Assume 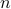 is even. I.e,
is even. I.e, 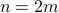 for some
for some 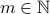 . Therefore,
. Therefore, 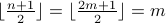 .
.
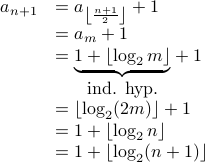
There is now an extra proof needed on the side that argues that whenever 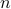 is even,
is even, 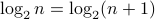 .
.
For completeness, here is the proof of the side claim.
Side-Claim: For all natural numbers  , if
, if 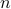 is even, then
is even, then  .
.
This is an example of a proof by contradiction.
Let us assume otherwise. I.e.,  and
and
 . In other words, we have
. In other words, we have

Since 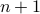 is odd, we cannot have
is odd, we cannot have 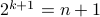 . Therefore,
. Therefore, 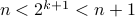 . As a result, there is a natural number between
. As a result, there is a natural number between 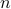 and
and 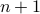 . This is a
contradiction. Therefore, it has to be the case that
. This is a
contradiction. Therefore, it has to be the case that  .
.