CSCI 2824: Lecture Notes # 6

In these notes, we are going to

Provide proofs of various propositions
Ask you to fix some of our proofs.
Practice proving theorems by expressing your argument in a succinct and logically consistent form.

Basic Proof Strategies

How to prove a theorem of course depends on what you are asked to prove. We will give you some templates for how a proof must proceed. Of course this works only for simple theorems. For complex theorems, the idea is to decompose into simpler claims. Proving the simpler claims, we build upon them to prove more complex claims and so on.

We will restrict ourselves to facts about numbers for now.

Universal Statements

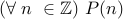
For every number , some fact holds over : (forall n in mathbb{Z}) P(n)

Proofs of Universal Statements

Universal statements are proved as follows:

Assume an arbitrary number .
Prove that 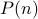will hold usually by doing some algebra.

Let us now look at an example.

Example #1

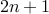Theorem For every natural number , the number 2 n +1 is an odd number.

Proof

Let be any given number and let .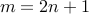
We are asked to show that 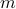is odd.
We will show therefore, that 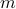leaves a remainder of 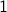when divided by .

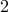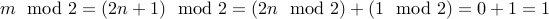
m mod 2 = (2 n + 1) mod 2 = (2 n mod 2) + (1 mod 2) = 0 + 1 = 1

QED.

Universal Statements With Implication

We now look at a special form of universal statements of the form:

Universal Statement With Implication

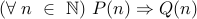(forall n in mathbb{N}) P(n) Rightarrow Q(n) .

Following the general rule for universal statements, we write a proof as follows:

Let be any given number in .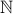
There are two cases 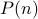does not hold or 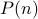holds.
In case 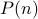does not hold, the implication trivially holds.
In case 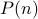holds, we will now prove .
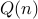- Typically, some algebra here to show that .

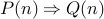We can use a simple short-cut that avoids unnecessary language in such proofs.

Let be any given number in 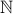such that 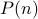holds.
We will show that under these assumptions 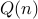holds.

- Typically, some algebra to show that 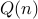holds.

Example #1

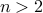Theorem If is an even number and n > 2 then is composite.

Proof

Here are our reasoning steps:

Assume a given number such that is even and .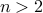
From this assumption, we can write 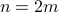wherein .
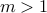- has two non-trivial factors 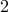and .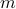
- is therefore composite. QED.

Example #2

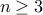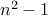Theorem For every natural number , If n geq 3 then n^2 -1 cannot be prime.

Proof

Here are the steps of our reasoning.

Assume a given number such that .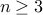
We will now show that 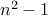is a composite number.
- By elementary algebra, we see that .
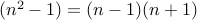- We note that 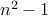can be written as the product of two numbers.
- It remains to show that the factors of 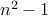are not trivial. That is, 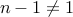( and therefore ).
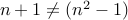  - Since 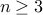, 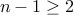. Therefore .
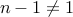- We have just shown that 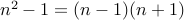and both 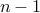is greater than 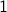. Therefore 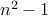is composite. QED.

Existential Statements

We will mention existential statements. They are rarer but interesting.

Simple existential statements assert that a number with some property exists.

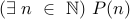(exists n in mathbb{N}) P(n) .

To prove an existential statement, we just give an example.

Example

Theorem There exist two prime numbers whose sum is also a prime number.

Proof

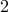and 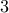serve as examples to our theorem.

Diversion: Constructive Proofs

Existential statements can be proved in another way without producing an example. Typically this involves a proof by contradiction (we will study these types of proofs soon). Such proofs are called non-constructive proofs.

Theorem There exist two irrational numbers and 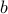such that 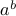a^b is rational.

Proof

We will show that such numbers exist without giving you a concrete example.

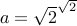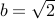Consider the number $a = sqrt{2}^{sqrt{2}}$ and b = sqrt{2} .

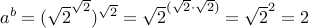
$a^b = (sqrt{2}^{sqrt{2}})^{sqrt{2}} = sqrt{2}^{(sqrt{2}cdot sqrt{2})} = sqrt{2}^2 = 2$

Therefore 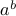a^b is rational. We know that 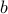is irrational.

There are two cases:

is irrational. In that case, we are done since 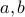are both irrational and 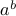is rational.
is rational.
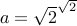1. In that case, $a = sqrt{2}^{sqrt{2}}$ is rational.
2. But 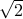is irrational itself.
3. So in this case, we have 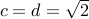are irrational and 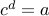is rational by assumption.

As a result, there must exist two numbers 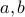a,b such that 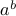a^b is rational while 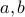a,b themselves are irrational. ( Our argument just has not produced any concrete example to point to. :-) )

QED.

Discuss some of the philosophical implications of constructivism vs. non-constructivism

Needless to say we will leave non-constructive proofs to mathematicians and the debate to the philosophers for now. If you are interested, these ideas are usually covered in a philosophy of mathematics or a philosophy of science class.

Flawed Mathematical Arguments

We will now see examples of flawed arguments that you need to watch out for when doing mathematics. Examples include

Proving by example: Just present a few examples and note that an universal statement holds based on these.
Assuming some fact in the proof that does not follow from the premise.
Proving by intuition: Appeal to your intuition usually by drawing a diagram.
Statements that should never be present in a good proof:
- it is clear to me (proof by vision!! )
- it just feels right (the touchy-feely proof!! )
- intuitively,… (proof by intuition!! )
- my professor told us that,… (proof by authority!! )
- it is obvious,.. (unless it truly truly truly is rather obvious as 1+1 = 2 !!).
Proving the wrong statement.
- Proof of the converse (instead of proving 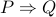, we prove ).
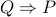- Proof of something unrelated.
Not proving the statement for all the cases.
- Missing out on some corner cases.
  - Proof only applies to even but not to odd.

Example# 1

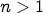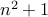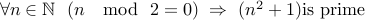Claim: For n > 1 , If is even n^2+1 is prime. I.e, $forall n in mathbb{N} (n mod 2 = 0) Rightarrow (n^2+1) mbox{is prime}$ .

Proof Attempt # 1

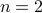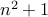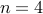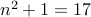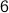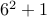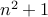Let us test for n=2 , we have n^2+1 is 5. Works. It also works for n=4 since n^2+1 = 17 is prime and since 6^2+1 is prime. Therefore, n^2 +1 is prime if is prime.

Let us attempt one more proof of this:

Proof Attempt # 2

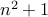Assume n^2+1 is prime. We will prove that must be even.

Since 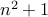is prime, and 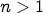, 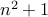must necessarily be odd.
Since 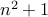is odd, it must be the case that 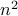is even.
If 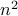is even, we have proved previously that is also even.
Therefore, is even. QED??

Are there any flaws in either of these proofs? Do they convince you of the truth of our “claim”?

Answer

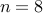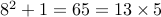The claim is false in the first place because it fails for n=8 , wherein 8^2+1 = 65 = 13 times 5 .

The first proof attempt is a proof by example which is generally invalid for universally quantified statements.

The second proof attempt actually sets out to prove the converse. Instead of proving 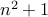n^2+1 is prime, it assumes this and tries to prove, instead, that is even.

Example #2

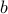Claim If two numbers and are odd, then 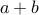a+b is even.

Exercise: Write this down in logical notation.

Let us look at a proof:

Attempted Proof

Proof Here are our reasoning steps:

Since is odd, it can be written as 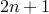for some .
Since 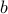is odd, it can be written as 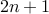too for some .
Therefore .
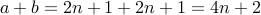But 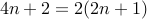is an even number.
Therefore, 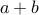is even. QED.

Is there anything wrong with the proof above?

Now let us look at a related claim:

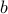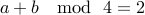Claim-2 If two numbers and are odd, then a+b mod 4 = 2 .

Is this a true statement?

Proof

Here are our reasoning steps:

Since is odd, it can be written as 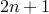for some .
Since 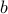is odd, it can be written as 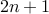too.
Therefore .
.
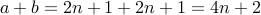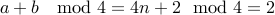Therefore, 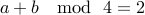. QED.

Can you correct the demonstrations above? What went wrong.

Answer

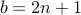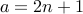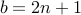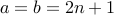The problem was in assuming that b = 2n +1 for some . By saying that a = 2n+1 , for some and b = 2n+1 for some , there is a flawed assumption that a = b = 2n+1 , which was never warranted.

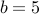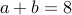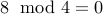Therefore, we are able to “prove” Claim-2, which is clearly false. For example, a=3 and b=5 yields us a+b = 8 and 8 mod 4 = 0 .

Claim-1 is correct and the corrected proof is as follows:

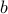Claim-1 If two numbers and are odd, then 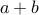a+b is even.

Corect Proof

Proof Here are our reasoning steps:

Since is odd, it can be written as 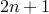for some .
Since 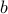is odd, it can be written as 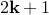too for some .
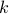Therefore .
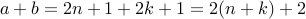But 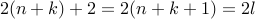is an even number.
Therefore, 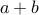is even. QED.

Example #3

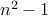Claim If is natural number then n^2-1 is a composite number.

Proof

Proof: Let be a natural number.

We can write 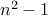as a product of .
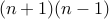Therefore 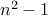is a composite number. QED??

Answer

The claim is actually false. Take 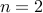n = 2 , we have 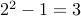2^2 - 1 = 3 , a prime number.

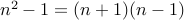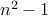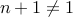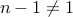What went wrong in the proof? Well, we are correct in writing as n^2 -1 = (n+1) (n-1) but this does not immediately show that n^2-1 is composite. We have to convince ourselves that n+1 not=1 and n-1 not = 1 . Recall:

Definition: Prime and Composite Numbers

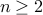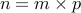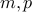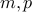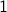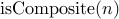A natural number n geq 2 is composite if it can be written as n = m times p for natural numbers m,p where m,p cannot be or itself. In logic, we define a predicate mbox{isComposite}(n) as follows:

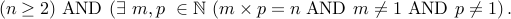(n geq 2) mbox{AND} (exists m,p in mathbb{N} ( m times p = n mbox{AND} m not= 1 mbox{AND} p not= 1),. .

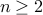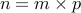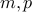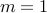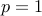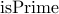Likewise, natural number n geq 2 is prime if n = m times p for some natural numbers m,p , then m= 1 or p= 1 . In logic, we define a predicate mbox{isPrime} for natural numbers, as follows:

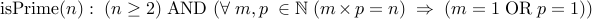
mbox{isPrime}(n): (n geq 2) mbox{AND} (forall m,p inmathbb{N} ( m times p = n) Rightarrow ( m = 1 mbox{OR} p = 1) )

An important exception involves the numbers 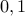0,1 . These are taken to be neither prime nor composite.

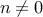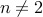The proof above can only be correct when n not = 0 and n not = 2 .