Discrete Structures (CSCI 2824, Spring 2014)
The Amazing Binary World
In this lecture, we will consider some basics of the binary number system and representing numbers inside a computer.
Place Valued Number Systems
A decimal number n=1092991367 is quite familiar and seems quite natural to us. This is most probably because ancient humans used the fingers in their hands to count and convey numbers to each other. For example, we have learnt in high school that the number ’'n’’ above is odd (not divisible by 2), leaves a remainder of 2 when divided by 3, is not divisible by 5 and so on.
On the other hand, what can we say about the number ’’1001001’’? Is it odd or even? Is it divsible by 3? How about 5? Binary numbers are not easy to handle mentally, even for experienced computer scientists, unless one has worked with them for a long time. With the advent of digital computers, it became much more easier to deal with bits inside a computer that could either be ’'on’’ or ’'off’’ conveying a 1 or a 0. Therefore, the use of binary numbers is quite prevalent in computer arithmetic. It is hard to imagine doing things any other way.
As the joke goes: there are 10 people on earth, those who understand binary and those who do not.
Binary Number
Let us first consider whole numbers and ignore fractions. A binary number is a string of 0s and 1s. Generally, we remove the leading zeros and simply write starting from the first 1 bit. In other words the number 0000111 is the same as 111. We sometimes write the base of the number as a subscript to resolve ambiguities.
Eg., 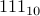 is the number one hundred and eleven to the base 10, which is entirely different from
is the number one hundred and eleven to the base 10, which is entirely different from 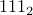 , which is in fact
, which is in fact 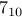 .
Examples of binary numbers:
.
Examples of binary numbers:
1000110
10101
11
1
0
The leftmost bit of a number is called its most significant bit. The rightmost bit is called the least significant bit. Can you guess why these bits are called so?
We can convert binary numbers to decimals rather easily. Take the
number 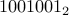 . Its value in decimal can be found by the
following procedure:
. Its value in decimal can be found by the
following procedure:
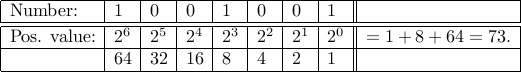
Here are some decimal numbers corresponding to binary numbers:
| Binary | Decimal |
| 0 | 0 |
| 10 | 2 |
| 11 | 3 |
| 1111 | 15 |
| 11110 | 30 |
| 1010 | 12 |
Converting Decimal to Binary
To convert a decimal number to binary involves the following procedure that outputs starting from the least significant bit to the most.
If n is zero or one then output 0 or 1, respectively, and exit.
If n is odd then output a 1 and set
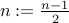 . REPEAT the entire procedure for the new n.
. REPEAT the entire procedure for the new n.If n is even then output a 0 and set
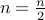 . REPEAT the entire procedure for the new n.
. REPEAT the entire procedure for the new n.
Here is some C code:
void convertToBinary(int n){ int result[64]; int nBits = 0; if ( n < 0) { /* Input is negative */ printf("- "); n = -n; } if (n == 0){ printf ("0"); return; } while ( n > 0){ /* Check <span class="statement">if</span> n is even or odd. You can instead write result[nBits] = n%2; */ if (n % 2 == 0){ result[nBits] = 0; } else { result[nBits] =1; } nBits ++; n = n/2; /* Divide by 2 */ } /* Print starting from the end */ for (i = nBits -1; i >= 0; i --){ printf ("%d", result[i]); } printf ("\n"); }
Eg., Consider the number n = 161 in decimal. Here are the steps:
n is odd, therefore, we output a 1 and set n = 80.
n is now even, therefore output a 0 and set n = 40.
n is now even, therefore output a 0 and set n = 20.
n is even, therefore output a 0 and set n = 10.
n is even, therefore output a 0 and set n = 5.
n is odd, therefore output a 1 and set n = 2.
n is even, output a 0 and set n = 1
n =1 so output a 1 and EXIT.
Therefore 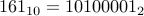 .
.
Some Binary Tricks
Now let us try to answer the following questions:
How can we say if a given binary number is divisible by 2?
Just check if the last bit is zero.
How can we say if a given binary number is divisible by 4?
Just check if the last two bits are zero.
How can we say if a given binary number is divisible by 3?
We will explain a procedure below.
How can we say if a given binary number is divisible by 10?
We will present the trick in class and do the analysis using modular arithmetic later on.
Binary Divisibility by 3 Check
Take any number in binary say 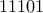 . To test if it is divisible by three,
. To test if it is divisible by three,
We add together all the odd bits and all the even bits as if they were decimal numbers.
In this case the odd bits are
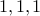 summing up to
summing up to 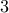 and the even bits are
and the even bits are 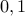 summing up to
summing up to 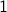 .
.Subtract the sum of odd bits from that of even bits. In this case we get
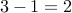 .
. If the result is divisible by
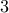 then so is the original number. In this case,
then so is the original number. In this case, 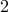 is not so the original number is not.
is not so the original number is not.
Some examples are worked out below:
| Number | Sum of Odd Bits | Sum of Even Bits | Divisible By 3 ? | |
| 11 | 1 | 1 | Yes | |
| 1001 | 1 | 1 | Yes | |
| 10011 | 2 | 1 | No | |
| 111010101 | 5 | 1 | No |
We will show why this trick works when we do modular arithmetic. Then we will also be able to tackle divisibility by 5, 7 and 11 as well :-)
Binary fractions
Just as we are able to represent fractions in decimals, we are also able to represent binary fractions. A binary fraction is written as
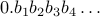 . We can of course have whole numbers plus fractions just like we do for decimal numbers. The point used here
will be called the radix point or sometimes confusingly people call it the decimal point.
. We can of course have whole numbers plus fractions just like we do for decimal numbers. The point used here
will be called the radix point or sometimes confusingly people call it the decimal point.
Again, the first bit after radix point represents 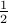 , the second bit represents
, the second bit represents 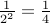 , the third bit represents
, the third bit represents 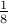 and so on.
and so on.
Let us again give some examples:
| Binary | Decimal | |
| 0.111 | 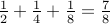 | |
| 0.0001 | 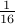 | |
| 0.10101 | 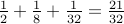
|
Now, a natural question is how do we represent fractions like 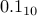 or
or 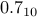 in binary. Turns out that we cannot quite represent
in binary. Turns out that we cannot quite represent 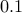 in finitely many bits.
In fact we have
in finitely many bits.
In fact we have 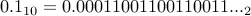 . Note that it has a
. Note that it has a 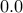 followed by an infinitely repeating pattern of
followed by an infinitely repeating pattern of 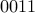 at the end.
at the end.
Likewise 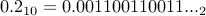 is an infinitely repeating sequence of
is an infinitely repeating sequence of 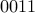 after the radix point.
after the radix point.
We have seen this situation in decimal as well. For example 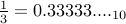 is an infinitely repeating sequence of
is an infinitely repeating sequence of 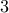 s.
s.
What if we truncate the binary expansion of 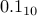 after say
after say 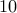 bits? We then have a number such as
bits? We then have a number such as 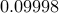 (not the exact value) that is close to
(not the exact value) that is close to 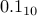 but not quite
but not quite 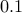 . In fact, the standard float used in most programming language is able to represent up to
. In fact, the standard float used in most programming language is able to represent up to 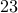 bits of a binary fraction.
The rest of it is simply truncated off.
bits of a binary fraction.
The rest of it is simply truncated off.
Arithmetic Error in Computers
Does it really matter that a 0.1 inside a computer is really 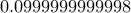 ?
In some cases it does.
?
In some cases it does.
Sigfried Rump pointed out the following dramatic example:
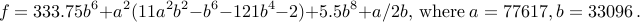
Here is a C program to compute  :
:
#include <stdio.h> float a = 77617; float b = 33096; int main(){ float f = 333.75 * b*b*b*b*b*b + a*a * ( 11 * a*a * b*b - b*b*b*b*b*b - 121 * b*b*b*b -2) + 5.5 * b*b*b*b*b*b*b*b + a/(2 * b) ; printf("f = %f \n", f); return 1; }
When run on a 64 bit intel we get f = -44450695952321879337122922496.000000. That seems pretty good. But in reality, the answer
should be 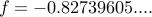 . In other words, the answer computed on my desktop is off by a factor of
. In other words, the answer computed on my desktop is off by a factor of 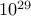 !!!
!!!
Floating point errors due to finite binary arithmetic is a fact in life and arises because fractions can have infinitely long binary expansions and computers can only represent a finite (small) part of this.