Lecture 18 : One-to-One and Onto Functions.
In this lecture, we will consider properties of functions:
Functions that are One-to-One, Onto and Correspondences.
Proving that a given function is one-to-one/onto.
Comparing cardinalities of sets using functions.
One-to-One/Onto Functions
Here are the definitions:
 is one-to-one (injective) if
is one-to-one (injective) if  maps every element of
maps every element of 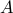 to a unique element in
to a unique element in 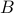 . In other words no element of
. In other words no element of 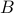 are mapped to by two or more elements of
are mapped to by two or more elements of 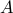 .
. 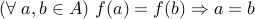 .
.
 is onto (surjective)if every element of
is onto (surjective)if every element of 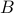 is mapped to by some element of
is mapped to by some element of 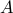 . In other words, nothing is left out.
. In other words, nothing is left out. 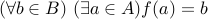 .
.
 is one-to-one onto (bijective) if it is both one-to-one and onto. In this case the map
is one-to-one onto (bijective) if it is both one-to-one and onto. In this case the map  is also called a one-to-one correspondence.
is also called a one-to-one correspondence.
Example-1
Classify the following functions 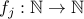 between natural numbers as one-to-one and onto.
between natural numbers as one-to-one and onto.
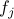 | One-to-One? | Onto? |
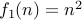 | Yes | No |
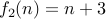 | Yes | No |
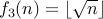 | No | Yes |
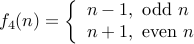 . . | Yes | Yes |
It helps to visualize the mapping for each function to understand the answers.
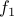 is not onto because it does not have any element
is not onto because it does not have any element  such that
such that 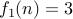 , for instance.
, for instance.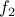 is not onto because no element
is not onto because no element  such that
such that 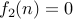 , for instance.
, for instance.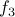 is not one-to-one since
is not one-to-one since 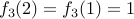 .
.
Example-2
Prove that the function 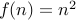 is one-to-one.
is one-to-one.
Proof: We wish to prove that whenever 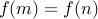 then
then 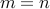 . Let us assume that
. Let us assume that 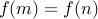 for two numbers
for two numbers 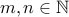 . Therefore,
. Therefore,
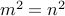 . Which means that
. Which means that 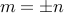 . Splitting cases on
. Splitting cases on  , we have
, we have
For
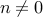 ,
, 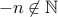 , therefore
, therefore 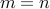 for this case.
for this case. For
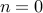 , we have
, we have 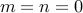 .
Therefore, it follows that
.
Therefore, it follows that 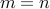 for both cases.
for both cases.
Example-3
Prove that the function 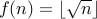 is onto.
is onto.
Given any 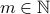 , we observe that
, we observe that 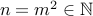 is such that
is such that 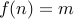 . Therefore, all
. Therefore, all 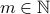 are mapped onto.
are mapped onto.
Claim-1 The composition of any two one-to-one functions is itself one-to-one.
Let 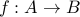 and
and 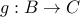 be both one-to-one. We wish to tshow that
be both one-to-one. We wish to tshow that 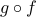 is also one-to-one.
is also one-to-one.
Assume that
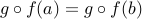 for two elements
for two elements  .
. Therefore
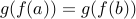 .
. Since
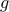 is itself one-to-one, it follows that
is itself one-to-one, it follows that 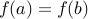 .
. Since
 is one to one and
is one to one and 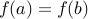 it follows that
it follows that 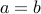 .
. Therefore
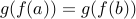 can happen only if
can happen only if 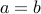 .
.
The reasoning above shows that 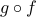 is one-to-one.
is one-to-one.
Claim-2 The composition of any two onto functions is itself onto.
Let 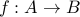 and
and 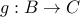 be onto functions. We will prove that
be onto functions. We will prove that 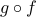 is also onto.
is also onto.
Let
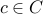 be any element.
be any element. Since
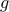 is onto, we know that there exists
is onto, we know that there exists 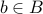 such that
such that 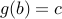 .
.Likewise, since
 is onto, there exists
is onto, there exists 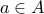 such that
such that 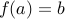 .
.Combining,
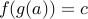 .
. Thus,
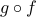 is onto.
is onto.
Comparing Cardinalities of Sets
Let 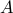 and
and 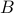 be two finite sets such that there is a function
be two finite sets such that there is a function 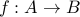 . We claim the following theorems:
. We claim the following theorems:
If
 is one to one then
is one to one then 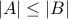 .
.If
 is onto then
is onto then 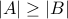 .
.If
 is both one-to-one and onto then
is both one-to-one and onto then 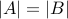 .
.
The observations above are all simply pigeon-hole principle in disguise.
Theorem Let 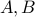 be two finite sets so that
be two finite sets so that 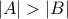 . Any function from
. Any function from 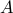 to
to 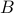 cannot be one-to-one.
cannot be one-to-one.
Let 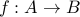 be any function. Think of the elements of
be any function. Think of the elements of 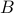 as the holes and elements of
as the holes and elements of 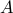 as the pigeons. There are more pigeons than holes. Therefore two pigeons have to share (here map on to) the same hole.
as the pigeons. There are more pigeons than holes. Therefore two pigeons have to share (here map on to) the same hole.
QED.
We now prove the following claim over finite sets  .
.
Claim Let 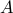 be a finite set. Prove that every one-to-one function
be a finite set. Prove that every one-to-one function 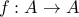 is also onto.
is also onto.
We will prove by contradiction.
Let
 be a one-to-one function as above but not onto.
be a one-to-one function as above but not onto. Therefore,
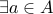 such that for every
such that for every 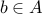 ,
, 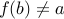 .
. Therefore,
 can be written as a one-to-one function from
can be written as a one-to-one function from 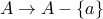 (since nothing maps on to
(since nothing maps on to 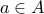 ).
).Similarly, we repeat this process to remove all elements from the co-domain that are not mapped to by
 to obtain a new co-domain
to obtain a new co-domain 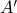 .
. is now a one-to-one and onto function from
is now a one-to-one and onto function from 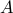 to
to 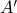 .
.However,
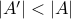 . Therefore by pigeon-hole principle
. Therefore by pigeon-hole principle  cannot be one-to-one.
cannot be one-to-one.
The last statement directly contradicts our assumption that  is one-to-one.
QED.
is one-to-one.
QED.
Infinite Sets
We now note that the claim above breaks down for infinite sets.
Let us take 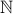 , the set of all natural numbers.
, the set of all natural numbers.
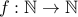 defined by
defined by 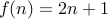 is one-to-one.
is one-to-one.However,
 is not onto.
is not onto.
Hilbert's Hotel
Consider a hotel with infinitely many rooms and all rooms are full.
An important guest arrives at the hotel and needs a place to stay. How does the manager accommodate the new guests even if all rooms are full?
Each one of the infinitely many guests invites his/her friend to come and stay, leading to infinitely many more guests. How does the manager accommodate these infinitely many guests?
One-to-One Correspondences of Infinite Set
There is a one to one correspondence between the set of all natural numbers 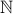 and the set of all odd numbers
and the set of all odd numbers 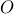 .
.
Take 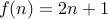 , where
, where 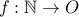 .
We note that
.
We note that  is a one-to-one function and is onto.
is a one-to-one function and is onto.
Can we say that 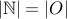 ? Yes, in a sense they are both infinite!! So we can say
? Yes, in a sense they are both infinite!! So we can say 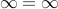 !!
Therefore we conclude that
!!
Therefore we conclude that
There are “as many” even numbers as there are odd numbers?
There are “as many” positive integers as there are integers? (How can a set have the same cardinality as a subset of itself? :-)
There are “as many” prime numbers as there are natural numbers?
Note that “as many” is in quotes since these sets are infinite sets.
Infinite Sets
There are many ways to talk about infinite sets. We will use the following “definition”:
A set 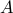 is infinite if and only if there is a proper subset
is infinite if and only if there is a proper subset 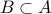 and a one-to-one onto (correspondence)
and a one-to-one onto (correspondence) 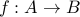 .
.
Here are some examples of infinite sets:
Natural numbers
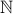 : The odd numbers
: The odd numbers 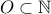 . We just proved a one-to-one correspondence between natural numbers and odd numbers.
. We just proved a one-to-one correspondence between natural numbers and odd numbers. Integers
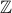 are an infinite set. The correspondence
are an infinite set. The correspondence 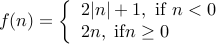 .
. Rational numbers
 : We will prove a one-to-one correspondence between rationals and integers
: We will prove a one-to-one correspondence between rationals and integers 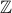 next class.
next class.