CSCI 2824: Lecture 22 Notes
Combinatorics
Combinatorics is the mathematics behind counting discrete structures. Often, it is important to know how many objects of a particular type exist to make some decisions. Eg.,
How many routes exist between two nodes in a network?
How many steps does a program take to run on an input of size n?
How many solutions exist for a particular constraint problem?
and so on…
In this module (Chapter 5 of the book), we will study the basics of counting objects. We will start from some basic puzzles.
Puzzle
We have three envelopes colored red, green and violet. We could invite one of three people Alice, Bob and Carol.
How many possible ways are there of choosing a person and a color for their invitation?
There are 9 possible ways. To understand why, we will construct a concept of choice-set. This set will represent the set of all the possible choices we have. In this case, our choices are
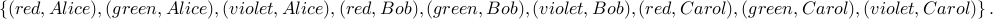
We have 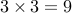 choices.
choices.
Constructing a choice set is very tedious, and often impossible. We would like to count directly, without actually constructing each choice separately.
Puzzle
We have three tee shirts. Two are red (indistinguishable) and one is violet. We have three people interested in these tee-shirts: Alice, Bob and Carol.
How many possibilities ways are there of choosing a color for every person?
Let us just enumerate possibilities.
Alice, Bob: Red, Carol: Violet
Alice, Carol: Red, Bob: Violet
Carol, Bob: Red, Alice: Violet.
There are three in all.
Another way to represent it is to use the notion of a choice set. If we choose who gets the violet shirt, the other two have to get the red (there is no choice for these two). Therefore choice set is
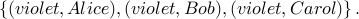
Puzzle
Let us say that CU, Nebraska and Texas are contending for the basketball playoffs in a round-robin. Each team needs to play the other exactly once. How many games will be there?
We know that two of the games will have CU in it. This leaves one game with Nebraska and Texas. So we arrive at 3 games in all.
Puzzle
There are 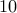 teams that need to play each other in a
tournament. Each team needs to play the other exactly once. How many
games will be played?
teams that need to play each other in a
tournament. Each team needs to play the other exactly once. How many
games will be played?
Let us number the teams 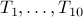 .
.
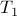 needs to play
needs to play 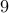 games.
games.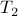 plays
plays 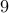 games but we already counted one against
games but we already counted one against 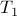 , so that leaves
, so that leaves 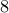 more games.
more games.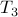 plays
plays 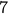 more games (we discount its games against
more games (we discount its games against 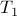 and
and 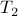 ).
).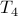 plays
plays 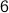 more games.
more games.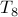 plays one more game.
plays one more game.We have already counted all the games that
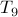 will play.
will play.
Total
Basic Rules for Counting
When asked to count the number of possibilities, we need to be careful of two things:
Do not double count a possibility.
Do not skip some possibility.
In the former case, our count will be larger than what it should be. In the latter case, the count will be smaller. If we commit both types of errors, the count may as well be a random number!!
Product Rule
Let us say that we have to choose 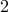 items, in order. There are
items, in order. There are 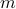 choices for item 1 and independently there are
choices for item 1 and independently there are  choices for item
2. Then there are
choices for item
2. Then there are 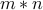 choices for both together.
choices for both together.
Let us revisit the first example:
We have three envelopes colored red, green and violet. We could invite one of three people Alice, Bob and Carol.
How many possible ways are there of choosing a person and a color for their invitation?
There are two items: We need to choose (a) person amongst Alice, Bob and Carol and (b) color among red, green and violet. Therefore 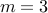 and
and 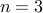 .
The number of possibilities is
.
The number of possibilities is 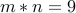 .
.
Puzzle
Tom, Mary and Francois go to an avant garde french restaurant. For their dessert, they have a choice between three things:
A: Creme Brulee,
B: Confiture de drole Canard aux tarte tatin and
C: Tarte aux fruits de mer et pomme de terre de Lorraine
How many possible ways are there of placing an order?
Puzzle
Let us say we have work to do in Paris, Bangkok or Budapest. There are Brian and Carla to send out. How many possible ways are there to send at most one person to one place?
Let us take it from the point of view of the person. There are three
options for Brian. Once we fix that, there are two remaining places
that Carla could go to. This gives us 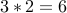 options.
options.
Puzzle
Let us take the previous puzzle, where we have 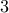 places: Paris, Bangkok or Budapest and
places: Paris, Bangkok or Budapest and 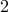 personnel (forget their names now). We do not care which person goes to which place.
personnel (forget their names now). We do not care which person goes to which place.
In other words, sending Brian to Paris and Carla to Bangkok is now the same as sending Carla to Paris and Brian to Bangkok. In this problem, we just care about which places get visited.
How many possibilities are there now?
Since there are just two people, one place has to be left out. There are three ways to choose this place, and therefore, three possible choices.
Puzzle
How many 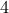 digit numbers can be formed by the numerals
digit numbers can be formed by the numerals 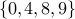 .
There are four digits
.
There are four digits 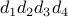 .
.
How many options are there for
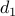 ? Note that a number cannot start with a zero (that makes it 3 digits).
? Note that a number cannot start with a zero (that makes it 3 digits).What about
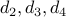 ?
?
Combine these to conclude that there are 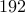 such numbers.
such numbers.
Permutations
Let us take  distinct objects
distinct objects 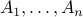 . A permutation of
. A permutation of 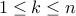 objects consists of choosing an ordered sequence of
objects consists of choosing an ordered sequence of 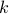 objects from the
objects from the  objects.
objects.
We cannot repeat objects.
Order in which we select matters. It matters what object we select first, what we select next and so on.
Example
List all permutations of two elements from the set 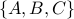 . The elements are
. The elements are 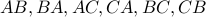 giving rise to six permutations of
giving rise to six permutations of 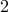 objects.
objects.
Example-1
List all permutations of all the 4 words in the phrase “University Of Colorado Boulder”. Note that in a permutation, (1) we cannot repeat objects and (2) order in which we place object matters.
“University of Colorado Boulder”
“University Boulder of Colorado”
“Colorado University of Boulder”
“Of Boulder Colorado University”
“University of Boulder Colorado”
“Of Colorado Boulder University”
“Boulder of Colorado University”
Looks like too many here. Let us reason this out formally: After rearrangement the new phrase is going to be:
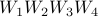
We have 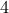 choices for
choices for 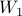 . Once we fix that we have
. Once we fix that we have 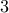 choices for
choices for 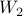 ,
, 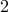 for
for 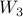 and the remaining goes to
and the remaining goes to 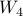 .
This gives rise to
.
This gives rise to 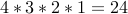 options.
options.
Example
Let us modify the previous example to require a phrase of 3 words (instead of all 4) from the set { University, Colorado, Of, Boulder }.
Formal Rules for Counting
We will now start to understand the intuition we have developed more precisely.
Basic Rules for Counting
Rule of products: If 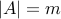 and
and 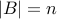 then
then 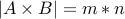 .
.
Example-1
We have 3 tee shirts with colors { red, green, blue } and 2 caps with labels {A,B}. How many possible ways are there of choosing a tee shirt and a cap?
Example-2
Let us say that in a tournament teams A, B and C play matches against each other in a round robin. How many matches are played?
How many possible outcomes are there for the tournament?
To count matches is easy, we know that there are three matches to be played M1: A vs. B, M2: A vs. C and M3: B vs. C.
Each match has two outcomes. Winner1 = {A,B}, Winner2 = {A,C}, Winner3 = {B,C}. Therefore, applying the product rule are 2 2 2 = 8 outcomes overall.
Rule of Sums
Rule of sums: If 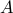 and
and 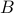 are disjoint then
are disjoint then 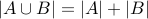 .
.
Example-1
We are allowed to make up a positive integer from the digits {1,3,5,7}. Each digit is to be used at most once (we may decide to skip a digit).
example of legal digits are: 13, 1, 3, 137, 7135, ….
Solution We split the problem into 4 disjoint counts: count all one digit numbers, two digit numbers, three digit and four digit numbers that can be formed. Together, using the rule of sums, we can simply add these counts and get the required overall count.
One digit numbers: 4 possible choices.
Two digit numbers:
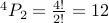 possible choices.
possible choices.Thee digit numbers:
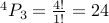 possible choices.
possible choices.Four digit numbers:
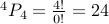 possible choices (remember
possible choices (remember 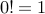 ).
).
Adding them up we have 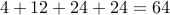 possible numbers.
possible numbers.
Rule of Complements
Recall that 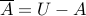 for a set
for a set 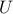 where
where 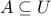 .
.
Rule of complements Let us say that instead of counting 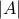 , we can count
, we can count 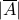 . Then
. Then 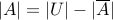 .
.
Example
How many odd numbers are there between 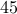 and
and 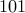 (include both limits in your count).
(include both limits in your count).
First let us just count the even numbers 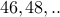 . Why?
. Why?
46 -> 1 even number
48 -> 2 even numbers
50 -> 3 even numbers
n ->
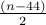 even numbers.
even numbers. 100 ->
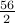 = 28 even numbers.
= 28 even numbers.
There are a total of 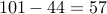 numbers between
numbers between 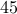 and
and 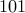 .
.
Therefore, odd number count is 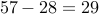 .
.
Example
Let us say we toss a coin ten times. Each time we toss, we get a head or a tail.
How many possible outcomes are there for the ten tosses?
How many outcomes are there where we see two heads in succession or two tails in succession?