Lecture 23: Permutations

We looked at permutations last class. Let us spell things out a little more.

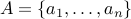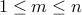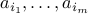Take a set $A = {a_1,ldots,a_n}$ with elements. A permutation of 1 leq m leq n elements is a sequence of elements $a_{i_1},ldots,a_{i_m}$ of 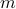distinct elements chosen from :

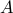No element can be chosen twice.
The order in which we choose the elements matter.

Eg., What are all the permutations of 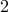elements chosen from the set 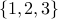{1,2,3} . Answer:

1,2
2,1
1,3
3,1
2,3
3,2 This gives rise to 6 permutations.

The number of permutations of 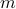elements chosen from a set of elements is denoted ${}^nP_m$ .

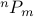What is the number 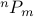${}^nP_m$ ?

choices for the first element in the permutation.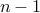
choices for the second.
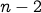for the third.
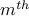choices for the $m^{th}$ element.

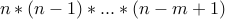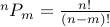That gives us by product rule n * (n-1) * ... * (n-m+1) choices overall. We can write the number above as ${}^nP_m = frac{n!}{(n-m)!}$ .

Example

How many 4 digit numbers can we form from the digits {1,2,3,7,9}, where we need to use each digit precisely once?

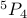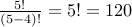In other words we are looking for a permutation of 4 elements from a set with 5 elements. The answer is ${}^5P_4$ which is $frac{5!}{(5-4)!} = 5! = 120$ .

Example

How many four digit numbers can be formed wherein (a) the digits in {1,2,3,7,9} are never used or (b) if some digit is used it is used multiple times.

Wierd problem? But can you find a connection between what is asked in Example Often looking at the complement of a set that we need to count can be easier. :-)

Example

Let 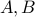A,B be two sets where 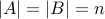|A| = |B| = n . How many one-to-one correspondences can exist between 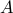and ?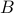

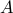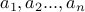Answer: Let us write to be ${a_1,a_2...,a_n}$ . Let 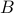be the set ${b_1,...,b_n}$ .

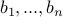Choose a permutation of all the elements of .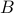
Once the permutation is chosen, link 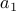to the first element in the permutation, 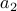to second,…, 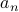to the $n^{th}$ .

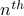Each one-to-one correspondence can be formed in this manner.

Therefore

Therefore there are 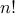functions.

Question: Let us say professor X says that this is the wrong way to do this. He objects that we did not permute 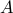. So in his technique:

We take each permutation of 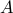, each permutation of 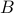and link the corresponding elements of the permutations. Thus, he reasons that there should be 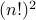one-to-one correspondences.

What is the flaw in his argument?

Combinations

We will now talk about combinations. Note that in permutations the order in which we choose things matter. When doing combinations the order does not matter.

A choice of 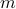elements out of a set with elements is one where

1. we choose 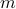elements (by definition, no element can be chosen twice).
2. the order in which we choose things do not matter.

We say that the number of such choices is 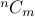${}^nC_m$ (say it as choose ).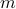

Let us try some examples.

Example

Take the set A ={1,2,3,5}. How many ways are there of choosing a subset with 2 elements?

Obviously, in a subset, we do not care if we choose {1,2} or {2,1} they are the same subset.

Let us first write down the permutations of 2 elements

1,2 and 2,1
1,3 and 3,1
1,5 and 5,1
2,3 and 3,2
2,5 and 5,2
3,5 and 5,3

Now notice that the number of choices in our problem is exactly half the number of permutations.

Since {1,2} is the same as {2,1}

{1,3} is the same as {3,1} and so on.

So the answer should be 6.