Introduction to Theory of Computation (CSCI 3434/5444, Fall 2015)
Class Timings: TTh (5:00 - 6:15 PM)
Class Location: ECCR 265.
Instructor: Sriram Sankaranarayanan
Pre-Requisites: Calculus I,II, Data Structures (CSCI 2270), Discrete Structures (CSCI 2824) and Algorithms (CSCI 3104).
Office Hours: We will have the following hours:
Agile office hours before class on TTh. Instructor will arrive half an hour early and stay back to answer questions.
Tuesdays 1:30 - 2:30 PM and Thursdays 2 - 3PM.
Oct 1st, 2015 First in-class quiz.
Aug 17, 2015 Please signup on moodle.
Aug 15, 2015 Course page is live!
Assignments
All assignments will be posted on moodle. Your identitykey is needed for signing in.
Lecture Schedule and Notes
The schedule of lectures shown below is subject to change. We will post lecture notes for most topics and videos for selected topics. We will strive to post all material well in advance. Please take a look through them, and come prepared for class.
| ID | Date | Topics Covered | Book Sections |
| 1 | Aug 25 | Introduction: Languages and Motivations for this class. | Chapter 0 |
| 2 | Aug 27 | Finite State Machines: Regular languages, deterministic and nondeterministic finite state machines | 1.1, 1.2 |
| 3 | Sep 1 | Aleks Chakarov Guest Lecture Nondeterministic machines: subset construction, regular expressions | 1.2, 1.3 |
| 4 | Sep 3 | Aleks Chakarov Guest Lecture Equivalence of regular expressions and finite automata | 1.3 |
| 5 | Sep 8 | Closure properties of regular languages, pumping lemma | 1.4 |
| 6 | Sep 10 | Wrap up for regular languages | |
| 6 | Sep 15 | Context Free Languages: Grammars and derivations | 2.1 |
| 7 | Sep 17 | Pushdown machines | 2.2 |
| 8 | Sep 22 | Aleks Chakarov Guest Lecture Noncontext free grammars and deterministic CFLs | 2.3 |
| 10 | Sep 24 | Aleks Chakarov Guest Lecture Closure properties of CFLs | |
| 11 | Sep 29 | Wrapup of CFLs | |
| 12 | Oct 1 | In class quiz and start Turing Machines | 3.1 |
| 13 | Oct 6 | Turing Machine Variants: Recursive vs. Recursively Enumerable Sets | 3.2, 3.3 |
| 14 | Oct 8 | Decidability: Decidable Languages | 4.1 |
| 15 | Oct 13 | Halting Problem: Diagonalization, Reductions | 4.2 |
| 16 | Oct 15 | Reductions: More undecidable problems | 5.1, 5. 2 |
| 17 | Oct 20 | Logics and Decidability | 6.2 |
| 18 | Oct 22 | Wrap up of Turing Machines and Decidability | |
| 19 | Oct 27 | Quiz # 2 & Start Complexity | 7.1,7.2 |
| 20 | Oct 29 | NP, co-NP with examples. Polynomial time reduction and NP-completeness | 7.3 |
| 21 | Nov 5 | NP-complete problems and reductions | 7.4 |
| 22 | Nov 10 | Wrap up of NP-completeness | |
| 23 | Nov 12 | Space Complexity Classes: Savitch's theorem | 8 |
| 24 | Nov 17 | co-NL and NL problems | |
| 25 | Nov 19 | Quiz # 3 & PSPACE and PSPACE-complete problems | |
| 26 | Dec 1 | Special Topics: TBA |
Course Objectives
The course aims to provide an introduction to the mathematical theory of computation: a subject that current CS undergraduates do not routinely encounter. The key course objectives are as follows:
Understand models of computation including finite state machines, pushdown machines, and Turing machines.
Understand applications to pattern matching, parsing, natural language processing and programming languages.
Understand the Church-Turing thesis and the existence of undecidable languages.
Learn classic results on complexity classes including P and NP.
Use reductions to prove NP completeness of problems.
Understand why P vs. NP question has remained unresolved for nearly 50 years now!
Topics Covered
Roughly, we will cover the following topics (some of them may be skipped depending on the time available).
Regular Languages.
Finite State Machines.
Nondeterminism.
Regular expressions.
Closure properties.
Pumping lemma: nonregular languages.
Context Free Languages (CFL).
Context Free Grammars (CFG) and derivations.
Pushdown automata (PDA): deterministic and nondeterminstic PDAs.
Closure Properties.
Pumping Lemma for CFLs.
Applications (Parsing).
Turing Machines and Computability Theory.
Turing Machines and the Church-Turing Thesis. Formal definition of an algorithm.
Decidability and undecidability: recursive enumerable and recursive languages.
Halting problem and reductions.
Post's correspondence problem.
The classical decision problem (entscheidungsproblem) and decidability of logical theories.
Arithmetic heirarchy.
Polynomial Time and Nondeterministic Polynomial Time.
The complexity classes P and NP.
Polynomial time reductions.
Cook-Levin Theorem: NP-completeness of 3-SAT.
Reductions to NP complete problems.
Resource Bounded Turing Machines and Complexity Classes.
Time and Space bounded machines, complexity classes.
The complexity classes: NL, PSPACE, EXPTIME and NEXPTIME.
Savtich's and Immerman–Szelepcsényi theorems.
The polynomial hierarchy.
Advanced Topics:
Reactive computation:
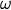 -automata.
-automata.Timed and hybrid automata.
Quantum computation.
Textbook
We will primarily use the textbook by Michael Sipser:
Introduction to the Theory of Computation, Michael Sipser. (2nd or 3rd edition).
Since we will not be covering deterministic context free languages in this class, the second edition of the book is sufficient for this class.
Course Work
We will have weekly assignments that will be based on the assigned reading for each class.
Pre-Lecture Work
Before you attend each lecture, we hope that you will spend 10-15 minutes to prepare:
Read the required portion of the book (at least skim through the book or notes provided).
Watch any videos posted (instructions will be sent via email).
Forums
We will set up forums that will allow students to interact with the course staff and with each other. You can participate in the forum and help answer questions posed by your classmates. Doing so counts towards your course participation score.
Weekly Assignments
We will assign weekly homework problem sets. Each problem will be due in a week from the date assigned. The problem sets will be posted on-line and will be of two types:
Simple multiple choice questions that will be autograded. You are allowed unlimited attempts at solving these problems. They are intended to help you learn by testing your concepts.
Written assignment: We will have a few longer, more open ended problems. These have to be solved on paper and turned in at the beginning of the lecture on the due date.
The score for each week will include 25 of the contribution from online assignment and 75 from the written (turned in) assignment.
Emailed assignments will not be graded. .
Weekly assignments will normally be due on a thursday.
To be flexible, we will omit two assignments with the lowest scores from consideration while computing the overall grade.
Examinations
The course will have a quiz every 4 weeks. The dates for the quizzes will be posted well in advance. Each quiz will be 30 minutes long, and will focus on the material corresponding to a set of lectures.
No alternate exams will be offered unless there is a very compelling and documented personal or medical emergency. If you need special accommodations of any nature, you are expected to inform the instructor well in advance.
The lowest quiz will be dropped for the purposes of computing the grade.
It is compulsory to attend the final exam and score at least a 25% to obtain a pass in this course.
Course Participation
Class participation is awarded based mainly on your class preparation, as judged by your general attendance, classroom behavior, interaction in class, willingness to answer questions in class and at the on-line forums, and demonstrating knowledge of weekly reading during problem solving time.
Grading
The overall grade will be based on a cumulative score computed by adding together the grades from:
The weekly assignments (with least two scores omitted),
The programming assignments (ideally, we hope to have two assignments over the semester),
The grades from the quizzes (with least grade omitted).
The final exam.
Class participation: you are expected to attend class and in class you are expected to interact with the instructor.
Overall, the contributions to the final grades will be:
Assignments Weekly (35% of the grade).
In-Class Quizzes (30% of the grade cumulatively).
Final exam (25% of the grade).
Participation (10% of the grade).
The instructor may make minor modifications to this breakup as the semester progresses.
Note: To obtain a passing grade, the student has to appear for the final exam and obtain a score of at least 25/100 or above.
The final grades will be based on the cumulative score from all these factors (out of 100).
Collaboration Policy
The collaboration policy is rather simple:
Inspiration is free: you may discuss homework assignments with anyone. You are especially encouraged to discuss solutions with your instructor and your classmates.
Plagiarism is forbidden: the assignments that you turn in should be written entirely on your own. While writing the assignment you are not allowed to consult any source other than the textbook(s) for the class, your own class notes or the lecture notes for the class. Copying/consulting from the solution of another classmate constitutes a violation of the course's collaboration policy and the honor code.
Do not search for a solution on-line: You may not actively search for a solution to the problem from the internet. This includes posting to newsgroup or asking experts at other universities.
When in doubt, ask: If you have doubts about this policy or would like to discuss specific cases, please ask the instructor.
Honor Code
We will expect strict adherence to our our honor code. Please read and understand the code thoroughly. If in doubt, ask the instructor. At the end of the day, honor code violators hurt themselves by sacrificing their integrity and risking hard-earned reputation for a few measly grade points.