A Quick Tutorial on Pollard's Rho Algorithm
Pollard's Rho Algorithm is a very interesting and quite accessible algorithm for factoring numbers. It is not the fastest algorithm by far but in practice it outperforms trial division by many orders of magnitude. It is based on very simple ideas that can be used in other contexts as well.
History
The original reference for this algorithm is a paper by John M. Pollard (who has many contributions to computational number theory).
Pollard, J. M. (1975), “A Monte Carlo method for factorization”, BIT Numerical Mathematics 15 (3): 331–334
Improvements were suggested by Richard Brent in a follow up paper that appeared in 1980
Brent, Richard P. (1980), “An Improved Monte Carlo Factorization Algorithm”, BIT 20: 176–184, doi:10.1007/BF01933190
A good reference to this algorithm is by Cormen, Leiserson and Rivest in their book. They discuss integer factorization and Pollard's rho algorithm.
Problem Setup
Let us assume that 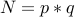 is a number to be factorized and
is a number to be factorized and  . Our goal is to find one of the factors
. Our goal is to find one of the factors 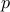 or
or 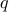 (the other can be found by dividing from
(the other can be found by dividing from  ).
).
We saw the trial division algorithm
int main (int argc, char * const argv []) { int N,i; // Read in the number N scanf("%d", &N); printf ("You entered N = %d \n", N); if (N %2 == 0) { puts ("2 is a factor"); exit(1); } for (i = 3; i < N; i+= 2){ if (N % i == 0) { printf ("%d is a factor \n", i); exit(1); } } printf("No factor found. \n"); return 1; }
Let us try an even more atrocious version that uses random numbers. Note that the code below is not perfect but it will do.
int main (int argc, char * const argv []) { int N,i; // Read in the number N scanf("%d", &N); printf ("You entered N = %d \n", N); i = 2 + rand(); // Gets a number from 0 to RAND_MAX if (N % i == 0) { printf(" I found %d \n", i); exit(1); } printf ("go fishing!\n"); }
The I am feeling lucky algorithm (no offense to google) generates a random number between  and
and 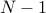 and checks if we found a factor. What are the odds of finding a factor?
and checks if we found a factor. What are the odds of finding a factor?
Very simple: we have precisely two factors to find 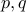 in the entire space and
in the entire space and 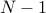 numbers. Therefore,
the probability is
numbers. Therefore,
the probability is 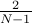 . If
. If 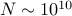 (a 10 digit number), the chances are very much not in our favor about
(a 10 digit number), the chances are very much not in our favor about 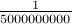 . Now the odds for winning Lotto are much better than this.
. Now the odds for winning Lotto are much better than this.
Put another way, we have to repeatedly run the I am feeling lucky algorithm approximately  times with different random numbers to find an answer. This is absolutely no better than trial division.
times with different random numbers to find an answer. This is absolutely no better than trial division.
Improving the Odds with Birthday Trick
There is a simple trick to improve the odds and it is a very useful one too. It is called the Birthday Trick. Let us illustrate this trick.
Suppose we randomly pick a number uniformly at random from  to
to 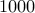 . What are the chances that we land on the number
. What are the chances that we land on the number 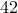 . The answer is very simple:
. The answer is very simple: 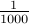 . Each number is equally probable and getting
. Each number is equally probable and getting 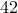 is just as likely as picking any other number, really.
is just as likely as picking any other number, really.
But suppose we modify the problem a little: we pick two random numbers 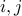 from
from  to
to 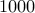 . What are the odds that
. What are the odds that  ? Note that
? Note that  need not be different. There are roughly
need not be different. There are roughly 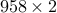 possible values of
possible values of  that ensure that
that ensure that  and the probability reduces to
and the probability reduces to 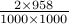 and
it works out to roughly
and
it works out to roughly 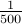 .
.
Rather than insist that we pick one number and it be exactly 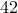 , if we are allowed to pick two and just ask that their difference be
, if we are allowed to pick two and just ask that their difference be 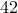 , the odds improve.
, the odds improve.
What if we pick 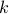 numbers
numbers  in the range
in the range ![[1,1000]](eqs/1254336469854302880-130.png) and ask whether any two numbers
and ask whether any two numbers 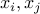 satisfy
satisfy 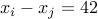 ? How do the odds relate to
? How do the odds relate to 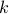 ? The calculation is not hard but let us write a simple
program to empirically estimate the odds.
? The calculation is not hard but let us write a simple
program to empirically estimate the odds.
#include <stdio.h> #include <stdlib.h> int main(int argc, int * argv){ int i,j,k,success; int nTrials = 100000, nSucc = 0,l; int * p; /* Read in the number k */ printf ("Enter k:"); scanf ("%d", &k); printf ("\n You entered k = %d \n", k); if ( k < 2){ printf (" select a k >= 2 please. \n"); return 1; } /* Allocate memory */ p = (int *) malloc(k * sizeof(int)); // nTrials = number of times to repeat the experiment. for (j = 0; j < nTrials; ++j){ success = 0; // Each experiment will generate k random variables // and check whether the difference between // any two of the generated variables is exactly 42. // The loop below folds both in. for (i = 0; i < k; ++i){ // Generate the random numbers between 1 and 1000 p[i] = 1+ (int) ( 1000.0 * (double) rand() / (double) RAND_MAX ); // Check whether a difference of 42 has been achieved already for (l = 0; l < i; ++l) if (p[l] - p[i] == 42 || p[i] - p[l] == 42 ){ success = 1; // Success: we found a diff of 42 break; } } if (success == 1){ // We track the number of successes so far. nSucc ++; } } // Probability is simply estimated by number of success/ number of trials. printf ("Est. probability is %f \n", (double) nSucc/ (double) nTrials); // Do not forget to cleanup the memory. free(p); return 1; }
You can run the code for various values of 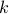 starting from
starting from 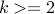 .
.
| k | Prob. Est. |
| 2 | 0.0018 |
| 3 | 0.0054 |
| 4 | 0.01123 |
| 5 | 0.018 |
| 6 | 0.0284 |
| 10 | 0.08196 |
| 15 | 0.18204 |
| 20 | 0.30648 |
| 25 | 0.4376 |
| 30 | 0.566 |
| 100 | 0.9999 |
This shows a curious property. Around 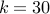 there is more than a half probability of success. We have a large set of numbers
there is more than a half probability of success. We have a large set of numbers 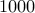 but generating about
but generating about 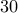 random numbers gets us a half probability of success. Around
random numbers gets us a half probability of success. Around 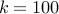 , we are virtually assured of success. This is an important observation and it is called the
birthday problem or the birthday paradox.
, we are virtually assured of success. This is an important observation and it is called the
birthday problem or the birthday paradox.
Suppose we pick a person at random and ask what is the probability that their birthday is the April 1st.
Well, the answer is 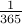 assuming that no leap years exist.
assuming that no leap years exist.
We number the days in the year from  to
to  and April 1st is roughly day number
and April 1st is roughly day number 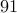 . Since each day is
equally probable as a birthday, we get to
. Since each day is
equally probable as a birthday, we get to 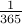 . We can play the same game as before.
. We can play the same game as before.
Let us take 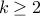 people at random and ask the probability that they have the same birthday.
A quick modification of our difference of
people at random and ask the probability that they have the same birthday.
A quick modification of our difference of 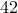 code yields the answers we want
code yields the answers we want
#include <stdio.h> #include <stdlib.h> int main(int argc, int * argv){ int i,j,k,success; int nTrials = 100000, nSucc = 0,l; int * p; printf ("Enter k:"); scanf ("%d", &k); printf ("\n You entered k = %d \n", k); p = (int *) malloc(k * sizeof(int)); // We will do 1000 reps for (j = 0; j < nTrials; ++j){ success = 0; for (i = 0; i < k; ++i){ // Generate the random numbers between 1 and 365 p[i] = 1+ (int) ( 365 * (double) rand() / (double) RAND_MAX ); // Check whether a difference of 42 has been achieved for (l = 0; l < i; ++l) if (p[l] - p[i] == 0 ){ success = 1; break; } } if (success == 1){ nSucc ++; } } printf ("Est. probability is %f \n", (double) nSucc/ (double) nTrials); return 1; }
We can see that with 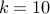 people there is a roughly
people there is a roughly 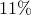 chance of having two people with the same birthday.
With
chance of having two people with the same birthday.
With 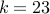 people, we have a roughly
people, we have a roughly 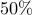 chance. Our class size is
chance. Our class size is 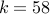 and we have roughly
and we have roughly 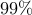 chance
of having two people having the same birthday. We get mathematical certainty
chance
of having two people having the same birthday. We get mathematical certainty 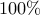 chance with
chance with 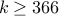 .
.
If we have  days in a year (
days in a year (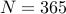 on this planet) then with
on this planet) then with 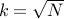 people we have a 50% chance
of having a birthday collision.
people we have a 50% chance
of having a birthday collision.
Imagine a version of star trek where the enterprise docks on a strange new planet and they are unable to find out how long a year is. Captain Kirk and Officer Spock land on the planet and walk over to the birth records. They toss coins to pick people at random and look at how many people give them even odds of birthday collision. They can back out the revolution period of the planet divided by its rotational period (i.e, number of days in the year).
This is all well and good, you say. How does this help us at all?
Applying Birthday Paradox to Factoring
Let us go back to the I am feeling lucky algorithm. We are given 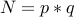 and we randomly picked a number
between
and we randomly picked a number
between  and
and  . Chances of landing on either
. Chances of landing on either 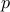 or
or 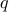 are quite small. So we have to repeat the algorithm many many times to get us to even odds.
are quite small. So we have to repeat the algorithm many many times to get us to even odds.
We can ask a different question. Instead of picking just one number, we can pick 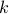 numbers for some
numbers for some 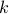 .
Let these numbers be
.
Let these numbers be 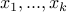 . We can now ask if
. We can now ask if 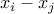 divides
divides  .
.
The difference between the former scheme and latter is exactly the difference between picking one person and asking if their birthday falls on April the 1st (a specific day) or picking 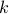 people and asking if any two
among
people and asking if any two
among 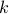 share a birthday. We can already see that for
share a birthday. We can already see that for 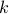 roughly around
roughly around 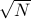 , we get even odds. So
very roughly speaking, we can improve the chances from roughly
, we get even odds. So
very roughly speaking, we can improve the chances from roughly 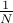 to
to 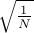 . Therefore,
for a
. Therefore,
for a 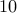 digit number, instead of doing
digit number, instead of doing  reps, we can pick
reps, we can pick 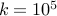 random numbers and do the
test above.
random numbers and do the
test above.
But unfortunately, this does not save us any effort. With 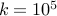 people, we still do
people, we still do  pairwise
comparisons and divisions. Bah.. there's got to be a better way :-)
pairwise
comparisons and divisions. Bah.. there's got to be a better way :-)
We can do something even better.
We can pick numbers  and instead of asking if
and instead of asking if 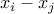 divides
divides  , we can ask if
, we can ask if
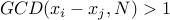 . In other words, we ask if
. In other words, we ask if 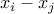 and
and  have a non-trivial factor in common.
This at once increases the number of chances for successes.
have a non-trivial factor in common.
This at once increases the number of chances for successes.
If we ask how many numbers divide  , we have just 2 :
, we have just 2 :  .
.
If we ask how many numbers have 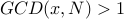 , we have quite a few now:
, we have quite a few now:

Precisely, we have 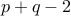 of these numbers.
of these numbers.
So a simple scheme is as follows:
Pick
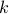 numbers
numbers 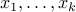 uniformly at random between
uniformly at random between 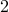 and
and 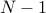 .
. Ask if
 . If yes, then
. If yes, then  is a factor of
is a factor of  (either
(either 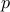 or
or 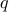 ).
).
But there is already a problem, we need to pick a number 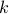 that is in the order of
that is in the order of 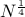 and do pairwise
comparisons. This is already too much to store in the memory. If
and do pairwise
comparisons. This is already too much to store in the memory. If 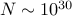 , we are storing about
, we are storing about 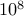 numbers in memory.
numbers in memory.
To get to Pollard's rho algorithm, we want to do things so that we just have two numbers in memory.
Pollard's Rho Algorithm
Therefore, Pollard's rho algorithm works like this. We would like to generate 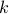 numbers
numbers  and check pairwise but we cannot. The next best thing is to generate random numbers one by one and check
two consecutive numbers. We keep doing this for a while and hopefully we are going to get lucky.
and check pairwise but we cannot. The next best thing is to generate random numbers one by one and check
two consecutive numbers. We keep doing this for a while and hopefully we are going to get lucky.
We use a function 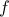 that will generate pseudo random numbers. In other words, we will keep applying
that will generate pseudo random numbers. In other words, we will keep applying 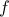 and it will generate numbers that “look and feel” random. Not every function does it but one such function that has mysterious pseudo random property is
and it will generate numbers that “look and feel” random. Not every function does it but one such function that has mysterious pseudo random property is
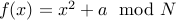 , where we generate
, where we generate  using a random number generator.
using a random number generator.
We start with  or some other number. We do
or some other number. We do 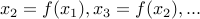 . The general rule
is
. The general rule
is 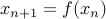 .
.
We can start off with a naive algorithm and start to fix the problems as we go.
x := 2;
while (.. exit criterion .. )
y := f(x);
p := GCD( | y - x | , N);
if ( p > 1)
return "Found factor: p";
x := y;
end
return "Failed. :-("
Let us take 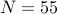 and
and  .
.
In the table below GCD refers to 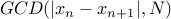 .
.
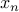 | 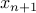 | GCD |
| 2 | 6 | 1 |
| 6 | 38 | 1 |
| 38 | 16 | 1 |
| 16 | 36 | 5 :-) |
You can see that in many cases this works. But in some cases, it goes into an infinite loop because, the function 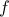 cycles. When that happens, we keep repeating the same set of value pairs
cycles. When that happens, we keep repeating the same set of value pairs 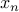 and
and 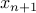 and never stop.
and never stop.
For example, we can make up a pseudo random function 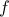 which gives us a sequence like
which gives us a sequence like
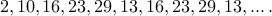
In this case, we will keep cycling and never find a factor. How do we detect that the cycling has happened?
Solution #1 is to keep all the numbers seen so far 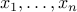 and see if
and see if 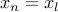 for some previous
for some previous
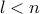 . This gets back to our memory crunch as
. This gets back to our memory crunch as 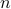 is going to be large in practice.
is going to be large in practice.
Solution #2 is a clever algorithm by Floyd. To illustrate Floyd's algorithm, suppose we are running on a long circular race track, how do we know we have completed one cycle? We could use solution #1 and remember everything we have seen so far. But a cleverer solution is to have two runners A and B with B running twice as fast as A.
They start off at the same position and when 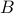 overtakes
overtakes 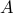 , we know that
, we know that 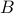 has cycled around at least once.
has cycled around at least once.
a = 2;
b = 2;
while ( b != a ){
// a runs once
a = f(a);
// b runs twice as fast.
b = f(f(b));
p = GCD( | b - a | , N);
if ( p > 1)
return "Found factor: p";
}
return "Failed. :-("
If the algorithm fails, we simply find a new function 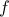 or start from a new random seed for
or start from a new random seed for  .
.
Now we have derived the full Pollard's rho algorithm with Floyd's cycle detection scheme. Hope you were able to follow this presentation.
You may find the wikipedia presentation on cycle detection quite useful. It also explains the use of Bernt's cycle finding algorithm in this context.