Tutorial on GMP
GMP stands for the Gnu MultiPrecision Library. It is a popular library that gives us the ability to operate with arbitrary precision integers, rationals and floating point numbers: the add on MPFR library is useful for arbitrary precision floating point.
The tutorial focusses on the C part of the library. There is an extension to C that is much easier to use. But starting off with the C part of the library gives us better control over what can be done and a better understanding of how the library works.
Getting Started
I will assume access to a linux machine with GMP installed. GMP can be downloaded from the gmplib.org website.
The user manual for the latest version is here
What is arbitrary precision? Why do we need it?
Computers process numbers 32 or 64 bits at a time. If you write a program in C and declare int x, the int is a 32 bit number or sometimes 64 bits. It all depends on your machine and your compiler.
You can discover all this by writing a little bit of C code as below:
#include <stdio.h> #include <assert.h> #include <limits.h> int main(){ int k,x,i; /* 1. Print the machine native <span class="builtin">int</span> size and the max/min integer */ printf ("Size of integers in this computer = %d bits \n", sizeof(int) * 8); printf ("The largest int representable is %d \n", INT_MAX); printf ("The smallest int representable is %d \n", INT_MIN); /* 2. Let us add 1 to INT_MAX */ k = INT_MAX; printf (" %d + 1 = %d \n", k,k+1); /* 3. Input a number x and print its binary representation out */ printf ("Enter x:"); scanf("%d",&x); printf ("The binary reprentation LSB --> MSB is: "); for (i=0; i < 8 * sizeof(int); ++i){ if (x %2 == 0) printf ("0"); else printf("1"); x = x >> 1; / Shift right by 1 } printf ("\n"); }
sizeof(int) gives the number of bytes for an integer. INT_MAX is macro defined in limits.h to the largest possible integer. Similarly for INT_MIN.
I compiled this on MAC and got the following output.
Size of integers in this computer = 32 bits The largest int representable is 2147483647 The smallest int representable is -2147483648 2147483647 + 1 = -2147483648 Enter x:3091 The binary reprentation LSB --> MSB is: 11001000001100000000000000000000
Notice that the computer can represent numbers in the range -2147483648 to 2137483647. Any attempt to add one to the maximum int wraps around to the minimum integer.
This is fine for most applications that need some addition. For instance, a bank has to worry if someone has 2 billion or more dollars in their account that if they deposit a single dollar, their balance will wrap around.
C also has a type long that supports 64 bit arithmetic. In fact, intel processors manufactured today have 64 bit word sizes. Moving to 64 bits roughly gives us a LONG_MAX with 20 decimal digits. But it is still a limit.
Here is a more fun demonstration of precision limits.
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
int fact(int n){
/*
Function: fact (n)
Returns: n!
*/
int i;
int p = 1;
for (i=1; i <= n ; ++i){
p = p * i;
}
return p;
}
int main(int argc, char * argv[]){
int n;
if (argc <= 1){
/* Check if user has a command line argument */
printf ("Usage: %s <number>", argv[0]);
return 2;
}
n = atoi(argv[1]); /* Extract the command line argument */
assert( n >= 0);
/* Print the factorial */
printf ("%d ! = %d \n", n, fact(n));
return 1;
}
We can compile the code above and play with it.
bash-3.2$ gcc -o fact fact.c bash-3.2$ ./fact Usage: ./fact <number> bash-3.2$ ./fact 15 15 ! = 2004310016 bash-3.2$ ./fact 16 16 ! = 2004189184 bash-3.2$ ./fact 17 17 ! = -288522240 bash-3.2$ ./fact 18 18 ! = -898433024 bash-3.2$ ./fact 19 19 ! = 109641728 bash-3.2$ ./fact 20 20 ! = -2102132736 bash-3.2$ ./fact 21 21 ! = -1195114496 bash-3.2$ ./fact 22 22 ! = -522715136 bash-3.2$ ./fact 23 23 ! = 862453760 bash-3.2$ ./fact 24 24 ! = -775946240 bash-3.2$ ./fact 25 25 ! = 2076180480 bash-3.2$ ./fact 26 26 ! = -1853882368 bash-3.2$ ./fact 27 27 ! = 1484783616 bash-3.2$ ./fact 28 28 ! = -1375731712 bash-3.2$
Why is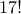 
a negative number? :-)
Arbitrary Precision Arithmetic
GMP allows us to use integers whose sizes can grow dynamically to the required precision. So by putting many words together, it can support 128, 256 or 1024 bits. There is no need for us to specify this. The library will dynamically allocate memory for accomodating extra bits of precision as and when needed.
Installing GMP on your Machine
This is the hardest part, really: (a) install the GMP thingy on your computer and (b) integrate into whatever SDK you are using to compile C or C programs.
I personally have experience with linux machines, windows machines running CYGWIN and MAC OSX with macports.
On a linux machine, the easiest way is to use a package manager apt-get, rpm or yum to install. Redhat machines use RPM whereas apt-get is popular on ubuntu machines. If you are using a basic debian linux install, then you can use dpkg.
If your system is managed by some other admin (eg., CSEL lab systems), ask your admin to install gmp. GMP will be installed globally for all users. You can find out by checking
bash-3.2$ locate libgmp.a /sw/lib/libgmp.a
On my office desktop running linux
srirams@turing:~$ locate libgmp.a /usr/lib/libgmp.a
GMP Integer Basics
Here is a simple C program that will read in a number, add 1 to it and print the result.
#include <gmp.h>
#include <stdio.h>
#include <assert.h>
int main(){
char inputStr[1024];
/*
mpz_t is the type defined for GMP integers.
It is a pointer to the internals of the GMP integer data structure
*/
mpz_t n;
int flag;
printf ("Enter your number: ");
scanf("%1023s" , inputStr); /* NOTE: never every write a call scanf ("%s", inputStr);
You are leaving a security hole in your code. */
/* 1. Initialize the number */
mpz_init(n);
mpz_set_ui(n,0);
/* 2. Parse the input string as a base 10 number */
flag = mpz_set_str(n,inputStr, 10);
assert (flag == 0); /* If flag is not 0 then the operation failed */
/* Print n */
printf ("n = ");
mpz_out_str(stdout,10,n);
printf ("\n");
/* 3. Add one to the number */
mpz_add_ui(n,n,1); /* n = n + 1 */
/* 4. Print the result */
printf (" n +1 = ");
mpz_out_str(stdout,10,n);
printf ("\n");
/* 5. Square n+1 */
mpz_mul(n,n,n); /* n = n * n */
printf (" (n +1)^2 = ");
mpz_out_str(stdout,10,n);
printf ("\n");
/* 6. Clean up the mpz_t handles or else we will leak memory */
mpz_clear(n);
}
Compiling the code (assuming GMP is installed globally in the “standard” path):
$ gcc -o mpz_simple1 mpz_simple1.c -lgmp
If GMP is not installed in the standard path, then you have to compile like this after you find out the location of gmp.h and libgmp.a. Here is what I had to do to get it to install on my laptop.
$ locate "/gmp.h" /sw/include/gmp.h $ locate "libgmp.a" /sw/lib/libgmp.a $ gcc -o mpz_simple1 -I /sw/include -L/sw/lib mpz_simple1.c -lgmp
If everything compiles fine, you will get an executable. In this case, mpz_simple1.
$ ./mpz_simple1 Enter your number: 6 n = 6 n +1 = 7 (n +1)^2 = 49
If you decide to go beserk on n, then no problem :-)
$ ./mpz_simple1 Enter your number: 1981098309851092850192851029581029581209581092581209581209581029581209581209856120856120958120958120958120958 n = 1981098309851092850192851029581029581209581092581209581209581029581209581209856120856120958120958120958120958 n +1 = 1981098309851092850192851029581029581209581092581209581209581029581209581209856120856120958120958120958120959 (n +1)^2 = 39247505132948566943624540368331641284... a really long number...
To understand the code above better you will need to consult the GMP manual on integer functions: GMP Integer Functions.
Here is a skeleton of the code.
#include <gmp.h>
/* la di da di da ... */
mpz_t n;
mpz_init(n);
/* blah blah */
mpz_set_ui(n,0);
/* blah blah */
mpz_clear(n);
mpz_t is a pointer to some complicated data structure that GMP has for storing arbitrary precision integers. We do not care about what mpz_t contains. But remember that it is a pointer. We call it a handle to the int. Examining the value of n will not be very meaningful.
mpz_init(n) calls the init function and tells it to properly initialize n.
mpz_set_ui(n,0) asks GMP to set the number n to 0.
mpz_clear(n) asks GMP to deallocate the memory that it has stored for n.
GMP Factorial Code
#include "gmp.h"
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
void fact(int n){
int i;
mpz_t p;
mpz_init_set_ui(p,1); /* p = 1 */
for (i=1; i <= n ; ++i){
mpz_mul_ui(p,p,i); /* p = p * i */
}
printf ("%d! = ", n);
mpz_out_str(stdout,10,p);
mpz_clear(p);
}
int main(int argc, char * argv[]){
int n;
if (argc <= 1){
printf ("Usage: %s <number> \n", argv[0]);
return 2;
}
n = atoi(argv[1]);
assert( n >= 0);
fact(n);
return 1;
}
The code above fixes the issues we found due to overflow in the original native int factorial function.
$ gcc -I /sw/include/ -L/sw/lib -o mpz_fact mpz_fact.c -lgmp $ ./mpz_fact Usage: ./mpz_fact <number> $ ./mpz_fact 1093 1093! = 279512617852590467904571737438372389.... and a buzillion more digits ;-) $ $ ./mpz_fact 109 109! = 1443859583202493582204882102462... goes on and on and on.. :-) $ ./mpz_fact 10 10! = 3628800 $ ./mpz_fact 15 15! = 1307674368000 $ ./mpz_fact 16 16! = 20922789888000 $ ./mpz_fact 17 17! = 355687428096000 $ ./mpz_fact 19 19! = 121645100408832000 $ ./mpz_fact 2091 2091! = 64536472071648725652592612640419881740...and a guzzillion more digits :-)
Useful GMP Integer Functions
GMP provides a lot of useful integer functions: Integer Arithmetic
You will find some number theoretic functions useful: here