Proofs — Existential statements (CSCI 2824, Spring 2015)
In this series of notes, we are going to
Provide proofs of various propositions
Ask you to fix some of our proofs.
Practice proving theorems by expressing your argument in a succinct and logically consistent form.
In this page, we briefly discuss existential statements, and their common proof strategies.
Existential Statements
We will mention existential statements. They are rarer but interesting.
Simple existential statements assert that a number with some property exists.
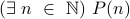 .
.
To prove an existential statement, we just give an example.
Example
Theorem There exist two prime numbers whose sum is also a prime number.
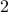 and
and 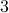 serve as examples to our theorem.
serve as examples to our theorem.
A first look at constructive Proofs
Existential statements can be proved in another way without producing an example. Typically this involves a proof by contradiction (we will study these types of proofs soon). Such proofs are called non-constructive proofs.
Theorem There exist two irrational numbers  and
and 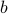 such that
such that 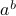 is rational.
is rational.
We will show that such numbers exist without giving you a concrete example.
Consider the number 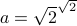 and
and  .
.
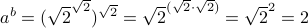
Therefore 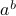 is rational. We know that
is rational. We know that 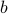 is irrational.
is irrational.
There are two cases:
 is irrational. In that case, we are done since
is irrational. In that case, we are done since 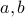 are both irrational and
are both irrational and 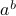 is rational.
is rational.  is rational.
is rational. In that case,
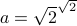 is rational.
is rational. But
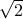 is irrational itself.
is irrational itself. So in this case, we have
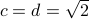 are irrational and
are irrational and 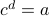 is rational by assumption.
is rational by assumption.
As a result, there must exist two numbers 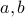 such that
such that 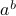 is rational while
is rational while 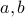 themselves are irrational.
( Our argument just has not produced any concrete example to point to. :-) )
themselves are irrational.
( Our argument just has not produced any concrete example to point to. :-) )
QED.
Needless to say we will leave non-constructive proofs to mathematicians and the debate to the philosophers for now. If you are interested, these ideas are usually covered in a philosophy of mathematics or a philosophy of science class.