Proofs — Extra material on divisibility (CSCI 2824, Spring 2015)
In this lecture we will cover:
Divisibility of numbers and modular arithmetic.
Some proofs involving divisibility.
This covers part of Chapter 2.2 of the book.
Proving Properties of Numbers
Let us start with divisibility.
An integer  is divisible by a non-zero integer
is divisible by a non-zero integer 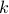 , if
, if  can
be written as
can
be written as 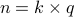 for some integers
for some integers 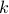 and
and 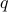 .
In logic, we write:
.
In logic, we write:
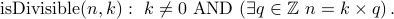
The following concepts are all equivalent:
 is divisible by
is divisible by 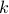
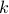 divides
divides  ,
,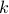 is a factor of
is a factor of  ,
, 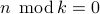 , and
, and is a multiple of
is a multiple of 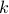 .
.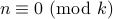 .
.
Divisibility by 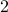 has a special name: If
has a special name: If  is divisible by
is divisible by 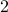 , we
call it even, and other wise we call it odd.
, we
call it even, and other wise we call it odd.
Theorem -1: If 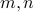 are divisible by
are divisible by  then
then 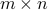 is divisible by
is divisible by 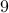 .
.
For your convenience, we split the proof step by step to make the flow of reasoning steps clear.
Let
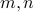 be any two given numbers such that
be any two given numbers such that 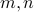 are divisible by
are divisible by  .
.Therefore, we write
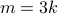 , for some integer
, for some integer 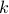 .
.And, since
 is divisible by
is divisible by  ,
, 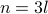 for some integers
for some integers 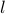 .
.We note that
 .
. Therefore
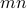 is divisible by
is divisible by 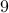 .
.
Whenever in a proof, a number can be written as 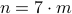 , we conclude that
, we conclude that  is divisible by
is divisible by 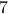 . Similarly,
if you are told that a number is divisible by
. Similarly,
if you are told that a number is divisible by 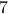 , it makes sense to
write it as
, it makes sense to
write it as 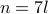 for some
for some 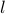 .
.
Theorem-2 If  is divisible by
is divisible by 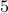 and
and 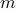 by
by  then
then 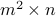 is divisible by
is divisible by  .
.
Let
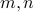 be any given numbers such that
be any given numbers such that 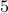 divides
divides  and
and  divides
divides 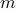 .
.Therefore, we write
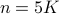 for some integer
for some integer 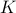 , and
, and  for some integer
for some integer 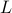 .
. The number
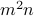 may be written as:
may be written as:
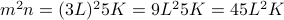 .
. Therefore
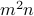 is divisible by
is divisible by  .
.
Proofs on Consecutive Numbers
Theorem-3 The product of two consecutive numbers is always even.
Let
 be any given number and
be any given number and 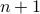 be the next consecutive numbers.
be the next consecutive numbers.We will show that
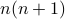 is even.
is even.We note that there are two cases based on whether
 is odd or even.
is odd or even.
-
Case-1:
 is odd. In this case, we have
is odd. In this case, we have 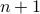 being even. Therefore
being even. Therefore 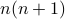 =
= 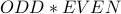 which is EVEN.
which is EVEN. Case-2:
 is even. In this case
is even. In this case 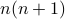 is even too.
is even too.
In either case,
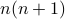 is even. QED.
is even. QED.
Proofs by Case-Splitting
A number 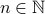 is a perfect square if
is a perfect square if 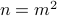 for
some
for
some 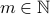 . Examples of perfect squares include
. Examples of perfect squares include
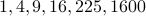 and so on.
and so on.
Theorem-4 If a perfect square is even, then it is divisible by 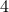 .
.
Let
 be any given perfect square that is even.
be any given perfect square that is even.Since
 is a perfect square, can be written as
is a perfect square, can be written as 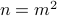 for some
for some 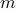 .
.We consider two cases based on whether
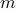 is odd or even.
is odd or even.
Case-1:
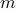 is odd.
is odd.
-
In this case, we know that
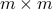 is a product of two odd numbers is odd.
is a product of two odd numbers is odd. However, this conflicts with our assumption that
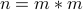 is even.
is even. Therefore, this case can never happen.
Case-2:
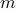 is even.
is even.
-
In this case,
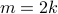 for some integer
for some integer 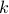 .
. 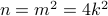 is divisible by
is divisible by 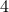 .
.
Therefore, we conclude that  must be divisible by
must be divisible by 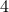 based on case 2, which is the only case that can happen.
based on case 2, which is the only case that can happen.
QED.
There are other ways of proving this theorem that we will revisit when we study proofs by contradiction.
Division theorem
We present (without proof for now) the division theorem that formalizes the notion of quotient and remainder.
Let 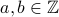 with
with 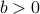 .
Then there exists a unique integer
.
Then there exists a unique integer 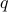 (which we call quotient)
and another unique integer
(which we call quotient)
and another unique integer  (which we call remainder)
such that
(which we call remainder)
such that
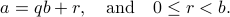
When 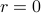 , we say that
, we say that  is a multiple of
is a multiple of 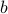 .
.
Modular Arithmetic
We have been using the “mod” operator so far in some proofs. Let us study the properties of the “mod” operator in more detail.
Let  be some integer. For a integer
be some integer. For a integer 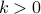 say that
say that 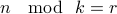 iff
iff 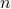 can be written as
can be written as 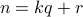 where
where
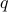 is the quotient and
is the quotient and  is the remainder when
is the remainder when  is divided by
is divided by 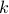 .
.
Let us look at examples.
We write 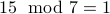 . Since
. Since 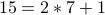 .
.
As a convention, the result of a modulo operation 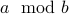 is always between
is always between 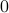 and
and 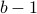 .
.
Also, we always apply over 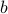 positive, but
positive, but  can be positive or
negative What is
can be positive or
negative What is  ? We write
? We write 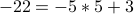 . Therefore
. Therefore
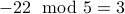 .
.
Note:
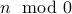 is undefined.
is undefined. We will not bother defining
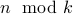 for negative
for negative 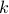 .
. We will only apply mod to integers for now. It can be defined on reals but that is not very important to us now.
Odd number: A number  is odd iff
is odd iff 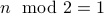 .
.
We can distribute  over
over 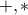 .
.
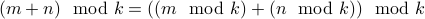
Secondly,
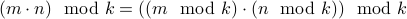
Let us prove these facts:
Theorem: Suppose number  can be written as
can be written as 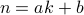 for
for 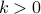 .
It follows that
.
It follows that 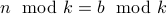 .
.
Let 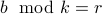 . Therefore
. Therefore 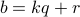 for some
for some 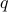 . Note that
. Note that 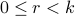 .
.
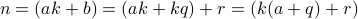
Therefore  can be written as
can be written as 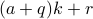 for
for 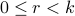 . We conclude therefore
that
. We conclude therefore
that 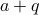 is the quotient when
is the quotient when  is divided by
is divided by 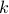 and
and  is the remainder.
Therefore,
is the remainder.
Therefore,
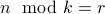
QED.
Theorem: For any integers 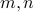 and integer
and integer 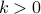 , the following statement is true:
, the following statement is true:
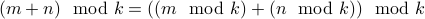
Let us assume 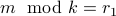 and
and 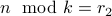 . Therefore, we may write
. Therefore, we may write 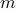 as
as
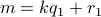 for some
for some 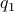 . We also write
. We also write  as
as 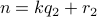 for some
for some 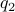 .
.
Therefore, 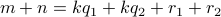 .
.
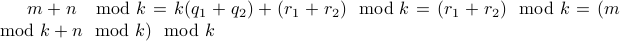
QED.
Similarly, we can prove that modulo operator distributes over multiplication.
Theorem For any integers 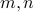 , and natural number
, and natural number 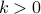 , the following statement is true:
, the following statement is true:
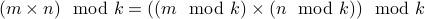
Let 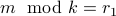 and
and 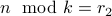 , where
, where 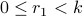 and
and 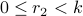 .
We can write
.
We can write
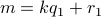 and
and 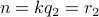 .
.
Therefore, using the distributivity of modulo operator over addition (proved in the previous theorem),
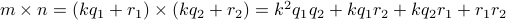
Therefore,
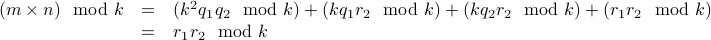
This shows that
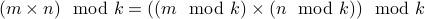
(QED)
Computing modulo
Let us try some interesting problems involving modulo arithmetic.
Example 1
For instance, let us try and compute  for various values of
for various values of  .
.
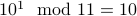
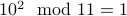
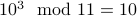
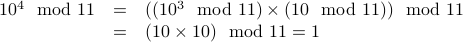 .
.
As you can see the pattern that emerges is
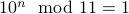 if
if  is even.
is even.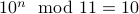 if
if  is odd.
is odd.
Example 2
We know 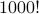 is a really large number. The question is very simple. Suppose we wrote
is a really large number. The question is very simple. Suppose we wrote 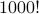 in hexadecimal, what would the last digit be?
in hexadecimal, what would the last digit be?
In general, the last digit of a number  in hexadecimal is simply computed by finding out
in hexadecimal is simply computed by finding out 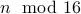 . So what is
. So what is  ?
?
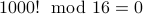 , because
, because 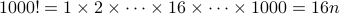 for some
for some 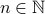 .
.
Example 3
Find the smallest natural number that leaves a remainder of 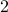 when divided by
when divided by  and a remainder of
and a remainder of 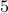 when divided by
when divided by 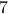 .
.
Let our mystery number be  . We require
. We require 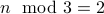 . Therefore,
. Therefore, 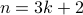 for some
for some 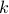 .
.
Now consider 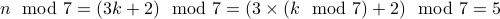 .
.
Therefore, we note that 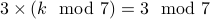 or in other words
or in other words 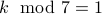 and
and 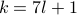 for some
for some 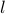 .
.
Let us choose 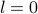 to yield
to yield 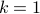 and therefore
and therefore 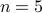 .
.
The smallest number is indeed 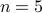 .
.
We will examine more problems of this sort when we look at the Chinese remainder theorem.