Predicates: quantifiers and implication (CSCI 2824 Spring 2015)
Today's lecture:
Quantifiers, Truth of Quantified Formulas and Negation of Quantified Formulas (Section 1.4 of the book).
Implication (Section 1.5 of the book)
Quantifiers
We have already seen two types of quantifiers in the previous lecture:
The
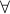 (for-all or universal ) quantifier, and
(for-all or universal ) quantifier, and The
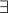 (exists or existential) quantifier.
(exists or existential) quantifier.
Truth and Quantifiers
The rule for determining the truth of a quantified statement is really simple.
Statement is of the form
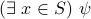 :
: Present a value
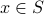 . We will plugin this value for
. We will plugin this value for 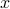 and tackle the remainder of
and tackle the remainder of 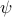 .
. If
![psi[x]](eqs/8286014233657869661-130.png) is true, then
is true, then 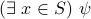 is also true.
is also true. On the other hand, if all your choices for
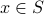 do not make
do not make ![psi[x]](eqs/8286014233657869661-130.png) true, then the formula
true, then the formula 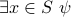 is false.
is false.
/* Checking (Exists x IN S) P */ for each x IN set S, { result := CHECK P[x]; if ( result is TRUE) then return TRUE; } /* We have gone through all values in S and they all do not satisfy P */ return FALSE;
Statement is of the form
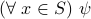 :
: Go through each and every value of
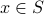 and verify that
and verify that ![psi[x]](eqs/8286014233657869661-130.png) is true.
is true. If for some value
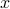 ,
, ![psi[x]](eqs/8286014233657869661-130.png) is false, then the original formula
is false, then the original formula 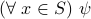 is false.
is false. Otherwise, if we have successfully verified all values, then
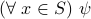 is true.
is true.
/* Checking (Forall x IN S) P */ for each x IN set S, { result := CHECK P[x]; if ( result is FALSE) then return FALSE; } /* We have gone through all values in S and all satisfy P */ return TRUE;
Caution! These two pseudocodes are only meant to illustrate the idea
of checking  - and
- and  - formulae. In practice we would
try our best avoiding using pseudocodes like these for checking,
because (1) it may be that the set
- formulae. In practice we would
try our best avoiding using pseudocodes like these for checking,
because (1) it may be that the set 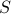 has infinitely many elements
(e.g. when
has infinitely many elements
(e.g. when  ) and (2) even if
) and (2) even if 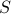 has only finitely
many element, the checking by going through everything in
has only finitely
many element, the checking by going through everything in 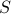 can still be very expensive!
can still be very expensive!
Formulas with Multiple Quantifiers
Formulas with multiple quantifiers can be often tricky and the order of quantification matters .
Let 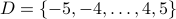 be a fixed set.
be a fixed set.
We ask whether the following formula is true:
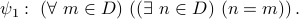
Let us run our checking algorithm. The outermost quantifier is a forall. Therefore, we plugin each value of
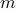 and check the inner formula:
and check the inner formula:
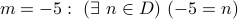 . Is this TRUE?
. Is this TRUE? 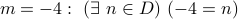 . Is this TRUE?
. Is this TRUE? 
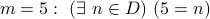 . Is this TRUE?
. Is this TRUE?
Has the inner formula 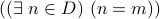 been verified for all
been verified for all 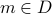 ?
?
Now let us try this formula:
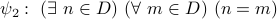
This is the same formula but with the quantifiers reversed. Does it mean the same as 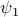 ?
Perhaps, if you paraphrase these formulae in plain language, the difference should be clear.
?
Perhaps, if you paraphrase these formulae in plain language, the difference should be clear.
Once again, we run our checking algorithm. The outermost quantifier is an 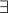 .
.
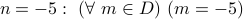 , Is this TRUE?
, Is this TRUE? 
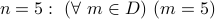 , Is this TRUE?
, Is this TRUE?
Is there indeed a value of  that makes the formula
that makes the formula 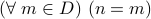 true?
true?
Negating Formulas
Let us start by negating formulas without quantifiers.
Example
What is the negation of (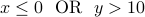 )?
)?
Answer: We start by writing 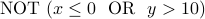 . The idea is to get rid of the
. The idea is to get rid of the 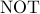 sign as much as we can.
First apply De Morgan's law:
sign as much as we can.
First apply De Morgan's law:
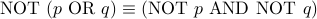
Therefore, we get
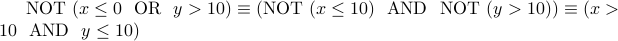
The answer is therefore 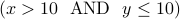 .
.
Note the following table of negations for arithmetic predicates:
| Predicate | Negation |
 |  |
 |  |
 | 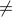
|
Negation with Quantifiers
Now we consider negation with quantifier. Proposition 1 in Page 45 of the book is the key rule here.
Negation of
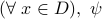 is given by
is given by 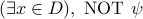 .
. Negation of
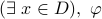 is given by
is given by 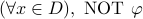 .
.
Let us try some examples.
Example
Negate the formula: 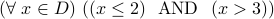 .
.
Let us do it step by step:

Is the negation true for the set 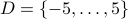 ?
?
Yes, there is indeed 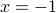 that satisifies the formula
that satisifies the formula 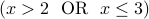 .
.
Now let us try a formula with existential quantifier: 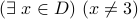 .
.
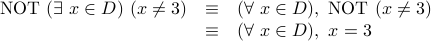
Implications
Implications are a very important concept that needs to be understood thoroughly to move forward in this course. What is an implication? Simply answer is any if.. then.. statement.
If I were a rich person then I would stop selling gadgets.
If
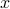 is a prime number greater than
is a prime number greater than 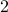 then
then 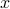 is odd.
is odd. If a real number
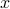 satisfies
satisfies 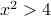 then
then 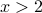 .
.
We write implications as
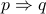
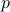 is called the premise, hypothesis or the antecedent of the implication.
is called the premise, hypothesis or the antecedent of the implication.
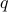 is called the conclusion.
is called the conclusion.
Example
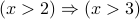 .
. 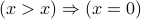 .
.
Practice Problem 1 in page 54 talks about writing down statements as implications.
Example
If a triangle has three sides then it has three equal angles.
We recast it as: for all triangles 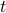 , if
, if 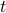 has three equal sides then
has three equal sides then 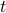 has three angles.
has three angles.
Example
If an integer is its own square then it is either 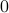 or
or  .
.
Recast it as: For all integers  , If
, If 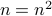 then
then 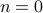 or
or 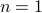 .
.
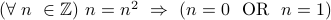
Logic of Implications
Truth Table for Implication: We noted earlier that 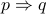 was a place holder for
was a place holder for 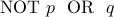 . But that barely begins
to address the entire story!
. But that barely begins
to address the entire story!
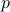 | 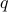 | 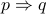 |
| T | T | T |
| T | F | F |
| F | T | T |
| F | F | T |
Note: An implication 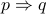 is false (or fails to hold true) only in one scenario:
is false (or fails to hold true) only in one scenario: 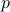 , the hypothesis is true but
, the hypothesis is true but 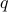 the conclusion is false.
the conclusion is false.
Example
The law says: If you are drinking alcoholic beverages, then you must be over 21 years of age.
Let us analyze the various scenarios:
| Drinking alc. bev. | Over 21 Years | Breaking Law? |
| T | T | F |
| F | T | F |
| F | F | F |
| T | F | T |
In other words, the implication is true no matter what if 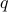 (over
(over 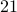 years of age?) is true OR
years of age?) is true OR
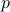 (drinking alcoholic beverates) is false.
(drinking alcoholic beverates) is false.
Example
Consider the statement: For every integer  , if
, if  is odd then
is odd then 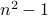 is divisible by
is divisible by 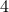 .
Is it true?
.
Is it true?
The statement is of the form 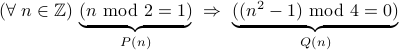 .
.
 | 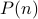 | 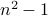 | 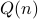 | 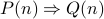 ? ? |
| 3 | T | 8 | T | Yes |
| 6 | F | 35 | F | Yes |
| 0-5 | T | 24 | T | Yes |
As you try a lot of choices, you see that it is NEVER the case where 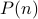 is true and
is true and 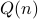 is false.
Of course, there are infinitely many cases to try so this will never convince us of the truth of the
statement, since we will never have checked all
is false.
Of course, there are infinitely many cases to try so this will never convince us of the truth of the
statement, since we will never have checked all  this way.
this way.