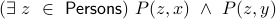Predicates (CSCI 2824 Spring 2015)
In this lecture, we will cover the following topics:
Propositional Logic: Truth tables, logical equivalence, tautologies and fallacies.
Predicates and Quantifiers (Section 1.4 of the book).
Predicates
In the previous lecture, we looked at propositions. Propositions are statements for which we can give “true” or “false” valuation. We will now generalize propositions to predicates.
Predicates should be familiar from english grammar.
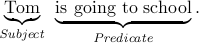
Thus, the predicate can be informally expressed as: X is going to school, where X is a variable that can stand for a person.
If we fill in values for X, such as Tom, Susan, My Fish and so on, we obtain propositions that can be given true or false valuations.
A predicate 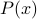 is a statement with a variable
is a statement with a variable  such that whenever
such that whenever  is substituted by a value, then it results
in a proposition that can be given true or false valuation.
is substituted by a value, then it results
in a proposition that can be given true or false valuation.
Example-1(a):
Let 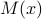 stand for the statement: __<x>__ is mortal.
stand for the statement: __<x>__ is mortal.
Q: What is 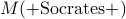 ?
?
A: The proposition Socrates is mortal.
Example-1(b):
We can use predicates in propositional formulas.
Socrates is mortal AND he NOT is the son of Zeus.
This can expressed as
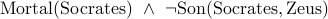 ,
,
where the predicate
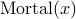 stand for the statement: __<x>__ is mortal,
and the predicate
stand for the statement: __<x>__ is mortal,
and the predicate
 stand for the statement: __<x>__ is the son of __<y>__.
stand for the statement: __<x>__ is the son of __<y>__.
Example-2:
Predicates can be arithmetic in nature. Here are some predicates over numbers:
 : Number
: Number  is less than
is less than 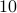 .
.  : Number
: Number  is prime.
is prime. 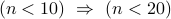 : If number
: If number  is less than
is less than 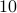 then it is less than
then it is less than  .
.
Note that we can plug in various numbers and find out if the resulting statement is true of false.
Try all statements above with
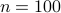 . Which ones are true?
. Which ones are true? What about with
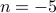 ?
?
Example-3:
Predicates can involve multiple variables.
Let 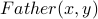 stand for the statement: __<x>__ is the father of __<y>__ .
stand for the statement: __<x>__ is the father of __<y>__ .
Q: Using the predicate above, how do we express Darth is the father of Luke?
A: 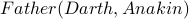 .
.
And the same applies to predicates over numbers:
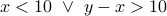 .
. 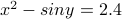
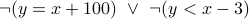 .
.
Example-4:
We can now bring in all the propositional connectives and combine them with predicates.
Q: How do we say that
( Darth is the father of Luke OR Anakin is the father of Luke) AND (Luke is NOT the father of Darth)
using the Father predicate from the previous example?
A: 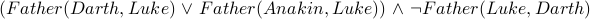 .
.
Example-5:
Let 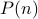 be a predicate over numbers
be a predicate over numbers  that stands for
that stands for  is prime.
is prime.
Which of the following formulae are true over numbers?
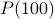
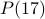
 .
.  .
.
Answers:
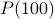 is false.
is false. 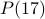 is true.
is true.  is false.
is false.  is true.
is true.
Redo the example with the following interpretation of 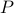 :
:  .
.
An application: Predicate logic forms the root of Prolog, which is used in artificial intelligence.
Predicates and Sets
We can use predicates to select elements from a set.
Let us fix a set 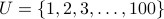 .
.
Select elements from
 that are even:
that are even: Define
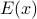 to be the predicate:
to be the predicate:  is even. We can instead write
is even. We can instead write 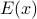 out as
out as 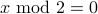 .
.We then write the set as:
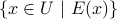 .
.Alternative notation:
 .
.Select elements from
 that are greater than
that are greater than 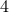 and are divisible by 13:
and are divisible by 13: 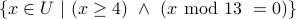 .
.
Select the empty set.
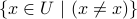 .
.
Select the entire set
 :
: 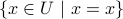 .
.
Application: SQL for database management
Structured Query Language (SQL) is a data definition and manipulation language, based on relational calculus. In plain terms, SQL allows us to query (i.e., retrieve) data that satisfies certain criteria, which would be specified using predicates.
Here is what a query looks like (syntax may be a little off), given e.g. a database db that stores a list of people and their ages.
SELECT (name, age) FROM db WHERE ( name[1]=="z" && age < 20)
This syntax uses the predicate name1==“z” && age < 20 (where name and age are the variables) and returns from the database db a list of people whose names start with “z” and who are less than 20 years old.
Negation of Predicates and Formulas
The negation of predicate 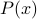 is written as
is written as 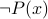 . However, this can be simplified further
by applying DeMorgan's Laws.
. However, this can be simplified further
by applying DeMorgan's Laws.
Eg., Consider the predicate  . It is cumbersome to write
. It is cumbersome to write 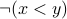 everywhere.
Instead, we write
everywhere.
Instead, we write  .
.
In other words, we say that the predicate  represents the negation of
represents the negation of  .
.
Starting from predicates, we can extend negations to formulae.
What is the negation of:
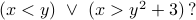
Answer:
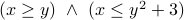
Note how the  changes to a
changes to a  while negation.
while negation.
Rules for negation:
| Formula Type | Negation |
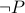 | 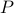 |
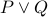 | 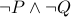 |
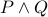 |  |
Example
Write down the negation of the following formulae:
Q1: 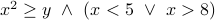 .
.
A:  .
.
Q2:  .
.
A: 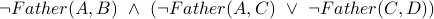 .
.
Quantifiers
The power of predicates arise from our ability to quantify. Let us illustrate quantification with an example.
How do we express the statement: For all natural numbers  ,
,  is divisible by
is divisible by 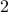 OR
OR 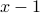 is divisible by
is divisible by 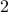 ?
?
If we forget the for all in the first place, we can write
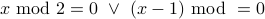
This is a formula involving a predicate that allows us to plug-in values for  . But the original
statement was meant to hold for all possible values of
. But the original
statement was meant to hold for all possible values of  .
.
We use the universal or forall quantifier to say:
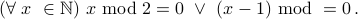
The
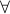 symbol is an inverted A and stands for for all or for each.
symbol is an inverted A and stands for for all or for each. The notation
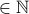 stands for belongs to the set
stands for belongs to the set 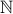 .
. The set
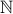 is commonly used to denote the set of natural numbers. Other commonly used notations include
is commonly used to denote the set of natural numbers. Other commonly used notations include 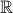 for reals,
for reals, 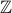 for integers and
for integers and 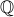 for rational numbers.
for rational numbers.
The other quantifier used is the existential or the exists quantifier. As an example, we wish to say:
There is a number  that is even and prime.
that is even and prime.
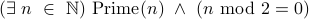
The symbol  stands for exists. Notice that it is an inverted
stands for exists. Notice that it is an inverted  .
.
Quantified Formula
Whenever there is a quantifier in front of a formula, it is called a quantified formula.
As an example consider the formula:
![psi[y]: (forall x in mathbb{R}) x leq 5 Rightarrow x - y leq 5](eqs/5609959811543716207-130.png)
In this formula the variable  is called a bound or a quantified variable.
The variable y is called a free variable.
is called a bound or a quantified variable.
The variable y is called a free variable.
We usually write formulas as ![psi[y]](eqs/8286014233656869534-130.png) to denote that
to denote that 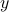 is a free variable in the formula.
is a free variable in the formula.
For example, which of the following are true for the formula above:
 ?
? 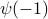 ?
?
Formulas can have multiple quantifiers in front of them:
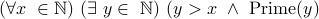
Q Paraphrase this formula in plain english.
A For every number  there exists a number
there exists a number 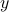 such that
such that  and
and 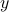 is prime.
is prime.
Q Express this sentence in Logic: “ Forall persons x,y,z, If (x is the parent of y) and ( y is the parent of z) then (x is the grandparent of z) ”. Use predicates “P(x,y)” for parent and “GP(x,y)”, grand parent.

Q Define the formula 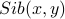 to express that
to express that  is a sibling of
is a sibling of 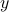 using the parent relation, where two persons are siblings if they have a parent in common.
using the parent relation, where two persons are siblings if they have a parent in common.
A: