Propositional logic and truth table (CSCI 2824 Spring 2015)
In this lecture, we will cover the following concepts:
Propositional Logic, Connectives and Truth Tables.
The truth table to analyze situations.
Equivalence of Formulae, Tautologies and Fallacies.
This lecture corresponds to section 1.3 in Ensley and Crawley's book.
Logic
In a very crude sense, logic is the assembly language of mathematics (or philosophy). Logic can be defined as the study of reasoning itself or the study of techniques for drawing valid conclusions from premises. Understanding Logic is very important to computing at many levels. For instance, propositional Logic and propositional connectives such as AND, OR and NOT form the basic building block of digital circuits from which we build modern computers. Logic is also key to areas of CS such as automata theory, programming language semantics and artificial intelligence.
Propositional Logic
What are propositions? Propositions are simply declarative statements that are either true or false, but not both.
Examples of propositions:
“Socrates is mortal”.
“Jenny went to lunch with Craig”.
“1+1=2”.
“I am telling the truth”.
“The quick brown fox jumped over the lazy brown dog”.
“If 2+2=5, then I am the richest man on earth”.
While studying propositional logic, we do not really care about what the proposition itself “means” just that it is either true or it is false.
Therefore, we simply use propositional variables (also called Boolean variables) to represent propositions. Why this? Just makes it nice and algebra like. Proposition variables can take on boolean values, i.e., T (true) or F (false).
We use letters like  and so on to represent proposition variables.
and so on to represent proposition variables.
Propositional Logic Formulae
Formulae in propositional logic are defined as follows:
Any propositional variable is a formula.
Conjunction: If
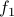 and
and 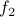 are formulas, then
are formulas, then 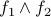 (read as
(read as 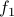 AND
AND 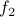 ) is a formula.
) is a formula. Disjunction: If
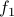 and
and 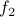 are formulas, then
are formulas, then 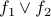 (read as
(read as 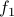 OR
OR 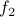 ) is a formula.
) is a formula. Negation: If
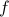 is a formula then
is a formula then 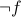 (read as NOT
(read as NOT 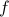 ) is a formula.
) is a formula.
Caution on “OR” operator
When we say ‘‘Either  OR
OR  is true’’, we mean that
at least one of the two propositions
is true’’, we mean that
at least one of the two propositions  ,
,  is true.
It could be that both of
is true.
It could be that both of  and
and  are true.
(See the definition in the textbook.)
are true.
(See the definition in the textbook.)
This is different from the exclusive OR (written as XOR or
 ). For any propositions
). For any propositions  and
and  ,
,
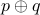 means “either
means “either  or
or  , but not both”.
, but not both”.
Let us try some examples. Read the following propositional formulae aloud:

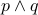
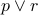
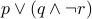
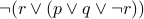 .
.
Example
Consider the following two propositions:
 : It is rainy today.
: It is rainy today. : It is sunny today.
: It is sunny today.
Then:
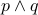 | It is rainy and sunny today. |
 | It is rainy or sunny today. |
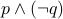 | It is rainy and not sunny today. |
Truth table
We evaluate propositional formulae using truth tables. For any given proposition formula depending on several propositional variables, we can draw a truth table considering all possible combinations of boolean values that the variables can take, and in the table we evaluate the resulting boolean value of the proposition formula for each combination of boolean values.
Truth Table for AND
 |  | 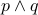 |
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
Each row represents some kind of a situation. For example, the top most row represents the
situation when propositions  and
and  are both ’'true’’. Then we conclude that the
formula
are both ’'true’’. Then we conclude that the
formula 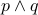 in this situation is also ’'true’’.
in this situation is also ’'true’’.
Logicians call these situations models. In this case, a Logician would
say that the truth assignment 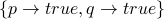 is a model
of the formula
is a model
of the formula 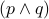 . In other words, if you imagine
a situation wherein the proposition
. In other words, if you imagine
a situation wherein the proposition  is true and the proposition
is true and the proposition  is true then
in that situation formula
is true then
in that situation formula 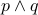 is true.
is true.
To avoid confusion let us use the term “situations” and “models”. We will formalize models later for first-order (predicate) logic.
Truth Table for OR
 |  | 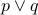 |
| T | T | T |
| T | F | T |
| F | T | T |
| F | F | F |
Can you write down all the models of  (read
(read  OR
OR  )?
)?
Does this correspond to your conception of  (the logical connective OR)?
(the logical connective OR)?
Truth Table for NOT
 | 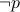 |
| T | F |
| F | T |
Truth Table for Compound Formulae
XOR is an important derived connective that is defined in terms of
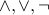 . It has the interpretation of “either-or”: i.e, either p or q, but not both.
. It has the interpretation of “either-or”: i.e, either p or q, but not both.
 XOR
XOR  is the formula
is the formula 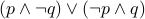 .
.
Its truth table can be written as below:
 |  | 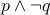 | 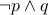 |  XOR XOR  |
| T | F | T | F | T |
| T | T | F | F | F |
| F | T | F | T | T |
| F | F | F | F | F |
We will go through few more examples of truth tables in the book.
Other examples of derived connectives are:
Implication
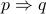 is defined as
is defined as 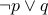 (we will study this in detail next week).
(we will study this in detail next week). Equivalence
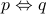 is defined as
is defined as 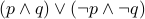 .
. Nand (a.k.a not of and)
 is defined as
is defined as 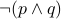 .
. NOR (a.k.a not of or)
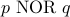 is defined as
is defined as 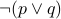
XOR (exclusive or)
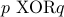 is defined as
is defined as
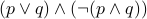 .
.
Let us write the truth table for the 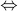 connective (equivalence connective):
connective (equivalence connective):
 |  | 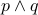 | 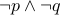 | 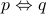 |
| T | F | F | F | F |
| T | T | T | F | T |
| F | T | F | F | F |
| F | F | F | T | T |
Tautology, Fallacies and Equivalence
Tautology
A formula is a tautology if and only if it is true no matter what value one gives to the propositions involved in the formula.
Example is 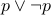 .
.
 | 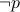 | 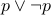 |
| T | F | T |
| F | T | T |
No matter what you value one gives  , the formula
, the formula 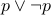 is always true.
is always true.
Other examples of tautology are
 (De Morgan's Law).
(De Morgan's Law). 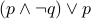 (also written as
(also written as 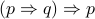 ).
). 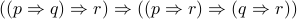 (do not even try expanding this :-)
(do not even try expanding this :-)
Fallacies
Fallacies are the opposite of tautologies. These are formulae that are false no matter what the truth values of the propositions in them.
Example: 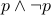 .
.
 | 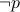 | 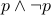 |
| T | F | F |
| F | T | F |
If we take a tautology and negate it then it becomes a fallacy.
Therefore 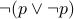 is a fallacy.
is a fallacy.
Logical Equivalence
Two formulae are logically equivalent if and only if they have the same truth value in each row
of the (joint) truth table.
When two propositional formulae  and
and  are logically equivalent,
we use the notation
are logically equivalent,
we use the notation  or
or 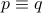 .
.
Example:
The formulae 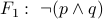 and
and 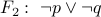 are logically equivalent.
To see why let us write their truth tables (we tack them together for convenience).
are logically equivalent.
To see why let us write their truth tables (we tack them together for convenience).
 |  | 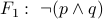 | 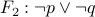 |
| T | T | F | F |
| F | T | T | T |
| T | F | T | T |
| F | F | T | T |
Notice that for all the truth table rows, 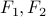 coincide.
coincide.
Examples of equivalent formulae include
 and
and 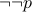 .
. 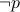 and
and 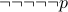 .
. 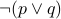 and
and 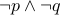 (De-Morgan's law).
(De-Morgan's law).
Technically, you need not assume that the formulae have the same set of propositions. For example, 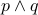 and
and
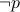 are not logically equivalent. However,
are not logically equivalent. However, 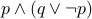 and
and  are logically equivalent.
are logically equivalent.
Similarly, 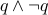 and
and 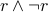 are logically equivalent since they are both fallacies.
are logically equivalent since they are both fallacies.
Example: De Morgan's laws
The De Morgan's laws are good examples of logically equivalent
formulae: for any two proposition formulae  and
and  ,
,
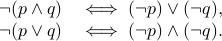
Again, the equivalence can be provde using truth tables.
Theorem:
Statement of Theorem:
Whenever two formulae 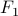 and
and 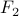 are equivalent then
are equivalent then  is a tautology.
is a tautology.
Proof: Consider the truth table for the formula  generated from a truth table
that has a column for
generated from a truth table
that has a column for 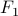 and a column for
and a column for 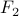 (as shown below).
(as shown below).
 | 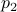 |  | 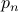 | 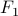 | 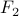 |  |
| T | T |  | F | F | F | T |
 |  | 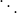 |  |  |  |  |
| F | F |  | T | T | T | T |
Note that for  column to have a false entry at some row,
column to have a false entry at some row, 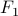 and
and 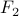 must have different
values at that row. But since
must have different
values at that row. But since 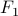 is logically equivalent to
is logically equivalent to 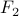 , they always have the same value at each row.
, they always have the same value at each row.
As a result, the  column must be all true, for all the rows in the truth table. Therefore
it is a tautology.
column must be all true, for all the rows in the truth table. Therefore
it is a tautology.