Basic graph theory: trees (CSCI 2824, Spring 2015)
In this lecture, we will study trees:
Basic Definition
Properties of trees with some proofs.
Trees
You have most probably studied rooted trees and binary search trees as a data-structure for organizing lists of numbers and efficiently performing insertions and deletions. However a tree is a useful structure in many other parts of CS:
Game trees in AI (how can we make computers play games like chess, go,…).
Decision trees in ML.
Spanning trees in network routing.
Parse trees for compilers.
The list goes on and on
Let us start with the simplest kind of trees: unrooted and undirected trees.
A (unrooted) tree 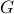 is an undirected graph
is an undirected graph 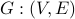 such that
such that
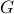 is fully connected (the entire graph is a maximally connected component),
is fully connected (the entire graph is a maximally connected component), 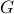 is acyclic (there are no cycles in
is acyclic (there are no cycles in  ).
).
A rooted tree  is a fully connected, acyclic graph with a special
node
is a fully connected, acyclic graph with a special
node  that is called the root of the tree. You may have
studied rooted trees in your data structures class. With a root, it is
possible to define a parent and children for each node. But
without a root, we will regard the tree simply as a connected, acyclic
graph.
that is called the root of the tree. You may have
studied rooted trees in your data structures class. With a root, it is
possible to define a parent and children for each node. But
without a root, we will regard the tree simply as a connected, acyclic
graph.
Examples
Here are some examples of unrooted trees:
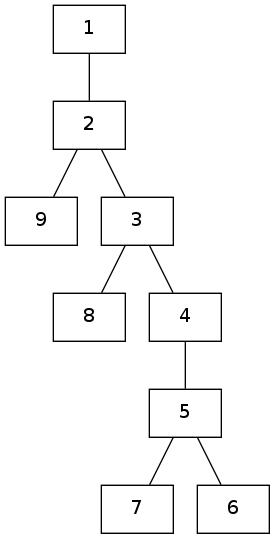 |
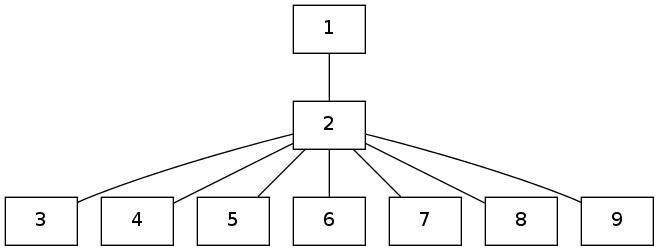 |
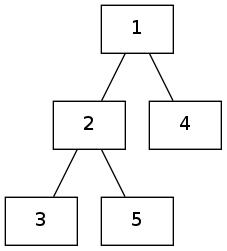 |
Non-Examples
The following graph is not a tree. It has a cycle:
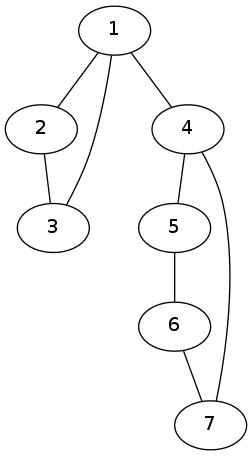 |
Here is another example that has more than one maximal connected components and is not a tree:
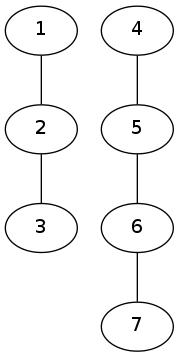 |
Properties of Trees
Leaves of a Tree
A leaf of an unrooted tree is a node that has a degree  .
Let us write down the leaves of the following tree examples:
.
Let us write down the leaves of the following tree examples:
 |
Leaves are 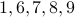 .
.
 |
Leaves are 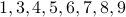 .
.
 |
Leaves are 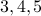 .
.
Claim Every tree has a leaf.
If the tree just has one node, then it is trivially a leaf. If the tree has two nodes connected by an edge, both nodes are leaves. Let us focus on trees with three or more nodes.
Let us assume that a tree 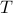 that does not have a leaf exists.
Therefore for every node
that does not have a leaf exists.
Therefore for every node  in this tree
in this tree  .
We are going to show that
.
We are going to show that 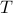 has a cycle, yielding a contradiction
with the assumption that it is a tree.
has a cycle, yielding a contradiction
with the assumption that it is a tree.
Start from any node  in the tree and do a walk as follows:
in the tree and do a walk as follows:
Take any edge out for
 to reach
to reach 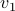 .
. For any node
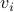 , take an edge other than the
, take an edge other than the 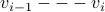 that we took to enter
that we took to enter 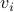 . Since
. Since 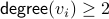 , such a vertex is always available.
, such a vertex is always available.
Note that the walk above can be continued for arbitrarily many steps. However, since number of vertices is finite, the walk repeats a vertex. Let for some 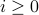 ,
,
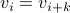 . We can now conclude the existence of a cycle with
. We can now conclude the existence of a cycle with 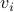 in it. Therefore
in it. Therefore 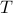 is not a tree, yielding a contradiction.
is not a tree, yielding a contradiction.
Thus, we have concluded that every tree has a leaf.
Number of Edges
Claim A tree with  nodes has
nodes has 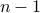 edges.
edges.
Proof is by weak induction on the number of nodes  .
.
Base Case: Take any tree with  node. There is just one such tree
and it has
node. There is just one such tree
and it has 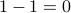 edges.
edges.
Inductive Hypothesis: Let us assume that all trees with  nodes have
nodes have 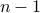 edges. We will show that all trees with
edges. We will show that all trees with 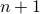 nodes have
nodes have  edges.
edges.
Take some tree  with
with 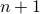 nodes. It must have a leaf
nodes. It must have a leaf  . Removing the leaf gives us a tree with
. Removing the leaf gives us a tree with  nodes that must have
nodes that must have 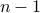 edges in it.
The leaf itself was connected to the rest of the tree by one edge. Therefore
edges in it.
The leaf itself was connected to the rest of the tree by one edge. Therefore  has
has  edges.
edges.
Number of Leaves
Claim Any tree has at least two leaves.
We will prove this in class by the following argument. We already know that any tree has at least one leaf.
Let us assume that there is a tree with 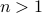 nodes and exactly one leaf
nodes and exactly one leaf  .
.
Therefore all nodes other than
 have degree
have degree  .
. Sum of degrees of all nodes
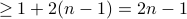 .
. However, we know that sum of degrees of all nodes = 2 * number of edges.
number of edges
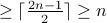 .
. However a tree has precisely
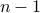 edges.
edges. This leads to a contradiction.
Paths in Trees
Claim Let 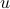 and
and  be two nodes in a tree. There is precisely one path from
be two nodes in a tree. There is precisely one path from 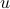 to
to  in the tree.
in the tree.
Argument in class Since the tree is connected component itself, there has to be at least one path from 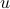 to
to  .
.
We will argue that having two distinct paths will necessarily imply that the tree has a cycle which will lead to a contradiction.