Random variables, expectation and variance
Topic covered:
random variables
expectation
variance
(Section 6.4 of the book)
Random variables
In an (random) experiment, where we have finitely many possible outcomes, often times it is natural to assign a value to each outcome.
Example 1
When tossing a die, naturally we can get a numerical outcome
from 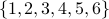 .
.
Example 2
In the case of flipping a coin, we can assign numerical values
for the head and the tail. For instance, we can define a
function 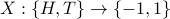 :
:
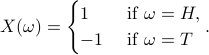
Let's imagine I have a bet with a friend on flipping a coin:
my friend would give me $1 if it is a head, and
I would give my friend $1 if it is a tail. So the amount of money I win from flipping a coin is either 1 or -1, precisely described by the function
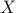 .
.
Now we can talk about what a random variable is.
In an experiment where the sample space 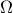 is finite
(i.e.,
is finite
(i.e., 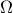 is the set of all and finitely many possible
outputs),
a random variable is a function
is the set of all and finitely many possible
outputs),
a random variable is a function  ,
where
,
where 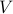 is a subset of
is a subset of 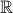 .
.
In mathematics, random variables are simply functions (when an experiment has only finitely many outcomes). In practice, we can think of random variables as measurements associating each possible outcome in an experiment with a numerical value.
We are being very careful here avoiding situations where there are infinitely many possible output. In particular, we are avoiding the likes of normal distribution and Poisson distribution, which are often encountered in real life. To fully understand the mathematics behind continuous probability distribution, one would need some basic notion of measure theory.
Expected value
Since we focus only on experiments with finitely many possible outcome, we can assume that every random variable can take on only finitely many possible values.
Suppose we have a random variable 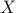 , whose output values
lie in the finite set
, whose output values
lie in the finite set 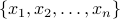 . The
expected value of
. The
expected value of 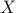 is defined as:
is defined as:
![mathbb{E}[X] triangleq x_1mathrm{Prob}(X=x_1) + x_2 mathrm{Prob}(X=x_2) + cdots + x_nmathrm{Prob}(X=x_n).](eqs/7530848817620200962-130.png)
The expected value of a random variable is simply the average value of the random variable we would get from a random experiment.
Example 3
When we throw a die, we can get one of the six possible values
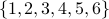 . What is the expected value of the outcome?
. What is the expected value of the outcome?
Each number can be obtained with equal probability 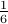 .
Hence the expected value of the outcome is
.
Hence the expected value of the outcome is
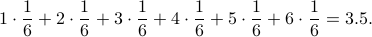
Example 4
Suppose I have a loaded coin, where
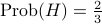 , and
, and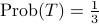 .
.
I enter a bet with a friend (as in Example 2):
I would flip my loaded coin;
if it is a head, my friend gives me $1;
if it is a tail, I give my friend $1.
What is the expected value of my gain on flipping the coin one time only?
I would get 1 dollar (by getting a
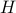 ) with probability
) with probability 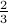 ,
and
,
and I would get -1 dollar (by getting a
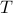 ) with probability
) with probability 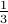 ,
,so on average, I gain
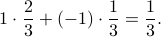
Example 5
Following up on Example 4: suppose now that we flip the coin twice. What is the expected value of my gain?
Here are the four possible outcomes, along with my gain and the probability:
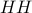 , $2, probability
, $2, probability 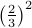 ;
;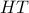 , $0, probability
, $0, probability 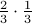 ;
;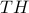 , $0, probability
, $0, probability 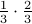 ;
; , -$2, probability
, -$2, probability 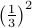 .
.
Hence the expected value is
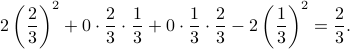
As you would expect, I win more on average if we play the flipping coin bet twice instead of once!
The expected value is linear, in the following sense:
if 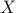 and
and  are two random variables defined on the same
sample space and
are two random variables defined on the same
sample space and 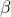 is a real-valued constant, then
is a real-valued constant, then
![mathbb{E}[X+beta Y] = mathbb{E}[X]+betamathbb{E}[Y].](eqs/1564600072536898732-130.png)
Variance
Given a random variable, we can talk about not only the average value (i.e. the expected value), but also how far in general we can expect to be away from the average value. You have probably heard of the term standard deviation in statistics (which is handy for determing your standing in terms of course grades, for example). Like standard deviation, the variance of a random variable measures the spread from the expected value.
Given a random variable 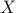 whose output value lies in
whose output value lies in
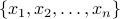 , the variance of
, the variance of 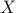 is defined as
is defined as
![mathrm{Var}(X) triangleq mathrm{E}[(X-mathrm{E}[x])^2] = sum_{i=1}^n (x_i-mathbb{E}[X])^2mathrm{Prob}(X=x_i).](eqs/8803623683031416606-130.png)
Example 6
We consider again the scenario in Example 5. We can calculate the variance of my gain:

What this number says is basically that I do have a good chance of losing money!