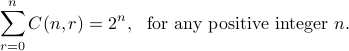Conditional probability and independent events; Bernoulli trial (CSCI 2824, Spring 2015)
Topic covered:
conditional probability
independent events
Bernoulli trial
(Sections 6.2 and 6.3 of the book)
Conditional probability
Often times we are interested in the probability of an event under the assumption that some other event happens. This can be encapsulated by the notion of conditional probability.
Given two events 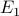 and
and 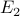 in the same sample space,
the probability of
in the same sample space,
the probability of 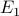 given that
given that 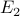 happens is defined as
the ratio
happens is defined as
the ratio
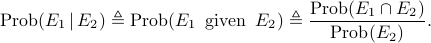
Example 1
Suppose that from a standard deck of 52 playing cards, we draw five cards without ordering. What is the probability of getting a straight flush if one of the cards has to be a diamond 5?
(A straight flush is a set of 5 consecutive cards from the same suit. This excludes the case where we have 10, J, Q, K, A from the same suit (a.k.a. royal flush).)
Note that the probability of getting a straight flush is
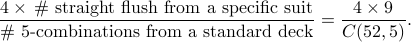
Define the following notations for the two events:
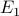 : getting a straight flush;
: getting a straight flush;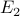 : getting a diamond 5.
: getting a diamond 5.
There are only 5 straight flushes that contain a diamond 5. So
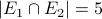 . Hence
. Hence 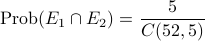 .
.On the other hand,
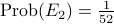 .
.Hence
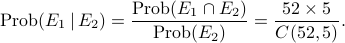
Independent events
Intuitively, we say that two events are independent if the occurrence of one event is independent of the occurrence of the other event. We can formalize this idea using conditional probability.
Two events 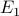 and
and 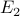 from the same sample spaces are said to
be independent if one of the following conditions holds:
from the same sample spaces are said to
be independent if one of the following conditions holds:
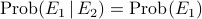 .
.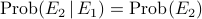 .
.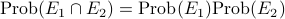 .
.
Simple examples of independent and dependent events:
Experiment: throwing a die for 2 times in a row
Event 1: The first number is even.
Event 2: The second number is even.
These two events are independent.
Experiment: drawing two cards from a deck without replacement
Event 1: One card is a face
Event 2: One card is not a face
These two events are not independent. (See Example 3 below.)
Example 2
Suppose we throw a fair die and draw a card at random from a standard deck. What is the probability that in both cases we get an even number?
The number of possible outcomes where we get an even number in
both cases is 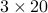 .
.
Hence the required probability is
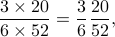
which equals the probability of getting an even number from the die times the probability of getting an even numbered card.
In particular (as we would expect), the events of getting an even number from a die and getting an even numbered card are independent.
Example 3
Suppose we draw two cards from a standard deck without order. Consider the following two events:
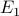 : one card is red.
: one card is red.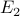 : one card is black.
: one card is black.
Obviously,

On the other hand,
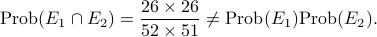
So the two events (in the experiment of drawing two cards) are not independent!
Example 4
Let's say we randomly pick a person from the Colorado population. Of course, exactly one of the following holds for that person:
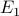 : He/she has lung cancer and is a smoker.
: He/she has lung cancer and is a smoker.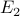 : He/she has lung cancer and is not a smoker.
: He/she has lung cancer and is not a smoker.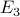 : He/she does not have lung cancer and is a smoker.
: He/she does not have lung cancer and is a smoker.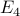 : He/she does not have lung cancer and is not a smoker.
: He/she does not have lung cancer and is not a smoker.
Suppose we know the probability of that a randomly drawn person falls into one of these categories, as follows:
| lung cancer | no lung cancer | |
| smoker | 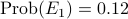 | 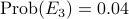 |
| non-smoker | 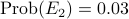 | 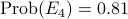
|
While in our example, these probabilities are entirely hypothetical, in real life we do often hear of probabilities as such. They usually are estimates based on statistics drawn from a fraction of the population. We will not go into details on the frequentist approaches in ‘‘estimating’’ the ‘‘probabilities’’ of real life events, but once the ‘‘probabilities’’ are available we can compute conditional probabilities etc.
Then what is the probability that a person has lung cancer given that heshe is a smoker/?
The required probability is
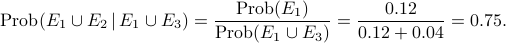
Note that 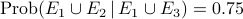 is much bigger than
is much bigger than 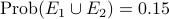 .
.
Bernoulli trials
First we look at an example.
Example 5: flipping a loaded coin multiple times
Suppose we have a loaded coin, where
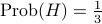 ,
,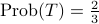 .
.
What is the probability of getting exactly one head in four consecutive flips of the coin?
Note that there are four different outcomes that can produce
exactly one 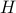 :
:
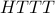 ,
,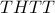 ,
,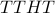 ,
,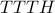 ,
,
each occuring with the probability 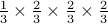 . Hence the probability of
getting one head in four consecutive flips is
. Hence the probability of
getting one head in four consecutive flips is
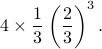
General Bernoulli trials
In general, suppose we perform repeatedly  independent trials,
each of which has exactly two outcomes, success (
independent trials,
each of which has exactly two outcomes, success ( ) and
failure (
) and
failure ( ), with respective probability
), with respective probability
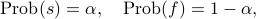
for some ![alphain [0,1]](eqs/7746795350229095261-130.png) . We can talk about the probability
of getting exactly
. We can talk about the probability
of getting exactly 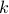 successes out of the
successes out of the  independent
trials — which turns out to depend on the binomial coefficients.
independent
trials — which turns out to depend on the binomial coefficients.
Let 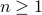 and
and 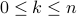 be integers.
The probability of getting exactly
be integers.
The probability of getting exactly 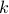 successes in
successes in
 independent trials, each with success probability
independent trials, each with success probability 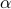 ,
is
,
is
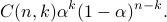
Example 6
We again consider the loaded coin from Example 5.
The probability of getting exactly 4 heads out of 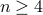 consecutive flips is
consecutive flips is
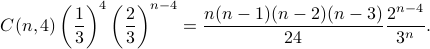
Example 7
Suppose we flip a fair coin 10 times. Then the probability of getting exactly 3 heads is
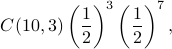
and the probability of getting at most 3 heads is
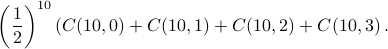
Note that the probability of getting at most 10 heads out of 10 flips is
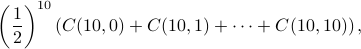
which equals 1 (in line with our intuition) because in general