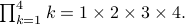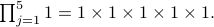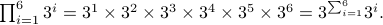Summation (CSCI 2824, Spring 2015)
In this lecture we will cover the basic notation for summation (and product).
Concepts learned:
Summations and summation notation.
Product notation.
Summation
Given a sequence of numbers 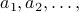 (defined using closed form or a recurrence), we define the summation of the
first
(defined using closed form or a recurrence), we define the summation of the
first  terms of the sequence as
terms of the sequence as
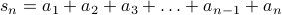
We write this summation succinctly as:
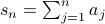
The symbol  (the Greek alphabet Sigma) is the summation operator. The notation
(the Greek alphabet Sigma) is the summation operator. The notation 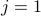 at the bottom of the summation is
the lower limit of the sum and the
at the bottom of the summation is
the lower limit of the sum and the  at the top is the upper limit.
at the top is the upper limit.
Example 1:
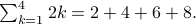
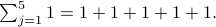
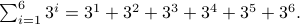
Once again we think in terms of code:
int SumSequence(int n, int [] A){ int j; int sum = 0; for (j=1; j <= n; ++j){ sum = sum + A[j]; } return sum; }
If the sequence 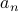 is given, then the summation of its first
is given, then the summation of its first  terms
terms 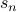 itself
is a sequence given by the following recurrence:
itself
is a sequence given by the following recurrence:
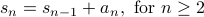
with the base case

Take the sequence 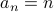 written in the closed form for convenience. What about the
summation of the first
written in the closed form for convenience. What about the
summation of the first  terms of this sequence?
terms of this sequence?
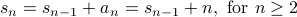
The base case is 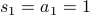 .
.
The closed form for 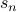 (the summation) is given by
(the summation) is given by
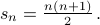
It is really the summation of first  numbers. Here is how the
numbers. Here is how the  year old Gauss supposedly (and famously) reasoned this out:
year old Gauss supposedly (and famously) reasoned this out:
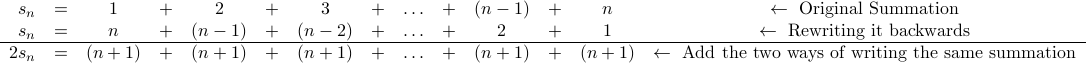
The last equation gives us
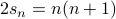
which gives us the required closed form for 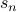 .
.
Observation Getting closed form representations for sequences and summations is often a difficult art in itself. Carl Fredrich Gauss was one of the unrivalled master at this!!
Product
Given a sequence of numbers 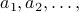 (defined using closed form or a recurrence), we define the
(defined using closed form or a recurrence), we define the
roduct of the
first  terms of the sequence as
terms of the sequence as
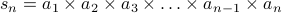
We write this summation succinctly as:
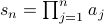
The symbol 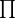 (the Greek alphabet Pi) is the summation operator. The notation
(the Greek alphabet Pi) is the summation operator. The notation 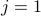 at the bottom of the summation is
the lower limit of the sum and the
at the bottom of the summation is
the lower limit of the sum and the  at the top is the upper limit.
at the top is the upper limit.
Example 1: