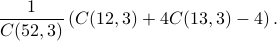Probability: introduction (CSCI 2824, Spring 2015)
Topic covered:
Simple definition of probability
complement rule
mutually exclusive events
sum rule and inclusion-exclusion principle
(Sections 6.1 and 6.2 of the book)
Probability: definition
We often encounter questions like, “what is the probability that I get two cards of the same suit from a standard deck?”, “what is the probability that I get two 6's from rolling a pair of fair dices?”. What exactly do these questions mean? Let's try to understand the notion of probability through a simple example.
Example 1
Suppose that from a standard deck of 52 playing cards, Alicia draws one card (without replacement) and then John draws another. We are interested in the cards that they draw.
The number of possible outcomes is
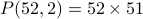 .
.Among all these outcomes, how many outcomes satisfy the condition that the cards that Alicia and John have are from the same suit? The answer would be
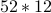 — Alicia draws a card first and she has 52 choices, whereas when John draws a card, in order that his card is from the same suit as Alicia's, he has only 12 choices.
— Alicia draws a card first and she has 52 choices, whereas when John draws a card, in order that his card is from the same suit as Alicia's, he has only 12 choices.
Knowing these two facts, we define the probability of Alicia and John having cards from the same suit to be the ratio:
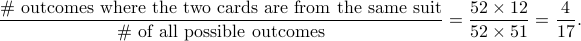
Here we made the implicit assumption that all the outcomes are equally likely. For the most part, in this course we are going to assume that in any experiment, all the outcomes are equally likely.
Probability in terms of sample space and events
In general, we can think of drawing cards, throwing dice, picking a bit string of length 10, etc, as experiments. In any experiment,
the sample space is the set of all possible outcomes, and
an event is simply a subset of the sample space.
(In practice, an event is the collection of outcomes that have some characteristics that we are interested in. )
Given an experiment with a sample space 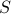 of equally likely outcomes
and an event
of equally likely outcomes
and an event 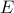 , the probability of the event
, the probability of the event 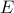 (meaning the probability that
(meaning the probability that 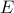 happens) is defined as
happens) is defined as
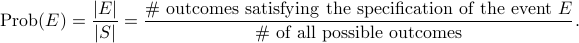
Basic rules
Naturally, in any experiment with sample space  ,
,
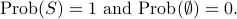
In this course, we deal only with discrete probability (i.e., there are only finitely many possible outcomes). In particular, an event happens with probability 1 if and only if it always happens; an event happens with probability 0 if and only if it never happens.
Complement rule
For any event  ,
,
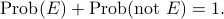
Example 2
Given a group of 20 people born in 1995, what is the probability that at least two of them are born on the same day, assuming that all the birthdays are equally likely?
We can use the complement rule.
Each of the 20 people has a “choice” of 365 birthdays.
So there are
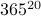 possible birthday “combinations” for these 20 people.
possible birthday “combinations” for these 20 people.Out of these combinations, there are
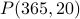 possible outcomes
where no two people share the same birthday.
possible outcomes
where no two people share the same birthday.Therefore the probability that no two people share the same birthday is
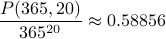 .
.By the complement rule, the probability that at least two people are born on the same day is
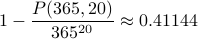 .
.
Mutual exclusiveness and sum rule
Two events 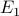 and
and 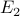 from the same sample space
are said to be mutually exclusive/disjoint if they cannot both happen.
from the same sample space
are said to be mutually exclusive/disjoint if they cannot both happen.
(It means that 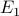 and
and 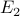 , as sets, are disjoint, i.e.,
they have empty intersection.)
, as sets, are disjoint, i.e.,
they have empty intersection.)
Example 3
If we throw a dice, getting a face-up value 4 and getting a face-up value 3 are mutually exclusive events.
In an experiment where we draw two cards from a deck, the following events are mutually exclusive:
both cards are of the same color.
one card is a spade and the other is a heart.
If two events are mutually exclusive, then the probability that at least one of them happens is the sum of the probability of the individual events.
If two events 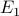 and
and 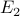 from the same sample space are
mutually exclusive, then
from the same sample space are
mutually exclusive, then
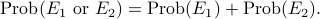
In general, if the two events are not mutually exclusive, we can still
say something about the probability of either 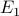 or
or 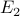 happening,
using the inclusion-exclusion principle.
happening,
using the inclusion-exclusion principle.
If two events 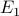 and
and 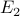 are from the same sample space, then
are from the same sample space, then
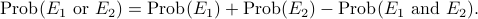
Example 4
Suppose we draw 3 cards from a standard deck without order or replacement. What is the probability that either all three cards are faces (i.e., J, Q, K) or all three cards are from the same suit?
There are
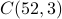 possible outcomes.
possible outcomes.Out of these outcomes, there are
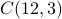 ways of drawing only faces (because there are a total of 12 faces).
ways of drawing only faces (because there are a total of 12 faces).There are
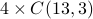 ways to have all three cards from
the same suit.
ways to have all three cards from
the same suit.There are only 4 ways to have all three cards being faces from the same suit.
Therefore the required probability is