Counting unordered lists (CSCI 2824, Spring 2015)
On this page, we consider the problem of counting the number of ordered and unordered lists.
The materials correspond to Sect 5.4 of the textbook.
Recap on counting ordered lists
Example 1
How many ordered lists of 10 letters from 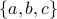 have exactly 3
have exactly 3
 's?
's?
Each subset of
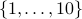 of size 3 corresponds to a possible
placement of the letter
of size 3 corresponds to a possible
placement of the letter  . For instance,
. For instance, 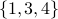 corresponds to
putting
corresponds to
putting  in the 1st, 3rd and 4th position.
in the 1st, 3rd and 4th position. For the remaining 7 spaces, we can put either
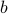 or
or  .
.The number of possible ways to fill the 7 spaces with
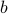 or
or  is
is
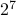 .
.Hence the total number of ordered lists of 10 letters from
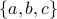 with exactly 3
with exactly 3  's equals
(# ways to put 3
's equals
(# ways to put 3  's among 10 positions) times
(# ways to fill 7 spaces with
's among 10 positions) times
(# ways to fill 7 spaces with 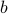 or
or  ), that is,
), that is,
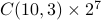 .
.
Example 2
Similarly, the number of ordered lists of 10 English letters with
exactly 3  's is
's is 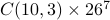 .
.
Counting unordered lists
Example 3
How many ways can I distribute 10 candies among Alice, Bob and Carlos, so that each person has at least 1 candy?
We can reason use the stars and bars diagram.
Start with a list of 10 stars.
Note that each possible distribution can be expressed by putting 2 bars among the stars, so that no bars are at the beginning/end of the lists, and no bars are next to each other.
The insertion of the two bars split the stars into three groups. We can think of the first group representing the candies for Alice, second for Bob and third for Carlos.
For example, ***|***|**** denotes the distribution where Alice gets 3 candies, Bob gets 3 candies and Carlos gets 4 candies.
The number of possible distributions is then equal to the number of possible ways to put 2 bars in 9 spaces, so the answer is
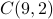 .
.
Example 4
How many ways can I distribute 10 candies among Alice, Bob and Carlos, with the possibility that someone can have no candies?
Consider the following scenario:
We distribute
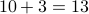 candies among Alice, Bob and Carlos,
so that each person has at least one candy.
candies among Alice, Bob and Carlos,
so that each person has at least one candy.Then we take away one candy from each person. This is equivalent to distributing 10 candies among Alice, Bob and Carlos, where someone can have no candies.
Using the reasoning from Example 3, we see that there are 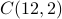 possible ways of distributions.
possible ways of distributions.
Example 5 (NEW!)
How many ways can I distribute 20 candies among Alice, Bob and Carlos, so that each person has at least 3 candies?
To ensure that everyone gets at least 3 candies, we can do the following:
Distribute
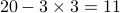 candies among Alice, Bob and
Carlos.
candies among Alice, Bob and
Carlos.There are now 9 candies left!
Give each person 3 candies.
So the number of distinct distributions is equal to the number of ways to distribute 11 candies among 3 people, which is
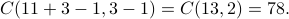
Example 6 (NEW!)
What is the cardinality of the set
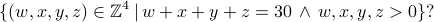
Counting the number of elements of the above set is the same as counting the number of ways to distribute 30 apples among 4 people so that everyone gets at least 1 apple, with:
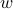 : # apples the 1st person gets
: # apples the 1st person gets : # apples the 2nd person gets
: # apples the 2nd person gets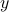 : # apples the 3rd person gets
: # apples the 3rd person gets : # apples the 4th person gets
: # apples the 4th person gets
So then we can use the stars and bars method as in Example 3, and the answer would be
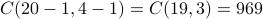 .
.
Example 7 (NEW!)
What is the cardinality of the set
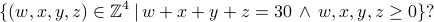
Counting the number of elements of the above set is the same as counting the number of ways to distribute 30 apples among 4 people (though someone could get none), with:
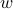 : # apples the 1st person gets
: # apples the 1st person gets : # apples the 2nd person gets
: # apples the 2nd person gets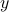 : # apples the 3rd person gets
: # apples the 3rd person gets : # apples the 4th person gets
: # apples the 4th person gets
So then we can use the stars and bars method as in Example 4, and the answer would be
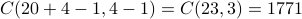 .
.
Example 8 (NEW!)
I have a box of dollar bills. In this box, there are 10 $1 bills, 20 $10 bills and 30 $20 bills. From the box, I grab 5 bills all at onces. How many possible outcomes are there?
Note that I can record all the possible results in a table like this:
| $1 | $10 | $20 |
| 2 | 1 | 1 |
| 1 | 0 | 3 |
 |  | 
|
For instance, the first row says I get two $1 bills, one $10 bill and one $20 bill; the second row says I get one $1 bill and three $20 bills. (I probably should list my results in a more systematic way than the above though!)
Note that in this table each row contains three numbers that sum to 5. The point is that we can think of this counting problem as finding all the possible ways to distribute 5 objects (in this case bills) among 3 different bins.
Hence the answer can be obtained using the stars and bars technique:
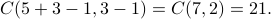
Example 9 (NEW!)
From a big of 8 (identical) red marbles, 5 (identical) green marbles 3 (identical) blue marbles, we grab 4 marbles all at once. How many different outcomes (in terms of color combinations) are there?
Like Example 8, this counting problem is equivalent to counting the number of ways to distribute 4 objects among 3 different bins (for the three different colors), with the restriction that the last bin (for the color green) can hold at most 3 objects.
Without any restriction, there are
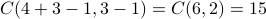 ways to distribute 4 objects in 3
different bins.
ways to distribute 4 objects in 3
different bins.
There is one outcome that we don't want:
that all 4 objects go into the green bin.
Hence the answer is 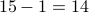 .
.
Placing  objects in
objects in  bins
bins
In general, suppose we have  objects and
objects and  bins, with
bins, with
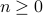 and
and 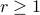 .
Let
.
Let 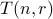 be the number of ways of distributing the
be the number of ways of distributing the  objects in
the
objects in
the  bins.
Then using the above stars-and-bars technique, we get that
bins.
Then using the above stars-and-bars technique, we get that
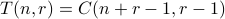 .
.
Note that the number of ways of distributing
 objects in
objects in  bins is also equal to the cardinality of the
following set:
bins is also equal to the cardinality of the
following set:
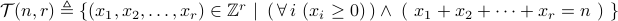 .
.
Finding 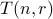 via recursive counting
via recursive counting
We studied how to find 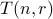 using the stars-and-bar technique.
Now we consider an alternative method: recursive counting.
using the stars-and-bar technique.
Now we consider an alternative method: recursive counting.
Simple cases:
If
 , then all the bins have 0 objects. Hence
, then all the bins have 0 objects. Hence 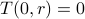 for all
for all
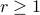 .
.If
 , then there is only one bin for all the objects to go to.
Hence
, then there is only one bin for all the objects to go to.
Hence 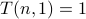 .
.
Now suppose that 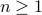 and
and 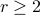 .
We claim that
.
We claim that 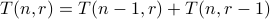 .
.
Consider the number of objects placed in the last bin.
Case 1: nothing is placed in the last bin.
In this case, all the objects are placed in the other
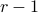 bins.
bins.There are
 ways to place
ways to place  objects
in the first
objects
in the first 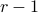 bins.
bins.
Case 2: At least one object is placed in the last bin.
This case is equivalent to trying to place
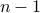 objects in the
objects in the  bins. (After that we place 1 object in the last bin.)
bins. (After that we place 1 object in the last bin.)There are
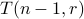 ways to place
ways to place 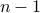 objects in the
objects in the
 bins.
Since the two cases are mutually exclusive and all the placements of
objects must fall under exactly one of the two cases, we have that
bins.
Since the two cases are mutually exclusive and all the placements of
objects must fall under exactly one of the two cases, we have that
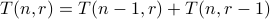 .
.
This is an example of recursive counting. To compute 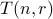 using the recursive formula, we can use the following program:
using the recursive formula, we can use the following program:
int T(int n, int r){ assert( n >= 0 ); assert( r >= 1 ); /* Base Case */ if ( r == 1) return 1; if ( n == 0) return 1; /* Recurrence */ return T(n-1,r) + T(n,r-1); }
Here are the comparison of run times (in seconds) on some instances:
| n | r | Time used by recursion | Time used by explicit formula |
| 20 | 10 | 0.12 s | 1.00e-06 s |
| 30 | 10 | 2.10 s | 1.00e-06 s |
| 40 | 10 | 22.0 s | 1.00e-06 s |