Permutation and Combinations (CSCI 2824, Spring 2015)
This page covers the notions of permutations and combinations. These are structures that do not allow for repetitions.
Permutation
A permutation from  of length
of length  is an
ordered list of length
is an
ordered list of length  whose elements are drawn from
whose elements are drawn from
 without repetitions.
without repetitions.
More generally, given a set 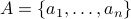 of
of  elements,
a permutation of
elements,
a permutation of 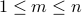 elements is a
sequence of elements
elements is a
sequence of elements  of
of 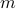 distinct elements chosen from
distinct elements chosen from  :
:
No element can be chosen twice.
The order in which we choose the elements matter.
Eg., What are all the permutations of 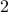 elements chosen from the set
elements chosen from the set 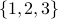 .
Answer:
.
Answer:
1,2
2,1
1,3
3,1
2,3
3,2 This gives rise to 6 permutations.
Number of permutations of length 
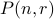 denotes the number of permutations from
denotes the number of permutations from  of length
of length  .
.
(Equivalent notations include  ,
,  ,
, 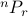 .)
.)
What does the number 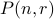 mean?
mean?
 choices for the first element in the permutation.
choices for the first element in the permutation.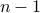 choices for the second.
choices for the second.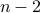 for the third.
for the third.
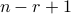 choices for the
choices for the 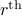 element.
element.
That gives us by product rule 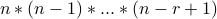 choices overall.
We can write the number
choices overall.
We can write the number 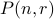 as
as
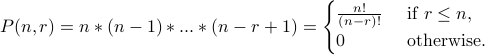 .
.
Here are the some simple examples:
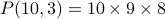 . (3 factors, counting backwards from 10 to 9 to 8.)
. (3 factors, counting backwards from 10 to 9 to 8.)
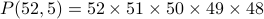 . (5 factors, counting backwards from 52 to 48.)
. (5 factors, counting backwards from 52 to 48.)
Some more examples…
Example 1
How many 4 digit numbers can we form from the digits {1,2,3,7,9}, where we need to use each digit precisely once?
In other words we are looking for a permutation of 4 elements from a set with 5 elements. The answer is 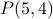 which is
which is
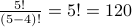 .
.
Example 2
How many four digit numbers can be formed wherein (a) the digits in {1,2,3,7,9} are never used, or (b) if some digit is used it is used multiple times?
Weird problem? But can you find a connection between what is asked in Example 1 and Example 2? Often looking at the complement of a set that we need to count can be easier. :-)
Example 3
Let 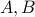 be two sets where
be two sets where  .
How many one-to-one correspondences can exist between
.
How many one-to-one correspondences can exist between  and
and  ?
?
Answer: Let us write  to be
to be 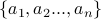 .
Let
.
Let  be the set
be the set 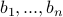 .
.
Choose a permutation of all the
 elements of
elements of  .
.Once the permutation is chosen, link
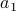 to the first element in the permutation,
to the first element in the permutation, 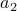 to second,…,
to second,…,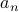 to the
to the 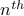 .
.
Each one-to-one correspondence can be formed in this manner.
Therefore there are  functions.
functions.
Question: Let us say professor X says that this is the wrong way to do this. He objects that we did not permute  .
So in his technique:
.
So in his technique:
We take each permutation of
 , each permutation of
, each permutation of  and link the corresponding elements of the permutations.
Thus, he reasons that there should be
and link the corresponding elements of the permutations.
Thus, he reasons that there should be 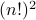 one-to-one correspondences.
one-to-one correspondences.
What is the flaw in his argument?
Combinations
We will now talk about combinations. Note that in permutations the order in which we choose things matter. When doing combinations the order does not matter.
A choice or combination of  elements out of a set with
elements out of a set with  elements is one where
elements is one where
we choose
 elements (by definition, no element can be chosen twice).
elements (by definition, no element can be chosen twice). the order in which we choose things do not matter.
An  -combination from
-combination from  is a subset of
is a subset of  of size
of size  .
.
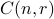 denotes the number of distinct
denotes the number of distinct  -combinations from
-combinations from
 .
.
Equivalent notations include  ,
,
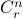 ,
, 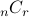 ,
, 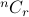 .
.
The formula for 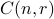 is
is
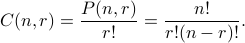
The reason behind 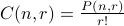 is that we don't care about ordering, and the
is that we don't care about ordering, and the 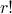 counts the
number of repeated permutations of length
counts the
number of repeated permutations of length  with the same contents. For instance, 125 and 512
are considered the same combination even though they are different permutations; note that there are
with the same contents. For instance, 125 and 512
are considered the same combination even though they are different permutations; note that there are 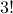 permutations of the three digits 1,2,5.
permutations of the three digits 1,2,5.
Note that in general, whenever 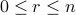 ,
,
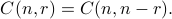
Here are some simple examples:
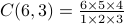 .
.
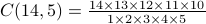 .
.
Example 4
Take the set A ={1,2,3,5}. How many ways are there of choosing a subset with 2 elements?
Obviously, in a subset, we do not care if we choose {1,2} or {2,1} they are the same subset.
Let us first write down the permutations of 2 elements
1,2 and 2,1
1,3 and 3,1
1,5 and 5,1
2,3 and 3,2
2,5 and 5,2
3,5 and 5,3
Now notice that the number of choices in our problem is exactly half the number of permutations.
Since {1,2} is the same as {2,1}
{1,3} is the same as {3,1} and so on.
So the answer should be 6.
Example 5
How many bit strings of length 5 contains exactly two 1's (whose positions are unrestricted)?
We can represent the possible positions of the two 1's as a subset of 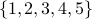 of size 2.
For instance,
of size 2.
For instance,
the subset
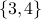 corresponds to the bit string 00110;
corresponds to the bit string 00110;the subset
 corresponds to the bit string 10010; etc.
corresponds to the bit string 10010; etc.
So counting such bit strings boils down to counting the number of subsets of 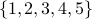 of
size 2, which is
of
size 2, which is 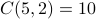 .
.
Example 6
From a group of 10 men and 10 women, how many ways are there to form a committee with 6 members if the committee must have the 2 men and 4 women?
Note that to get the configuration we want, it boils down to picking 2 out of 10 men and 4 out of 10 women.
There are
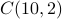 ways to pick 2 out of 10 men.
ways to pick 2 out of 10 men.There are
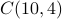 ways to pick 4 out of 10 women.
ways to pick 4 out of 10 women.
Since we have to do both tasks and they can be done independently, using the product rule, the answer is
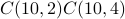 .
.