Introduction to combinatorics (CSCI 2824, Spring 2015)
In this lecture we start the chapter on combinatoics, the art of counting discrete objects.
This page covers the following topics:
Four different types of discrete structures.
Basic counting rules
(Sections 5.1, 5.2 of the textbook)
Recap: Four different structure types in combinatorics
As we saw in the last lecture,
when we talk about counting the number of combinations
of elements from a set  ,
it is very important to identify the following two features:
,
it is very important to identify the following two features:
are we allowed to draw the same element from
 repeatedly?
repeatedly?does it matter which element from
 is drawn first?
is drawn first?
These two features defines four different basic discrete structures relevant to combinatorics:
ordered lists
unordered lists
permutations
combinations
| Ordering matters | Ordering does not matter | |
| Repetitions allowed | Ordered lists | unordered lists |
| Repetitions not allowed | Permutations | Combinations |
Case study: drawing two numbers from 
Today, we consider the following situation: suppose we have a set
 of
of  integers.
integers.
Category 1: Ordered lists
If we draw two integers from  in order and allowing repetition, how many possible outcomes are there?
in order and allowing repetition, how many possible outcomes are there?
This question concerns the number of distinct length-2 ordered lists whose entries are drawn from  .
The possible outcomes that we are interested in can be described by the set
.
The possible outcomes that we are interested in can be described by the set
 .
.
So the answer is simply the cardinality of the set 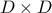 , i.e.,
, i.e.,
 .
.
Category 2: Unordered lists
If we draw two integers from  without order and allowing repetition, how many possible outcomes are there?
without order and allowing repetition, how many possible outcomes are there?
This question concerns the number of distinct length-2 unordered lists whose entries are drawn from  .
The possible outcomes that we are interested in can be described by the set
.
The possible outcomes that we are interested in can be described by the set
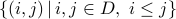 .
.
So the answer is given by the cardinality of this set, which is
 .
.
Category 3: Permutation
If we draw two integers from  in order but not allowing repetition, how many possible outcomes are there?
in order but not allowing repetition, how many possible outcomes are there?
This question concerns the number of permutations of 2 objects from  . The possible outcomes that we are interested in can be described by the set
. The possible outcomes that we are interested in can be described by the set
 .
.
So the answer is given by  .
.
Category 4: Sets
If we draw two inregers from  without order and bot allowing repetition, how many possible outcomes are there?
without order and bot allowing repetition, how many possible outcomes are there?
This question concerns the number of size-2 subsets of  . The possible outcomes that we are interested in can be described by the set
. The possible outcomes that we are interested in can be described by the set
 ,
,
which has  elements.
Hence the answer is
elements.
Hence the answer is  .
.
Basic Rules for Counting
In this section, we mention some basic rules for counting, via set intersection/union. These rules look simple, but knowing how to apply them in practice can be really tricky!
The product rule
If  and
and 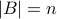 then
then  .
.
More generally, given any sets  ,
,
 .
.
Example 1
We have 3 tee shirts with colors { red, green, blue } and 2 caps with labels {A,B}. How many possible ways are there of choosing a tee shirt and a cap?
Example 2
Let us say that in a tournament teams A, B and C play matches against each other in a round robin. How many matches are played?
How many possible outcomes are there for the tournament?
Solution To count matches is easy, we know that there are three matches to be played M1: A vs. B, M2: A vs. C and M3: B vs. C.
Each match has two outcomes. Winner1 = {A,B}, Winner2 = {A,C}, Winner3 = {B,C}. Therefore, applying the product rule are 2 2 2 = 8 outcomes overall.
The sum rule
If  and
and  are disjoint (i.e.,
are disjoint (i.e.,  ),
then
),
then  .
.
Example 3
We are allowed to make up a positive integer from the digits {1,3,5,7}. Each digit is to be used at most once (we may decide to skip a digit).
example of legal digits are: 13, 1, 3, 137, 7135, ….
Question: How many numbers can we make?
Solution: We split the problem into 4 disjoint counts: count all one digit numbers, two digit numbers, three digit and four digit numbers that can be formed. Together, using the rule of sums, we can simply add these counts and get the required overall count.
One digit numbers: 4 possible choices.
Two digit numbers:
 possible choices.
possible choices.Thee digit numbers:
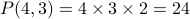 possible choices.
possible choices.Four digit numbers:
 possible choices (remember
possible choices (remember  ).
).
Adding them up we have  possible numbers.
possible numbers.
Inclusion-exclusion principle
We have seen the formula for counting the elements in  when
when  and
and  are disjoint. What if
are disjoint. What if  and
and  are not disjoint,
i.e.,
are not disjoint,
i.e.,  is not an empty set?
is not an empty set?
For any sets  and
and  ,
,
 .
.
Example 4
How many bit strings of length 10 either begin with three 1's or end with two 0's?
Rule of Complements
Let  and
and  be two sets satisfying
be two sets satisfying 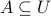 , i.e.,
, i.e.,  is a
subset of
is a
subset of  . Then
. Then
 .
(Here
.
(Here  denotes the set difference
denotes the set difference  minus
minus  ,
i.e.,
,
i.e.,  .)
.)
Example 5
How many odd numbers are there between  and
and  (include both limits in your count).
(include both limits in your count).
Solution First let us just count the even numbers  . Why?
. Why?
46 -> 1 even number
48 -> 2 even numbers
50 -> 3 even numbers
n ->
 even numbers.
even numbers.100 ->
 = 28 even numbers.
= 28 even numbers.
There are a total of  numbers between
numbers between  and
and  .
.
Therefore, odd number count is  .
.
Example 6
Let us say we toss a coin ten times. Each time we toss, we get a head or a tail.
How many possible outcomes are there for the ten tosses?
How many outcomes are there where we see two heads in succession or two tails in succession?