Introduction to combinatorics (CSCI 2824, Spring 2015)
In this lecture we start the chapter on combinatoics, the art of counting discrete objects.
This page covers the following topics:
Counting distinct length-
 binary strings
binary stringsThe product rule
Counting the number of (injective/surjective) functions from a finite set to another finite set
Four different types of discrete structures.
(Sections 5.1, 5.2 of the textbook)
Case study: counting distinct length- binary strings.
binary strings.
Let's consider the simple question: how many distinct binary strings of length 4 are there?
It is not too difficult to list all the possible strings out and count; in this way, we would find out that there are 16 possibilities.
If we change the question a bit, by asking for the number of distinct binary strings of length 100, it would take much longer to obtain the answer (by hand or by using a computer) if we use the same technique, i.e., listing all possibilities and then counting them. A more intelligent method would be to note that, as you probably observed in the previous question, there are two choices (0 or 1) for each bit. So in the previous question, the answer would be
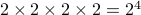 ,
,
each factor corresponding to the choice for one of the four bits.
Similarly, we can expect that the number of distinct
binary strings of length  is
is
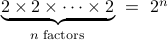 .
.
In particular, the number of distinct binary strings of length 100
would be 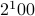 .
.
A takeaway from this case study is that, except for terribly small instances, it can often be very hard to use brute force methods to count the number of objects in a given collection. It is possible, however, to make use of the patterns present in the problem to help us count the number of elements in even very large collection. In this chapter, we will learn how to do just that.
Product rule
One simple and useful rule of counting is the product rule.
Suppose that there are 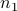 ways to perform task 1, and
there are
ways to perform task 1, and
there are 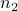 ways to perform task 2.
If tasks 1 and 2 can be performed independently of one another,
then there are
ways to perform task 2.
If tasks 1 and 2 can be performed independently of one another,
then there are 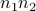 ways to perform task 1 and task 2.
ways to perform task 1 and task 2.
We can apply the product rule to count the number of length  binary strings.
There are two choices for each bit, and we need to make a choice for
each of the
binary strings.
There are two choices for each bit, and we need to make a choice for
each of the  bits. So by the product rule, there are
bits. So by the product rule, there are 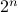 choices.
choices.
Case Study: number of distinct functions from a finite set to another finite set
Suppose we have two nonempty finite sets  and
and  , with
, with
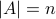 and
and 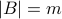 .
.
What is the number of distinct functions from  to
to  ?
?
By definition, any function
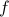 from
from  to
to  must send each element of
must send each element of  to exactly one element of
to exactly one element of  .
. In other words, for each element
 of
of  , we have to choose
one out of the
, we have to choose
one out of the 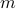 elements in
elements in  as the output of
as the output of  under the function
under the function 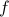 .
. Since
 has
has  elements, by the product rule there would be
elements, by the product rule there would be  different functions from
different functions from
 to
to  .
.
What is the number of distinct injective functions from  to
to  ?
?
Let's say
 and
and 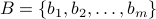 .
(Note that for a set, the elements are always distinct, so e.g.
.
(Note that for a set, the elements are always distinct, so e.g. 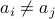 for distinct
for distinct 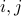 !)
!)Then for any function
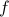 , there must be some
, there must be some 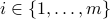 such that
such that
 .
.If
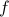 is injective, then
is injective, then 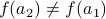 , that is,
, that is,  can only be chosen
from
can only be chosen
from 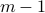 elements of
elements of  .
.Inductively, we get that for any integer
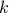 bewteen 2 and
bewteen 2 and  ,
if
,
if 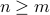 and we have already fixed the values of
and we have already fixed the values of 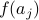 for
for
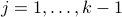 , then there are
, then there are  different choices for the value
different choices for the value  .
.Using the product rule, we get that there are a total of
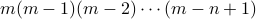 distinct injective functions from
distinct injective functions from  to
to  .
.
Note that if 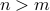 , one of the factors in
, one of the factors in 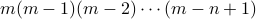 would be zero.
so there would be no injective function from
would be zero.
so there would be no injective function from  to
to  . This agrees with what we learned
in Chapter 4, that
. This agrees with what we learned
in Chapter 4, that
if  is injective, then
is injective, then  .
.
Four different structure types in combinatorics
Very often, we are given a set  , and we are
interested in counting the number of combinations
of elements from
, and we are
interested in counting the number of combinations
of elements from  with certain features.
with certain features.
In the example of bit strings, we take combinations from the elements of
 .
The ordering of the elements does not matter,
and repetitions are allowed.
.
The ordering of the elements does not matter,
and repetitions are allowed.In the example of functions from
 to
to  ,
we take combinations
of
,
we take combinations
of  .
.
When we talk about counting the number of combinations
of elements from a set  ,
it is very important to identify the following two
features:
,
it is very important to identify the following two
features:
are we allowed to draw the same element from
 repeatedly?
repeatedly?does it matter which element from
 is drawn first?
is drawn first?
These two features defines four different basic discrete structures relevant to combinatorics:
ordered lists
unordered lists
permutations
combinations
| Ordering matters | Ordering does not matter | |
| Repetitions allowed | Ordered lists | unordered lists |
| Repetitions not allowed | Permutations | Combinations |
In the next lecture, we will study these four structures in depth.