Growth of divide-and-conquer recursion: master theorem (CSCI 2824, Spring 2015)
In this lecture we introduce the divide-and-conquer recursions, and the master theorem for estimating the growth of divide-and-conquer recursions.
(Section 4.8 of the textbook)
A divide-and-conquer recursion is a recursive sequence 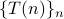 of the form
of the form
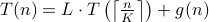 ,
, 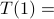 some positive constant,
some positive constant,
where 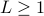 ,
, 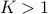 and
and 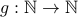 .
Loosely speaking, a divide-and-conquer recursion captures
the number of operations involved by a divide-and-conquer algorithm
applied on a specific problem. As a recursive algorithm,
divide-and-conquer proceeds by repeatedly breaking the current problem
down into smaller subproblems of the same nature,
until it is small enough that the solution is “trivial”.
.
Loosely speaking, a divide-and-conquer recursion captures
the number of operations involved by a divide-and-conquer algorithm
applied on a specific problem. As a recursive algorithm,
divide-and-conquer proceeds by repeatedly breaking the current problem
down into smaller subproblems of the same nature,
until it is small enough that the solution is “trivial”.
Simple examples of divide-and-conquer include binary search and merge sort.
Each specialized divide-and-conquer algorithm would have the following few features:
the work that needs to be done to split the problem into smaller subproblems of the same nature — the amount of such work is captured by the function
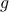 ;
;the number
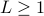 of subproblems that need to be solved after each
break-down;
of subproblems that need to be solved after each
break-down;the size of each subproblem, usually given by
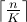 or
or
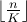 .
(It is very common to drop the floor or ceiling in the
expression for the recursion
.
(It is very common to drop the floor or ceiling in the
expression for the recursion 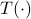 , by abuse of notation.)
, by abuse of notation.)
With the roles of 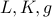 in mind, it is not difficult to understand
the intuition behind the divide-and-conquer recusion.
For more information on divide-and-conquer algorithms,
see e.g. the Wikibook chapter.
in mind, it is not difficult to understand
the intuition behind the divide-and-conquer recusion.
For more information on divide-and-conquer algorithms,
see e.g. the Wikibook chapter.
What we are interested in is the growth of divide-and-conquer
recursions: the growth of such a recursion tells us the efficiency
of the corresponding divide and conquer algorithm. It turns out that
the growth of 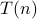 depends on whether the function
depends on whether the function 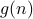 grows
faster, at the same rate or slower than the polynomial function
grows
faster, at the same rate or slower than the polynomial function
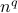 , where
, where 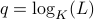 .
.
Consider the recursive function 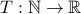 defined by
defined by
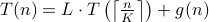 ,
, 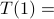 some positive constant,
some positive constant,
with 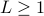 ,
, 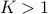 and
and 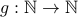 .
.
Define 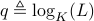 . Then the following is true.
. Then the following is true.
Case 1: If
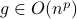 for some
for some 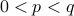 , then
, then 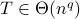 .
.Case 2: If
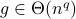 , then
, then 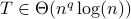 .
.Case 3: If
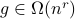 for some
for some 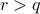 , then
, then 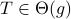 .
.
Example 1
We estimate the growth rate of the recursive function
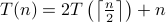 .
.
Take
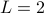 ,
, 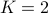 ,
, 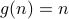 .
.Then
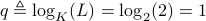 .
.Note that
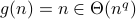 .
.Hence we end up with Case 2, i.e.,
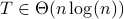 .
.
Example 2
We estimate the growth rate of the recursive function
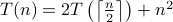 .
.
Take
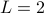 ,
, 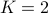 ,
, 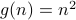 .
.Then
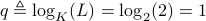 .
.Note that
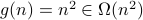 .
.Hence we end up with Case 3, i.e.,
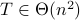 .
.
Example 3
We estimate the growth rate of the recursive function
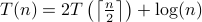 .
.
Take
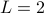 ,
, 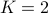 ,
, 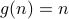 .
.Then
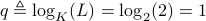 .
.Note that
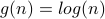 grows slower than
grows slower than 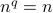 .
.Hence we end up with Case 1, i.e.,
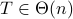 .
.
Example 4
We estimate the growth rate of the recursive function
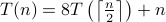 .
.
Take
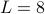 ,
, 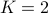 ,
, 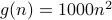 .
.Then
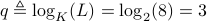 .
.Note that
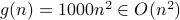 , so
, so 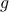 grows slower than
grows slower than 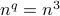 .
.Hence we end up with Case 1, i.e.,
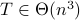 .
.