Equivalence relations (CSCI 2824, Spring 2015)
In this lecture, we will revise some of the concepts on relations that we covered previously.
Reflexive, Symmetric and Transitive Relations.
Partial and Total Orders.
Then we will look into equivalence relations and equivalence classes. We will see how an equivalence on a set partitions the set into equivalence classes.
Revision
Let us make sure we understand key concepts before we move on. To do so, take five minutes to solve the following problems on your own. You are welcome to discuss your solutions with me after class.
All these problems concern a set
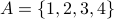 .
. Relation
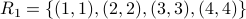 .
.Relation
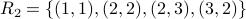 .
.Relation
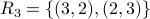 .
.Relation
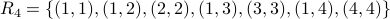 .
.Relation
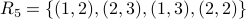 .
.Relation
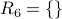 (empty relation).
(empty relation).
| ID |  | 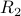 | 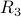 | 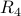 | 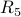 | 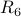 |
| Reflexive? | ||||||
| Symmetric? | ||||||
| Transitive? | ||||||
| Irreflexive? | ||||||
| Anti-Symmetric? |
Equivalence Relation
An equivalence relation 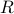 over a set
over a set  is a reflexive, symmetric and transitive relation.
is a reflexive, symmetric and transitive relation.
Which of the following are examples of equivalence relations over 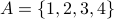 .
.
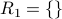 .
. 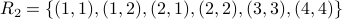 .
. 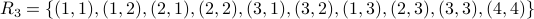 .
.
Just check that the relations above are reflexive, symmetric and transitive.
 fails to be reflexive.
fails to be reflexive. is an equivalence relation.
is an equivalence relation.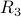 is also an equivalence relation.
is also an equivalence relation.
Example-1
The relation 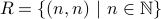 is an equivalence relation.
is an equivalence relation.
The Cartesian product of any set  with itself is a relation
with itself is a relation 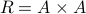 . All possible tuples exist in
. All possible tuples exist in 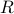 . This relation is also an
equivalence.
. This relation is also an
equivalence.
Modular-Congruences
For any number 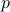 , we have an equivalence relation
, we have an equivalence relation 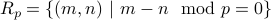 .
.
Often we denote 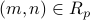 by the notation
by the notation 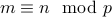 (read as
(read as 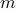 and
and  are congruent modulo
are congruent modulo 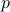 ).
).
Verify that 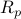 is an equivalence for any
is an equivalence for any 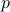 .
.
Reflexivity:
For all 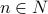 , we have that
, we have that 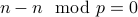 . Therefore
. Therefore 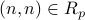 .
.
Symmetry:
Clearly if 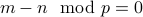 then
then 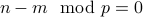 .
.
Transitivity:
If 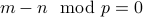 and
and 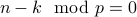 then
then
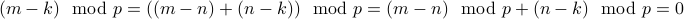 .
.
Equivalence Classes
We now look at how equivalence relation on  partitions the original set
partitions the original set  .
.
Let us take the set 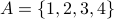 . And the equivalence
. And the equivalence 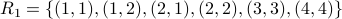 .
.
Let us collect everything that  is equivalent to. This gives us the set
is equivalent to. This gives us the set 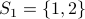 . Collecting everything equivalent to
. Collecting everything equivalent to
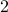 again gives us
again gives us 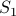 . Collecting everything that
. Collecting everything that  is equivalent to gives us
is equivalent to gives us 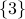 and similarly for
and similarly for 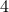 , we get
, we get
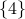 .
.
Therefore, 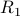 is said to induce the following partition of the set
is said to induce the following partition of the set  :
:
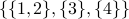
What is the partition induced by the equivalence: 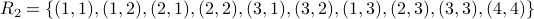 ?
?
To answer this, consider:
![[1]_{R_2} = { 1, 2, 3 }](eqs/6867707439879604022-130.png)
![[2]= [1]](eqs/1789396274426912256-130.png)
![[3] = [1]](eqs/3285072328312995026-130.png)
![[4] = { 4 }](eqs/1295216738764136806-130.png) .
.
The partition induced by 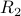 is therefore:
is therefore: 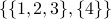 .
.
The equivalence class of an element 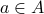 under an equivalence relation
under an equivalence relation 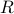 is denoted as
is denoted as ![[a]_R](eqs/6993857433414924609-130.png) .
.
![[a]_R = { b | (a,b) in R](eqs/5090210748191339942-130.png)
If 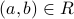 then
then ![[a]_R = [b]_R](eqs/641113069680375969-130.png) .
.
Let 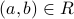 . We show that
. We show that ![[a]_R subseteq [b]_R](eqs/5715969076454931020-130.png) and vice versa,
and vice versa, ![[b]_R subseteq [a]_R](eqs/3750311350644546256-130.png) .
.
To show that ![[a]_R subseteq [b]_R](eqs/5715969076454931020-130.png) , let
, let ![x in [a]_R](eqs/4141458168215641796-130.png) . We have
. We have 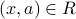 . Since
. Since 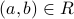 , we conclude by
transitivity of
, we conclude by
transitivity of 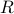 that
that 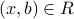 . Therefore
. Therefore ![x in [b]_R](eqs/7141659169330643443-130.png) .
.
The proof of ![[b]_R subseteq [a]_R](eqs/3750311350644546256-130.png) is very similar. Therefore
is very similar. Therefore ![[a]_R = [b]_R](eqs/641113069680375969-130.png) represent the same equivalence classes.
represent the same equivalence classes.
We now show that two equivalence classes are either the same or disjoint.
Whenever ![[a]_R cap [b]_R not= emptyset](eqs/205083878323404960-130.png) then
then ![[a]_R = [b]_R](eqs/4559142337538910358-130.png) .
.
{Proof}
Let ![c in [a]_R cap [b]_R](eqs/8238542414210551961-130.png) . We have
. We have 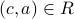 and
and 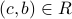 . Therefore by symmetry and transitivity of
. Therefore by symmetry and transitivity of 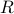 ,
we conclude that
,
we conclude that 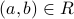 . Therefore
. Therefore ![[a]_R = [b]_R](eqs/641113069680375969-130.png) .
.
This shows that given any set  , and equivalence relation
, and equivalence relation 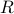 , the equivalence classes
, the equivalence classes
![{ [a]_R | a in A }](eqs/4706201442706703783-130.png)
is a partition of the set  :
:
If
![[a]_R not= [b]_R](eqs/6400268444184955348-130.png) , we conclude that
, we conclude that ![[a]_R cap [b]_R = emptyset](eqs/2045031113887648193-130.png) .
. ![bigcup_{ain A} [a]_R = A](eqs/5162374949868464005-130.png) .
.