Growth of functions (CSCI 2824, Spring 2015)
In this lecture we learn some very important notions concerning the growth of functions:
big O notation
big Theta notation
big Omega notation
(Section 4.8 of the textbook)
Studying the growth of functions is an important part of the analysis of algorithms.
Take a look at the two codes below:
for (i=0; i < n; ++i){ sleep(1); /*-- Sleep for one second --*/ }
For 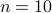 , the program takes roughly
, the program takes roughly 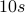 to run.
Contrast the program above with this one:
to run.
Contrast the program above with this one:
for (i=0; i < n; ++i){ for (j=0; j < n; ++j){ sleep(0.01); /*-- sleep 10 milli seconds --*/ } }
For 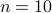 , the program above takes
, the program above takes 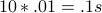 to run.
Comparing the expected running times of the programs:
to run.
Comparing the expected running times of the programs:
| n | Linear | Quadratic | Comparison |
| 10 | 10 | .1 | 100x speedup |
| 100 | 100 | 100 | same |
| 1000 | 1000 | 10,000 | 10x slowdown |
| 10000 | 10000 | 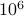 | 100x slowdown |
As  increases, the quadratic loop gets slower and slower than the linear loop.
increases, the quadratic loop gets slower and slower than the linear loop.
Let us increase the delay in each linear loop iteration to 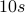 and
decrease the delay in quadratic loop to
and
decrease the delay in quadratic loop to  milli seconds (0.001 s).
How does the table above change??
milli seconds (0.001 s).
How does the table above change??
The linear loop's running time for given input  is roughly
is roughly 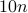 seconds and
the quadratic loop is
seconds and
the quadratic loop is 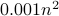 . But for
. But for 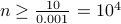 , the
linear loop will once again be faster than the quadratic and remain so for larger
values of
, the
linear loop will once again be faster than the quadratic and remain so for larger
values of  .
.
Running Time Complexity of Algorithms
There are two basic rules we follow when comparing running times or analyzing running times of algorithms.
We only care about trends as input size tends to
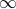 . In other
words, the performance of algorithms often varies unpredictably for
small input sizes. So we only care about the time complexity as they
grow larger.
. In other
words, the performance of algorithms often varies unpredictably for
small input sizes. So we only care about the time complexity as they
grow larger.
We do not care about constant factors: Algorithm implementation on x86 machine with 2 GHz clock frequency and 8 GB RAM may be much slower than a machine with 1 GHz clock and 4 GB RAM. But this slowdown often is a constant factor. It will roughly be some factor say
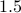 times
faster on the faster processor. But we do not care about these
constant factors.
times
faster on the faster processor. But we do not care about these
constant factors.
In terms of trends, we say that the linear loop in the example above
has a running time complexity of 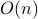 (pronounced Big-OH of
(pronounced Big-OH of  or
Order
or
Order  ). And quadratic loop above has a complexity of
). And quadratic loop above has a complexity of 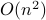 .
.
Informally, 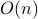 can refer to running times that could in reality be
any number of functions including:
can refer to running times that could in reality be
any number of functions including:
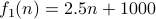
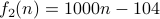 or
or 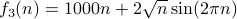 .
. 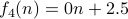 .
.
All we care about in these functions is that: as  grows larger and
larger, beyond
grows larger and
larger, beyond 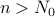 for some large number
for some large number 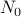 , the dominant
term in the function is
, the dominant
term in the function is  with a constant factor in front of
it. The remaining terms matter less and less as
with a constant factor in front of
it. The remaining terms matter less and less as  increases, and
eventually stop being the dominant terms.
increases, and
eventually stop being the dominant terms.
Let us now define the Big-OH notation.
Given a function 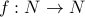 , and
, and 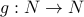 we write
we write 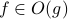 iff there exists a number
iff there exists a number 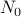 such that for all
such that for all 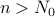 ,
,
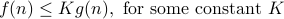
Note that 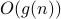 denotes a set of functions which satisfy the definition above.
denotes a set of functions which satisfy the definition above.
In other words, we have that asymptotically as 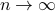 ,
,
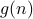 grows at least as fast as
grows at least as fast as 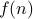 (if not faster) as
(if not faster) as 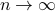 .
.
Eg., we have 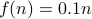 being in the set
being in the set 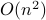 . Beyond
. Beyond 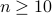 , we see that
, we see that
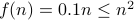 .
.
Is
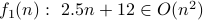 ?
? Is
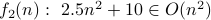 ?
? 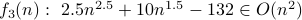 ?
? what are all the functions in
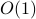 ?
?
Let us now answer these questions.
Yes. We have for
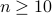 , we have
, we have 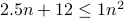 . Therefore,
. Therefore, 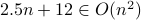 .
.Yes. Once again, for
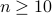 , we have
, we have 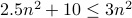 . Therefore,
. Therefore, 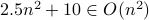 .
.No. No matter, how high we set the constant
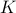 , we
, we 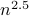 , the dominant term of
, the dominant term of 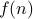 cannot be domainted by
cannot be domainted by 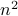 .
.A function
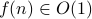 if eventually for some
if eventually for some 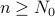 ,
, 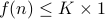 . Therefore, any function that is
eventually upper bounded by a constant will be in
. Therefore, any function that is
eventually upper bounded by a constant will be in 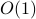 . Examples include:
. Examples include: 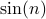 ,
, 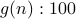 ,
, 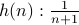 , and so on.
, and so on.
Example # 2.
Is 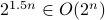 ?
?
This is an interesting question. Can we find a constant 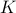 such that
such that 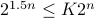 for all
for all 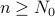 ?
To understand, let us call
?
To understand, let us call 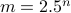 . We have
. We have 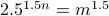 . We are asking the question if
. We are asking the question if 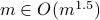 ? The answer is no.
? The answer is no.
Is 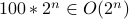 ?
?
Once again, let us call 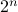 as
as 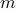 . We are asking now if
. We are asking now if 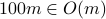 , and the answer is yes.
, and the answer is yes.
Is 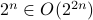 ?
?
Again, let us call 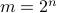 . We have
. We have 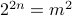 . We are asking if
. We are asking if 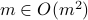 . The answer is yes.
. The answer is yes.
Big-Omega and Big-Theta
Just like Big-Oh, we can define Big-Omega 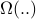 to denote lower bounds.
to denote lower bounds.
We say that 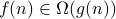 if and only if there is a
if and only if there is a 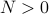 and a constant
and a constant 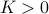 such that
such that
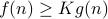
In other words, informally we say that the function  is lower bounded asymptotically by
is lower bounded asymptotically by 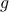 (upto a constant factor).
(upto a constant factor).
Exampls
1. 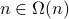
We can choose 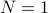 and
and 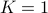 . We conclude (trivially) that
. We conclude (trivially) that 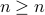 for all
for all 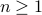 .
.
2. 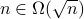 .
.
We can choose 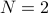 and
and 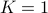 , we conclude that
, we conclude that 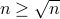 for all
for all 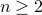 .
.
3. What are all the functions in 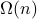 , give a succinct description?
, give a succinct description?
Any function whose growth is super-linear. Examples include 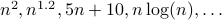 .
.
4. Is the following function in 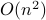 ? Is it in
? Is it in 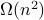 ?
?
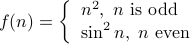
Since we are concerned about the asymptotics of the function: for the
upper bound we should focus on 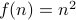 when
when  is odd.
Therefore,
is odd.
Therefore, 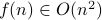 . But for lower bound, we should look at
. But for lower bound, we should look at
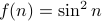 when
when  is even. Therefore
is even. Therefore 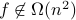 .
.
We say that 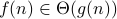 if
if 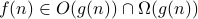 .
.
It is common to write 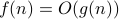 or
or 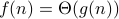 often instead of
often instead of 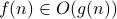 . But the latter is more sound since
. But the latter is more sound since 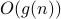 strictly speaking is not a function but a set of functions that are all upper bounded by
strictly speaking is not a function but a set of functions that are all upper bounded by 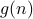 .
.