Cardinality of sets (CSCI 2824, Spring 2015)
In this lecture we will talk about:
Cantor's Diagonalization Argument: No one-to-one correspondence between a set and its powerset.
Degrees of infinity: Countable and Uncountable Sets.
Countable Sets: Natural Numbers, Integers, Rationals, Java Programs (!!)
Uncountable Sets: Real Numbers, Functions over naturals,…
What all this means for computers.
(Section 4.3 of the textbook)
Comparing sizes using correspondences
We defined the cardinality of a finite set is the number of elements of that set. In general, we can define cardinality for infinite sets too.
Two sets 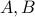 have the same cardinality if and only if there is a one-to-one correspondence
have the same cardinality if and only if there is a one-to-one correspondence 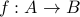 .
.
Example-1
Let us say that a chef needs to make sure she has enough dinnerware for her guests. She does not need to count plates, knives, forks and so on. All she needs to do is to arrange the plates, knives, forks and so on along side each other neatly to see if there is a one-to-one correspondence.
Example-2
We established a one-to-one correspondence between natural numbers and odd numbers.
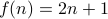 .
.
We can do the same for 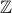 the set of integers and
the set of integers and 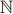 the natural numbers.
the natural numbers.
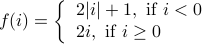
Example-3
Let us now establish a one-to-one correspondence between natural numbers 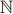 and the set
and the set 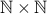 . We just
need to line up elements of
. We just
need to line up elements of 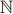 and
and 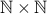 just like our chef does to knives and forks.
just like our chef does to knives and forks.
Cantor's Diagonalization Argument
We will now prove that no set can have the same cardinality as its power set.
Claim: The set of natural numbers 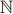 cannot be put in a one-to-one correspondence with its power set
cannot be put in a one-to-one correspondence with its power set 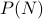 .
.
Proof
We will prove by contradiction by assuming that such a correspondence exists between 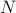 and its power set
and its power set 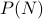 .
.
Suppose there is a one-to-one and onto function 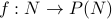 . We note that
. We note that 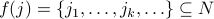 .
We can represent
.
We can represent  by the following table.
by the following table.
| 1? | 2? | 3? | … | n? | … | |
| f(1) | 1 | 0 | 1 | … | 0 | …. |
| f(2) | 0 | 1 | 0 | … | 1 | …. |
| . . . | …. | |||||
| f(n) | 0 | 1 | 0 | …. | 0 | …. |
| ... | … |
Each row represents the set 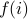 and for every
and for every 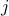 , a “1” entry in (i,j) says that
, a “1” entry in (i,j) says that 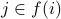 . A “0” entry says that
. A “0” entry says that 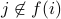 .
.
We will now prove that  is not onto by constructing
is not onto by constructing 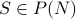 such that
such that 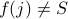 for all
for all 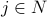 . In other words,
the set
. In other words,
the set 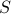 we construct will not be mapped onto.
we construct will not be mapped onto.
The idea is to construct 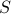 so that we go down the table and “spoil” each
so that we go down the table and “spoil” each 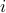 as follows:
as follows:
Take a look at diagonal entries
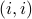 in the table for all
in the table for all 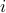 .
. If entry (i,i) has a 1 in it we make sure that
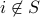 . If it has a zero in it, we add
. If it has a zero in it, we add 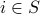 .
.
We now claim that 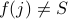 for all
for all 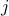 . Suppose it were, we know that either (1)
. Suppose it were, we know that either (1) 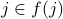 or (2)
or (2) 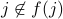 .
.
If
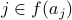 then we know that
then we know that 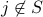 . Therefore,
. Therefore, 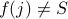 .
.If
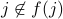 then
then 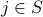 . Again, once again
. Again, once again 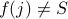 .
.
By making sure that the set 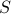 we construct disagrees with all
we construct disagrees with all 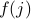 , we establish that the function
, we establish that the function  cannot be onto.
cannot be onto.
Therefore, the natural numbers cannot have the same cardinality as 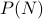 . In fact, we have
established an argument to say that
. In fact, we have
established an argument to say that 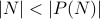 by showing that any function
by showing that any function 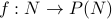 cannot
be onto.
cannot
be onto.
Claim For every set  , there can be no one-to-one correspondence (bijection) between
, there can be no one-to-one correspondence (bijection) between  and
and 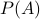 .
.
This can be proved by extending the “diagonalization” argument to
arbitrary sets  .
.
Suppose, for the sake of contradiction, 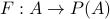 is a
one-to-one correspondence. We will contradict by construction a
set
is a
one-to-one correspondence. We will contradict by construction a
set 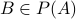 such that no
such that no 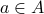 maps onto to
maps onto to 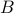 .
.
For every 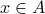 , we consider the question if
, we consider the question if 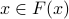 . If yes,
we set
. If yes,
we set 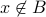 . Otherwise,
. Otherwise, 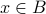 .
.
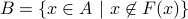 .
.
Since 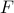 is a one-to-one and onto function,
is a one-to-one and onto function, 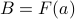 for some
for some 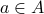 .
.
Is 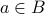 ?
?
If yes, then 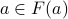 therefore by construction,
therefore by construction, 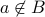 .
.
If not, then 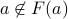 and therefore,
and therefore, 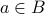 by our construction.
by our construction.
Either way, we get a contradiction.
Countable and Uncountable Sets
A set is countable if it can be placed in one-to-one correspondence with the natural numbers.
A set is uncountable if it can be placed in one-to-one correspondence with a set such as 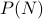 (or in general, any set known not
to be in one-to-one correspondence with
(or in general, any set known not
to be in one-to-one correspondence with 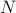 ).
).
Cantor-Schroeder-Bernstein Theorem
We will use the following important lemma to make the process of establishing one-to-one correspondences easier.
Claim For any two sets 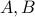 if there is a one to one function
if there is a one to one function 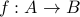 and a one-to-one function
and a one-to-one function 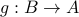 then
there is a one-to-one onto function (a one-to-one correspondence, in other words)
then
there is a one-to-one onto function (a one-to-one correspondence, in other words) 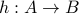 . (Therefore
. (Therefore 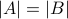 ).
).
The proof for finite sets is easy. Since  exists, we conclude that
exists, we conclude that 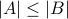 . On the other hand, from the existence of
. On the other hand, from the existence of
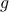 we conclude that
we conclude that 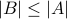 . Combining, we conclude that
. Combining, we conclude that 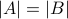 . For finite sets, this is enough to show that
a one-to-one correspondence function
. For finite sets, this is enough to show that
a one-to-one correspondence function 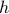 also exists.
also exists.
Real Numbers
Claim The set of real numbers in the in the interval ![[0,1]](eqs/5113014419904972428-130.png) has a one-to-one correspondence with
has a one-to-one correspondence with 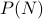 (the power set of natural numbers).
(the power set of natural numbers).
Proof We will prove by using CSB theorem above by establishing one-to-one functions:
One-to-one function
 between
between ![[0,1]](eqs/5113014419904972428-130.png) and
and 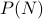 .
.One-to-one function
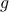 between
between 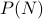 and
and ![[0,1]](eqs/5113014419904972428-130.png) .
.
Let us first write down the function ![f: [0,1] rightarrow P(N)](eqs/6755531817913546255-130.png) . The basic idea is that we take any number with the decimal expansion
. The basic idea is that we take any number with the decimal expansion
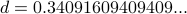 and have a set of the form
and have a set of the form 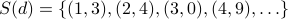 that describes the decimal expansion. A
tuple
that describes the decimal expansion. A
tuple 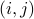 in
in 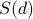 says that the
says that the 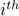 position has the number
position has the number 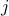 in it. However,
in it. However, 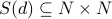 . So we do a second
trick called Godel Numbering. We represent each tuple
. So we do a second
trick called Godel Numbering. We represent each tuple 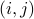 by a single number
by a single number 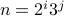 .
.
Therefore the One-to-one function  constructs the decimal expansion for a given input
constructs the decimal expansion for a given input ![d in [0,1]](eqs/6788286630818841523-130.png) and derives the set
and derives the set 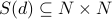 . Next
it Godel numbers the elements of
. Next
it Godel numbers the elements of 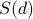 to give a set
to give a set 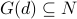 .
.
Let us now take care of the one-to-one function 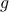 between
between 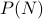 and
and ![[0,1]](eqs/5113014419904972428-130.png) . Take a set
. Take a set 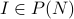 .
. 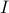 is a set of natural numbers say
is a set of natural numbers say
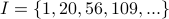 . We construct a number
. We construct a number 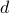 in binary of the form
in binary of the form 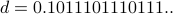 where the
where the 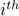 position after the fixed point
has a
position after the fixed point
has a  if
if 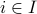 and a
and a 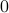 otherwise. We can verify in class that this gives a one-to-one mapping from
otherwise. We can verify in class that this gives a one-to-one mapping from 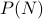 to reals
to reals 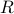 .
.
Here is the flaw in the construction: the function 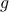 is not one-to-one. The problem is that the decimals
is not one-to-one. The problem is that the decimals 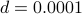 and
and 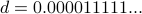 mean the same thing. In fact an infinite
sequence of trailing
mean the same thing. In fact an infinite
sequence of trailing  s is forbidden in binary number scheme. The reason
s is forbidden in binary number scheme. The reason 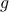 is not one-to-one is because two sets map onto
is not one-to-one is because two sets map onto 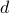 :
:
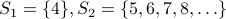
How can we fix this flaw?
Simple, instead of binary, we interpret the number in decimal. We have 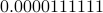 to be a perfectly valid decimal number that is not the same as
to be a perfectly valid decimal number that is not the same as
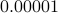 . Therefore, to fix the proof, we just interpret the number
. Therefore, to fix the proof, we just interpret the number 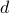 in decimal as opposed to binary.
in decimal as opposed to binary.
Since we have one-to-one mapping both ways, we conclude from CSB theorem that there is some one-to-one correspondences. In other words,
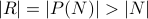 .
.
Rational Numbers
We show that the set of rational numbers 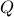 is countable. By showing a one-to-one correspondence between
is countable. By showing a one-to-one correspondence between 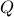 and
and 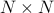 .
.
Using CSB theorem, we instead show a one to one function 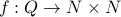 and a function
and a function 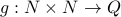 .
.
As a clarification, we note that rational numbers are numbers of the form 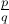 where
where 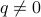 . There are many representations
for a rational number. Eg.,
. There are many representations
for a rational number. Eg., 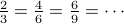 all represent the same element of
all represent the same element of 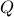 q. We will use the lowest terms representations where
q. We will use the lowest terms representations where
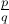 do not have prime factors in common.
do not have prime factors in common.
Let us first derive the map 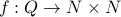 . Given a rational number
. Given a rational number 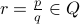 in its lowest terms, we simply say
in its lowest terms, we simply say 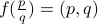 .
This map has to be one-to-one (it is not onto, but we do not need that since we are using CSB theorem).
.
This map has to be one-to-one (it is not onto, but we do not need that since we are using CSB theorem).
Claim The function  is one-to-one.
is one-to-one.
The proof is very simple, can you try?
We now define the map 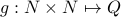 as
as 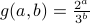 .
.
Claim We claim that 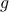 is one-to-one.
is one-to-one.
Proof Let us assume that 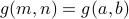 for some
for some 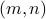 and
and 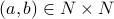 . We aim to prove that
. We aim to prove that
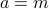 and
and 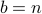 .
.
Therefore 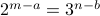 . Therefore,
. Therefore, 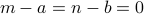 , or
, or  and
and 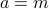 (since
(since 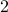 and
and  are
relatively prime numbers).
are
relatively prime numbers).