Function Composition and Inverse (CSCI 2824, Spring 2015)
In this lecture we look at the following topics:
Inverses of functions and relations
Composition of functions and relations
Invertibility of functions.
Inverses
We will first talk about inverse relations. Let 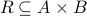 be a relation. Its inverse is defined as
be a relation. Its inverse is defined as
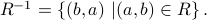
Note that 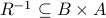 . In other words, we flip the domain and co-domain of R. We also flip the tuples
in
. In other words, we flip the domain and co-domain of R. We also flip the tuples
in 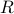 . I.e., if
. I.e., if 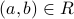 then
then 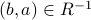 and vice versa.
and vice versa.
Example
As an example, write down the inverse of the following relation:
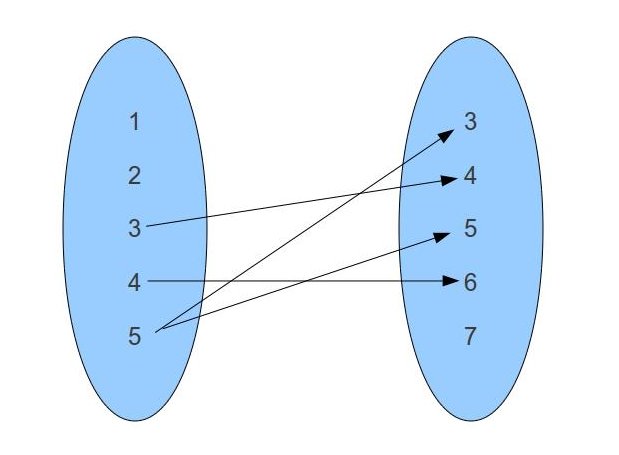 |
Example-2
Consider the relation 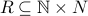 defined as
defined as 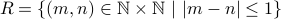 .
Show that
.
Show that 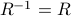 .
.
To show that, we will first show that if 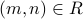 then
then 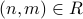 .
.
Let 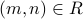 . We have
. We have 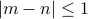 . Therefore,
. Therefore, 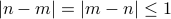 . Therefore, if
. Therefore, if 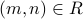 then
then 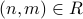 .
.
Now, it is easy to show that (a) 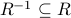 and (b)
and (b) 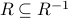 .
.
Inverse of a Function
The inverse of a function is always a relation. On the other hand, the inverse of a function need not always be a function. For the figures below, say whether the function represented has an inverse or not.
 |
The top left function has an inverse. The others do not. |
We can look at graphs of functions to check if an inverse exists. Does the function depicted below have an inverse?
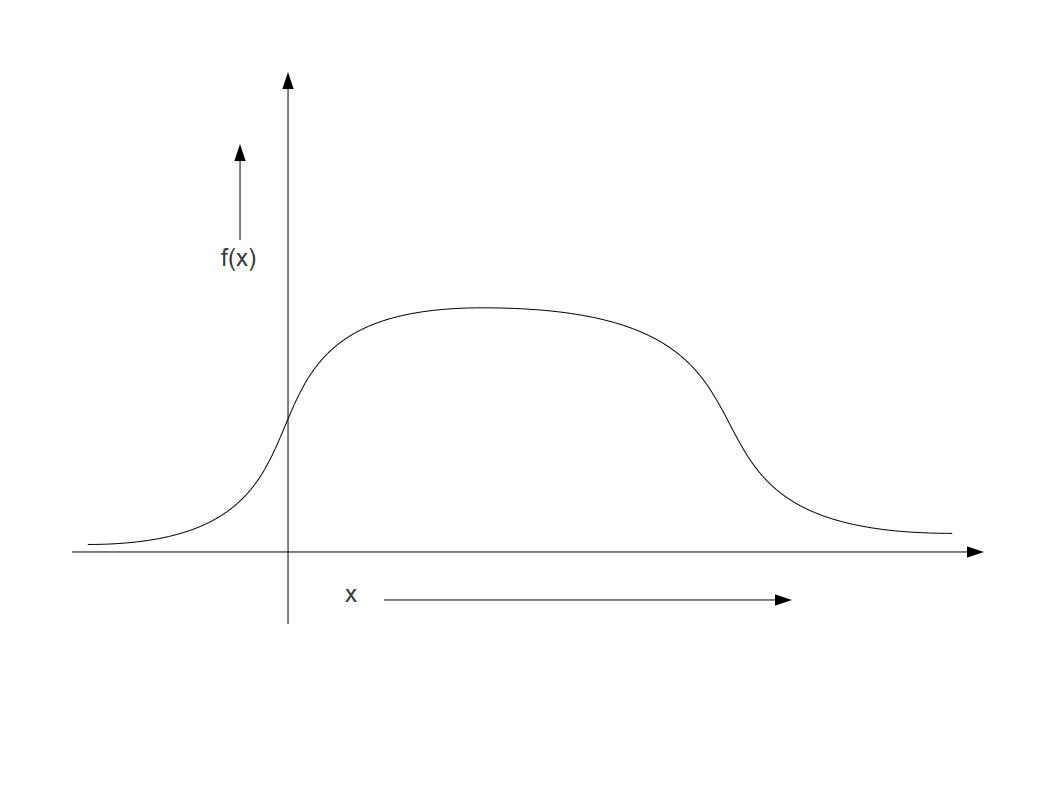 |
We will expand on these topics when we learn about one-to-one and onto functions in the next lecture.
Compositions of Relations and Functions
Given two functions or two relations, we can talk about the functional and relational compositions, respectively.
Function Composition
Let us take two functions 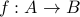 and
and 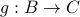 . Function composition captures the application of
. Function composition captures the application of
 followed by
followed by 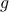 to get a new function
to get a new function 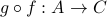 , defined by
, defined by
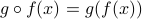
The order of composition is important. Please note.
Examples of Function Composition
We will now do some examples.
Example 1
Take 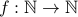 where
where 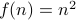 and
and 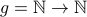 with
with 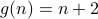 .
.
What is 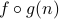 and
and 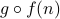 ? Explain the difference by writing them out in closed form.
? Explain the difference by writing them out in closed form.
Answer  says that we first apply
says that we first apply 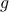 to
to  and then apply
and then apply  on the result. Therefore we obtain
on the result. Therefore we obtain 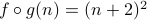 .
.
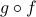 says that we first apply
says that we first apply  and then apply
and then apply 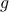 to yield
to yield 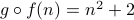 .
.
The order of composition can be really confusing.
Relation Composition
Relation composition is similar to function composition. It is an important operation in databases and is therefore called a join of two relations in database jargon.
Let 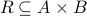 and
and 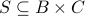 be two relations. We say that the composition
be two relations. We say that the composition
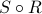 of
of 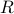 and
and 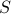 is a relation
is a relation 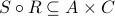 such that
such that
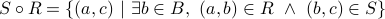
The picture below provides an illustration:
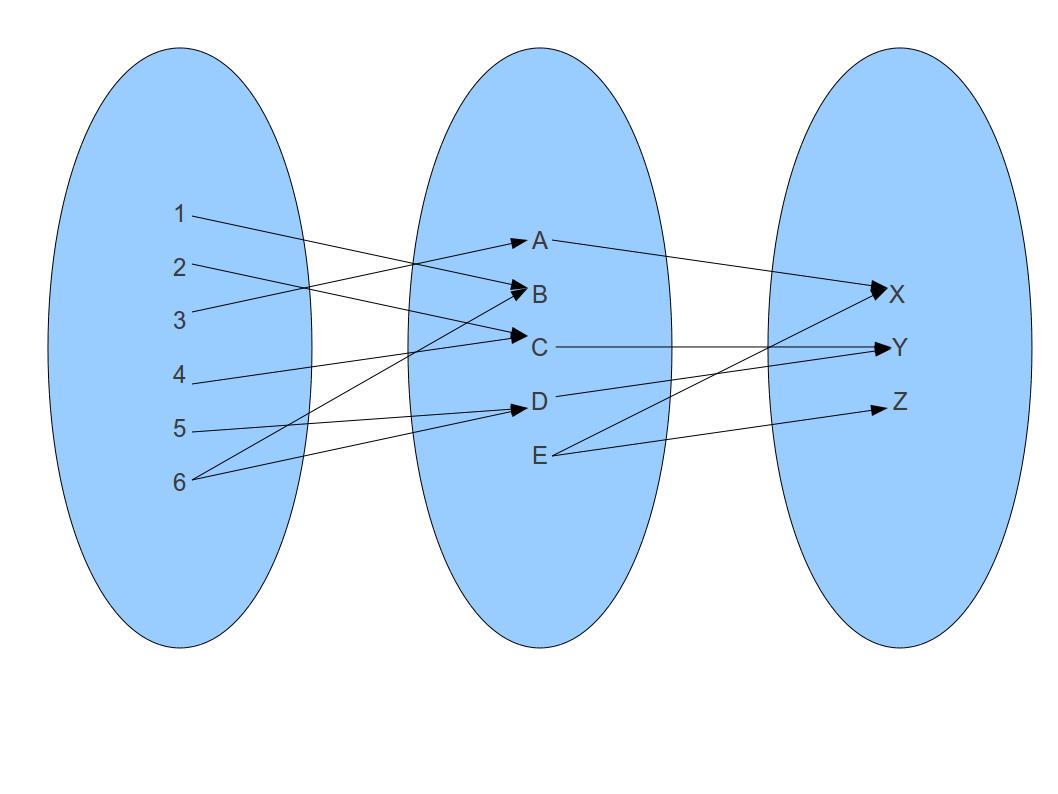 |
We see that 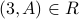 and
and 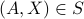 . Therefore
. Therefore 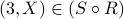 .
What other tuples exist in
.
What other tuples exist in 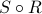 ?
?
Answer 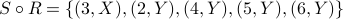 .
.
Example-2
Suppose we provide a social network between people in the class in the form of the Friends relation, where
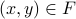 iff
iff 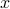 is a friend of
is a friend of 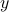 . How do we find friends of friends?
. How do we find friends of friends?
Answer Simply do 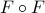 .
.
Example-3
Suppose we have a relation 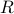 on movie stars wherein
on movie stars wherein 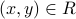 signifies that person
signifies that person 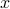 and
and 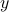 acted in the same film
together. We wish to find out all people with six degrees of separation from Kevin Bacon. How do we do that?
acted in the same film
together. We wish to find out all people with six degrees of separation from Kevin Bacon. How do we do that?
The answer is to find the relation
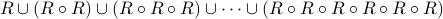
Invertibility of Functions
Let us now investigate the question of invertibility of
functions. Suppose 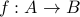 is a function from
is a function from  to
to 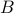 ,
under what conditions does
,
under what conditions does  have an inverse function?
have an inverse function?
Informally we can say the following:
 cannot map many elements of
cannot map many elements of  to the same element of
to the same element of 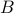 .
.  cannot leave any element of
cannot leave any element of 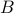 unmapped to.
unmapped to.
 |
Therefore, we define the following properties of functions:
 is one-to-one (injective) if
is one-to-one (injective) if  maps every element of
maps every element of  to a unique element in
to a unique element in 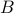 . In other words no element of
. In other words no element of 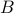 are mapped to by two or more elements of
are mapped to by two or more elements of  .
.  is onto (surjective)if every element of
is onto (surjective)if every element of 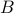 is mapped to by some element of
is mapped to by some element of  . In other words, nothing is left out.
. In other words, nothing is left out.  is one-to-one onto (bijective) if it is both one-to-one and onto. In this case the map
is one-to-one onto (bijective) if it is both one-to-one and onto. In this case the map  is also called a one-to-one correspondence.
is also called a one-to-one correspondence.