Some examples on proving/disproving a function is injective/surjective (CSCI 2824, Spring 2015)
This page contains some examples that should help you finish Assignment 6.
(See also Section 4.3 of the textbook)
Proving a function is injective
Recall that a function 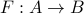 is injective/one-to-one if
is injective/one-to-one if
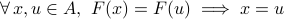 .
.
To prove that a function
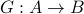 is injective, we start by: “fix any
is injective, we start by: “fix any 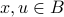 with
with 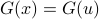 ”
Then (using algebraic manipulation etc) we show that
”
Then (using algebraic manipulation etc) we show that  .
.To prove that a function
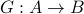 is not injective, we demonstrate two explicit elements
is not injective, we demonstrate two explicit elements 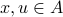 and show that
and show that 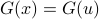 .
.
Example 1: Disproving a function is injective (i.e., showing that a function is not injective)
Consider the function
 .
.
(This function defines the Euclidean norm of points in 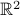 .)
Recall also that
.)
Recall also that 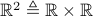 .
.
Claim: 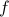 is not injective.
is not injective.
Note that 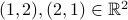 are distinct and
are distinct and
 . Hence
. Hence 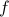 is not injective. QED.
is not injective. QED.
Example 2: Proving a function is injective
Consider the function
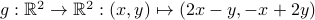 .
.
Claim: 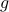 is injective.
is injective.
Fix any
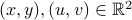 satisfying
satisfying 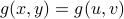 .
.By definition of
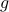 , we have
, we have 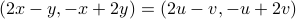 .
.The equality of the two points in
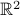 means that their
coordinates are the same, i.e.,
means that their
coordinates are the same, i.e.,
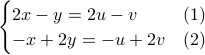
Multiplying equation (2) by 2 and adding to equation (1), we get
 .
.Then
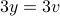 , or equivalently,
, or equivalently, 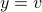 .
.On the other hand, multiplying equation (1) by 2 and adding to equation (2), we get
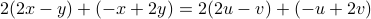 , or equivalently,
, or equivalently,  .
.Therefore
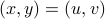 .
. This proves that
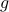 is injective. QED.
is injective. QED.
Proving a function is surjective
Recall that a function 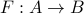 is surjectiveonto if
is surjectiveonto if
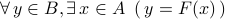 .
.
To prove that a function
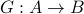 is surjective, we proceed as follows:
is surjective, we proceed as follows: Fix any
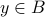 .
.(Scrap work: look at the equation
 . Try to express
. Try to express  in terms of
in terms of 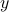 .)
.)Write something like this: “consider
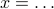 .” (this being the expression in terms of
.” (this being the expression in terms of 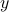 you find in the scrap work)
Show that
you find in the scrap work)
Show that 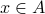 . Then show that
. Then show that 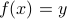 .
.
To prove that a function
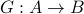 is not surjective, simply argue that some element of
is not surjective, simply argue that some element of  cannot possibly be the
output of the function
cannot possibly be the
output of the function 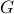 .
.
Example 3: disproving a function is surjective (i.e., showing that a function is not surjective)
Consider the function
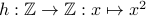 .
.
Claim: 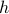 is not surjective.
is not surjective.
Consider
 .
. Suppose on the contrary that there exists
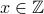 such that
such that
 , i.e.,
, i.e., 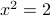 .
.Then
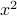 being even implies that
being even implies that  is even,
i.e.,
is even,
i.e., 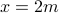 for some integer
for some integer 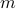 .
. Then
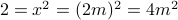 , implying that
, implying that 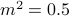 ,
which is impossible because
,
which is impossible because 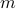 is an integer and
the square of an integer must also be an integer.
is an integer and
the square of an integer must also be an integer.Hence there does not exists
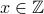 such that
such that
 .
.This shows that
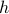 is not surjective. QED.
is not surjective. QED.
Example 4: disproving a function is surjective (i.e., showing that a function is not surjective)
Consider the absolute value function
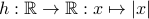 .
.
Claim: 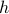 is not surjective.
is not surjective.
Note that for any
 in the domain
in the domain 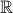 ,
, 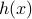 must be nonnegative.
must be nonnegative.On the other hand, the codomain
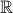 includes negative numbers.
includes negative numbers.Hence
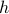 is not surjective.
is not surjective.
Example 5: proving a function is surjective
Consider again the function
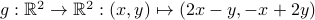 .
.
Claim: 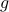 is injective.
is injective.
Fix any
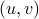 in the codomain
in the codomain 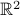 .
.We want to find a point
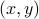 in the domain satisfying
in the domain satisfying 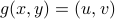 .
.Note that
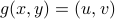 if and only if
if and only if 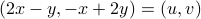 .
.This is equivalent to
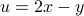 and
and 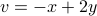 .
.We are going to express
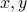 in terms of
in terms of 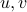 .
.Note that the first equation implies
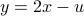 .
. Substituting this into the second equation, we get
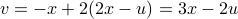 .
. Rearranging to get
 in terms of
in terms of 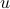 and
and  , we get
, we get
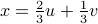 .
.Now we work on
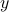 . The second equation gives
. The second equation gives 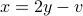 .
. Substituting into the first equation we get
 .
.Rearranging to get
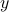 in terms of
in terms of 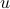 and
and  , we get
, we get
 .
.Hence the input we want is
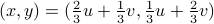 .
.
Fix any
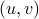 in the codomain
in the codomain 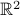 .
.Consider
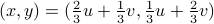 .
.Note that
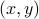 lies in the domain
lies in the domain 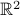 and
and
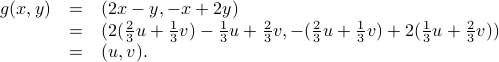
This shows that
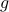 is surjective.
is surjective.
Finding the inverse
Once we show that a function is injective and surjective, it is easy to figure out the inverse of that function. The inverse is simply given by the relation you discovered between the output and the input when proving surjectiveness.
Only bijective functions have inverses!
If we are given a bijective function  , to figure out the inverse of
, to figure out the inverse of 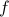 we start by looking at
the equation
we start by looking at
the equation 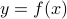 . Then we perform some manipulation to express
. Then we perform some manipulation to express  in terms of
in terms of 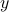 .
.
Example 6
Consider the function
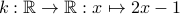 .
.
We claim (without proof) that this function 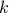 is bijective. So what is the inverse of
is bijective. So what is the inverse of 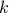 ?
?
Fix any
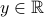 .
.Consider the equation
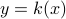 and we are going to express
and we are going to express  in terms of
in terms of 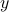 .
.Using the definition of
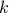 , we get
, we get  , which is equivalent to
, which is equivalent to  .
.Therefore the inverse of
 is given by
is given by
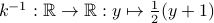 .
.
Example 7
The function
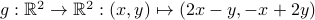
that we consider in Examples 2 and 5 is bijective (injective and surjective). The inverse is given by
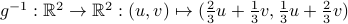 .
.
Note that this expression is what we found and used when showing 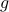 is surjective.
is surjective.