Functions and Relations (CSCI 2824, Spring 2015)
This page covers the following concepts.
Determining whether a function is injective
Determining whether a function is surjective
Proving a function is injective/surjective
These topics can be found in Section 4.3 of the textbook.
Injective and surjective functions
Recall the definition of injective and surjective functions.
A function 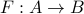 is said to be
is said to be
injective (or one-one) if for any distinct
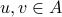 ,
, 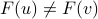 ;
;surjective (or onto) if for any
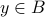 ,
, 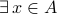 such that
such that 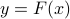 .
.bijective if
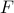 is both injective and surjective.
is both injective and surjective.
More descriptively,
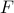 is injective if
is injective if 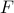 maps every element of
maps every element of  to a unique element in
to a unique element in 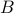 .
In other words no element of
.
In other words no element of 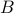 are mapped to by two or more elements of
are mapped to by two or more elements of  .
. 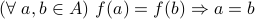 . (This is the contrapositive of the implication we have in the definition.)
. (This is the contrapositive of the implication we have in the definition.)
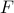 is surjective if every element of
is surjective if every element of 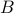 is mapped to by some element of
is mapped to by some element of  .
In other words, nothing is left out.
.
In other words, nothing is left out.
Example 1
Classify the following functions 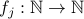 between natural numbers as one-to-one and onto.
between natural numbers as one-to-one and onto.
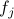 | One-to-One? | Onto? |
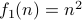 | Yes | No |
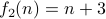 | Yes | No |
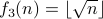 | No | Yes |
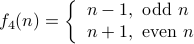 . . | Yes | Yes |
It helps to visualize the mapping for each function to understand the answers.
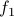 is not onto because it does not have any element
is not onto because it does not have any element  such that
such that 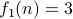 , for instance.
, for instance.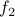 is not onto because no element
is not onto because no element  such that
such that 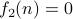 , for instance.
, for instance.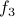 is not one-to-one since
is not one-to-one since 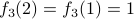 .
.
Guessing whether a function 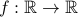 is injective/surjective
is injective/surjective
If a given function has both the domain and codomain being the set of real numbers 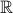 ,
then one visual way of guessing whether that function is injective/surjective can be done by using the graph.
We imagine swiping a horizontal rule up or down and the number of intersection this horizontal rule makes with the graph.
,
then one visual way of guessing whether that function is injective/surjective can be done by using the graph.
We imagine swiping a horizontal rule up or down and the number of intersection this horizontal rule makes with the graph.
A function is injective if and only if the horizontal rule intersects the graph at most once at any fixed
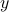 -value.
-value.A function is surjective if and only if the horizontal rule intersects the graph at least once at any fixed
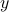 -value.
-value.
(As an aside, the vertical rule can be used to determine whether
a relation is well-defined: at any fixed 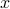 -value, the vertical
rule should intersect the graph of a function with domain
-value, the vertical
rule should intersect the graph of a function with domain 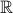 exactly once.)
exactly once.)
Proving that a function is injective/surjective
Let 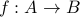 be a function.
be a function.
To prove that
 is injective, we proceed like this…
is injective, we proceed like this…Let
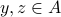 be such that
be such that 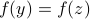 .
.Infer from the equality
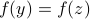 and use the definition
of
and use the definition
of  to show that
to show that 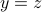 .
.
To prove that
 is surjective, we proceed like this…
is surjective, we proceed like this…Fix any
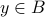 .
. Consider the equality
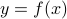 and express
and express 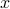 in terms of
in terms of 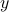 .
.Double check: plug in your expression for
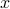 into
into  ,
and evaluate
,
and evaluate 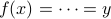 .
.
Example 2
Prove that the function 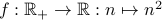 is one-to-one.
is one-to-one.
Fix any
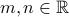 with
with 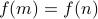 .
. Then
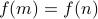 implies that
implies that 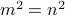 .
. Then
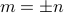 .
. Splitting cases on
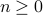 , we have
, we haveFor
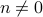 ,
, 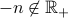 ,
therefore
,
therefore 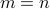 for this case.
for this case. For
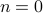 , we have
, we have 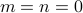 .
.
Therefore, it follows that
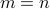 for both cases.
for both cases.This proves that
 is one-to-one. QED.
is one-to-one. QED.
Example 3
Prove that the function
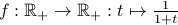 is injective.
is injective.
Fix any
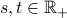 with
with 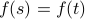 .
.Then
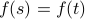 implies that
implies that 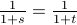 .
.Inverting the fractions on both sides of the equality, we get
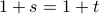 .
.Canceling 1 on both sides, we get
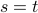 .
. This proves that
 is injective. QED.
is injective. QED.
Example 4
Prove that the function 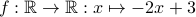 is surjective.
is surjective.
Fix any
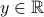 .
.Consider the equality
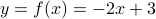 . Expressing
. Expressing 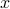 in terms of
in terms of 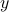 ,
we get
,
we get 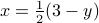 .
.Now note that
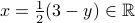 and
and
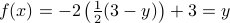 .
.This shows that
 is surjective. QED.
is surjective. QED.
Example 5
Prove that the function 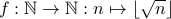 is onto.
is onto.
Fix any
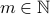 .
.Then
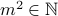
and
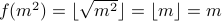 .
.Therefore, all
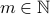 are mapped onto.
are mapped onto.Hence
 is onto. QED.
is onto. QED.