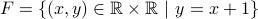Functions and Relations (CSCI 2824, Spring 2015)

This page covers the following concepts.

Review of relations and functions
More examples and non-examples on functions
Injective (one-one) functions
Surjective (onto) functions
Bijective functions

These topics can be found in Sections 4.1 and 4.3 of the textbook.

Recap on the definitions

We recall some definitions we learned last time.

Relation

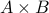A (binary) relation from a set to another set is a subset of Atimes B .

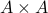A (binary) relation on a set is a subset of Atimes A .

Function

A function from a set to another set is a relation from to that satisfies the condition

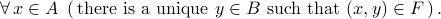
forall, xin A left(, text{there is a unique }yin Btext{ such that } (x,y)in F,right).

The set here is called the domain of and is called the codmain of .

More concretely, we can think of functions as taking input from the domain and assign to that input something that lies in the codomain.

A function is also called a map, or a mapping.

Different ways to express a function

Usually, we write function as an assignment, emphasizing that it takes a certain input and assign a value to that input via some rule. We use the notation 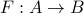F: Ato B to denote a function with domain and codomain .

More specifically, there are at least three different ways of expressing the assignment rule of the same function.

Example 1

Consider the update of any real number by incrementing 1. There are three different ways of expressing this as a function on 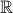mathbb{R} .

More examples and non-examples of functions

We review some examples and non-examples of functions.

Example 2

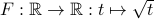Consider F:mathbb{R}tomathbb{R} : tmapsto sqrt{t} .

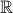is not a function because is not defined for every number in the domain mathbb{R} . (E.g. F(-1)=sqrt{-1} is undefined as a real number.)

On the other hand, if we restrict the domain to the set of all nonnegative real numbers 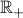$mathbb{R}_+$ :

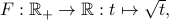
$F:mathbb{R}_+tomathbb{R} : tmapsto sqrt{t},$

then is in fact a function.

Example 3

Consider the relation

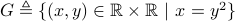$G triangleq {(x,y)inmathbb{R}times mathbb{R} | x=y^2}$ .

This relation is not a function because for the input 1 has two different output 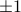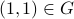pm1 : (1,1)in G and (1,-1)in G .

The relation

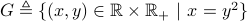$G triangleq {(x,y)inmathbb{R}times mathbb{R}_+ | x=y^2}$ .

is not a function either, because e.g. 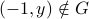(-1,y)notin G , as seen in Example 2.

Finally the relation

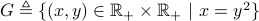$G triangleq {(x,y)inmathbb{R}_+times mathbb{R}_+ | x=y^2}$ .

is a function.

Pre-image and image of a function

Image

The image of a function 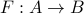F:Ato B is the set {F(x) | xin A} , that is, the set of all possible outputs of the function .

Image and preimage of a subset under a function

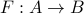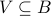Let F:Ato B be a function, Usubseteq A and Vsubseteq B .

The image of under the function is the set

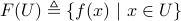F(U) triangleq { f(x) | xin U} .

The pre-image of 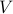under the function is the set

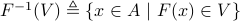$F^{-1}(V) triangleq { x in A | F(x)in V}$ .

Injective and surjective functions

Injective, surjective and bijective functions

A function 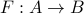F:Ato B is said to be

injective (or one-one) if for any distinct , ;
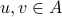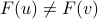surjective (or onto) if for any 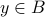, 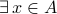such that .
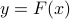bijective if is both injective and surjective.

More descriptively,

is injective if maps every element of to a unique element in . In other words no element of are mapped to by two or more elements of .
- .
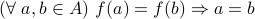is surjective if every element of is mapped to by some element of . In other words, nothing is left out.