Functions and Relations (CSCI 2824, Spring 2015)
In this section, we learn the notion of relations, functions and well-definedness.
This is part of Sect 4.1 of the book.
Functions
We have already encountered functions many times and we often use functions when we program. Let us formalize what functions are in mathematical terms:
A function 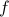 from a set
from a set  to a set
to a set  is
associates (or maps) every element of the set
is
associates (or maps) every element of the set  to some element of
the set
to some element of
the set  . We express the fact that a function
. We express the fact that a function 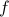 maps
maps  to
to  as
as 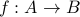 .
.
Example -1
Consider 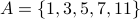 and
and 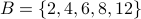 . Consider function
. Consider function  .
.
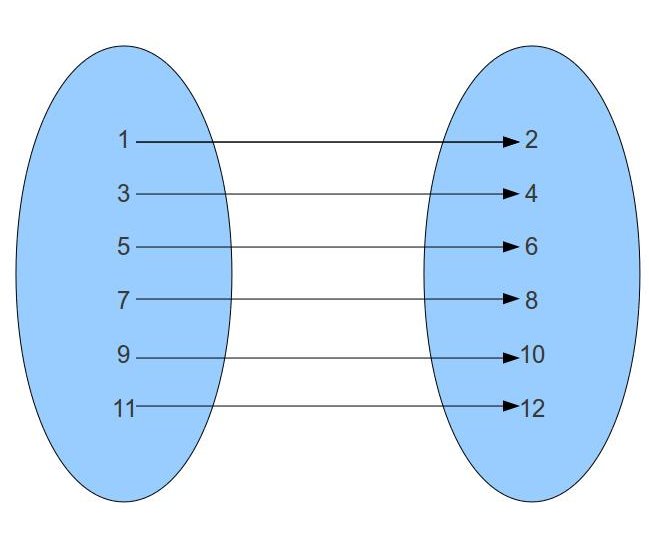 |
The function above can be represented explicitly by the mapping
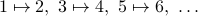
or implicitly by the rule/formula  .
.
Example-2
Functions can map many elements of  to the same element of
to the same element of  . But the rule is that each element of
. But the rule is that each element of  can only be mapped to one element of
can only be mapped to one element of  .
Which of the following are functions?
.
Which of the following are functions?
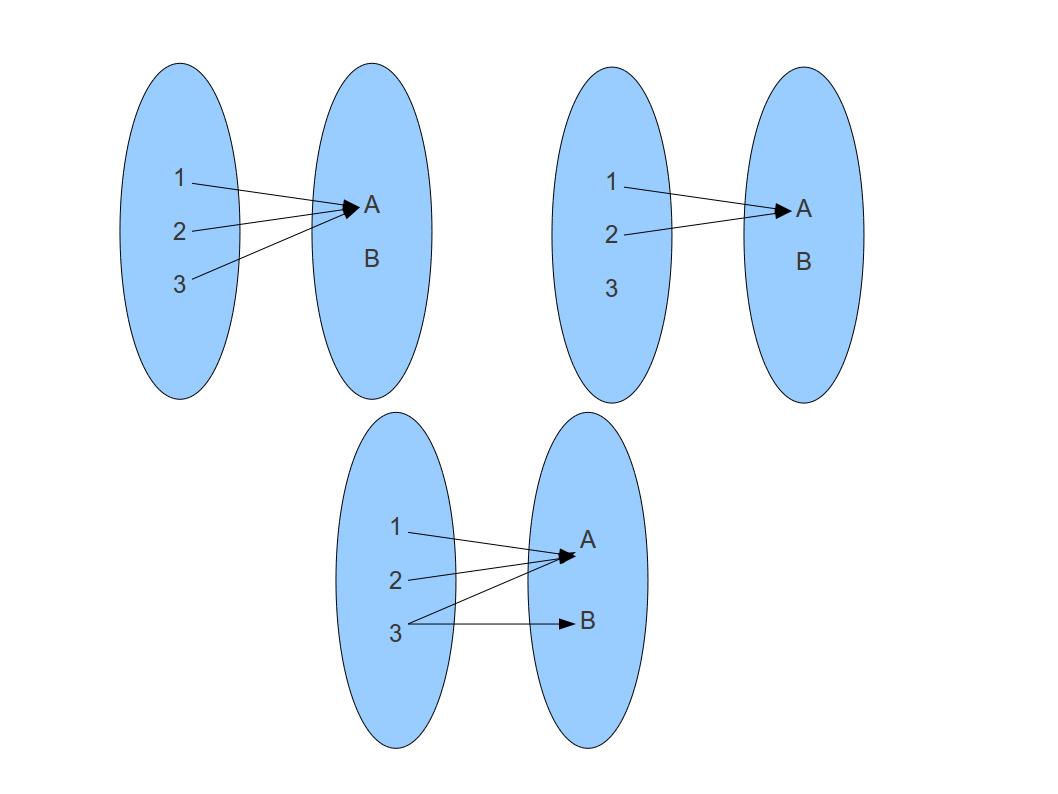 |
Example-3: Power Set Signature
While discussing power sets, we mentioned a correspondence between
power-sets of a set and binary strings. We can indeed write it as a
function. Let us take  to be
to be 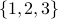 and
and 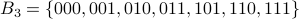 . We write the function
. We write the function 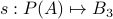 by using the mapping from every element of the power set
by using the mapping from every element of the power set
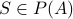 and every element of
and every element of 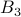 .
.
The table below shows the elements of the power set and the corresponding
value of 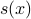 .
.
Power set elt. (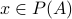 ) ) | s(x) |
| {} | 000 |
| {a} | 100 |
| {b} | 010 |
| {c} | 001 |
| {a,b} | 110 |
| {a,c} | 101 |
| {b,c} | 011 |
| {a,b,c} | 111 |
Example-4: Mathematical functions
You may have seen many examples of functions from your mathematics classes, thus far.
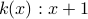 , a function from
, a function from  takes an input natural number and yields an output natural number.
takes an input natural number and yields an output natural number. is a function from
is a function from 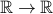 , takes an input real number and yields a real number output.
, takes an input real number and yields a real number output.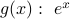 is a function from
is a function from 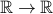 , takes an input real number and yields a real number output.
, takes an input real number and yields a real number output.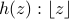 is a function from
is a function from 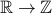 , , takes an input real number and yields an integer output.
, , takes an input real number and yields an integer output.
Non-Examples of Functions.
It remains to clarify what is not a function. In general, a mapping
from set  to set
to set  can fail to be a function for either of the
two reasons below:
can fail to be a function for either of the
two reasons below:
It leaves an element of set
 unmapped.
unmapped.It maps an element of
 to multiple elements in
to multiple elements in  .
.
If either case occurs then, the mapping fails to be a function.
Consider the two mappings shown below. The mapping on the left fails
to be a function because it does not map the elements  from the
domain, while the mapping on the right fails to be a function since
from the
domain, while the mapping on the right fails to be a function since
 is mapped to multiple elements.
is mapped to multiple elements.
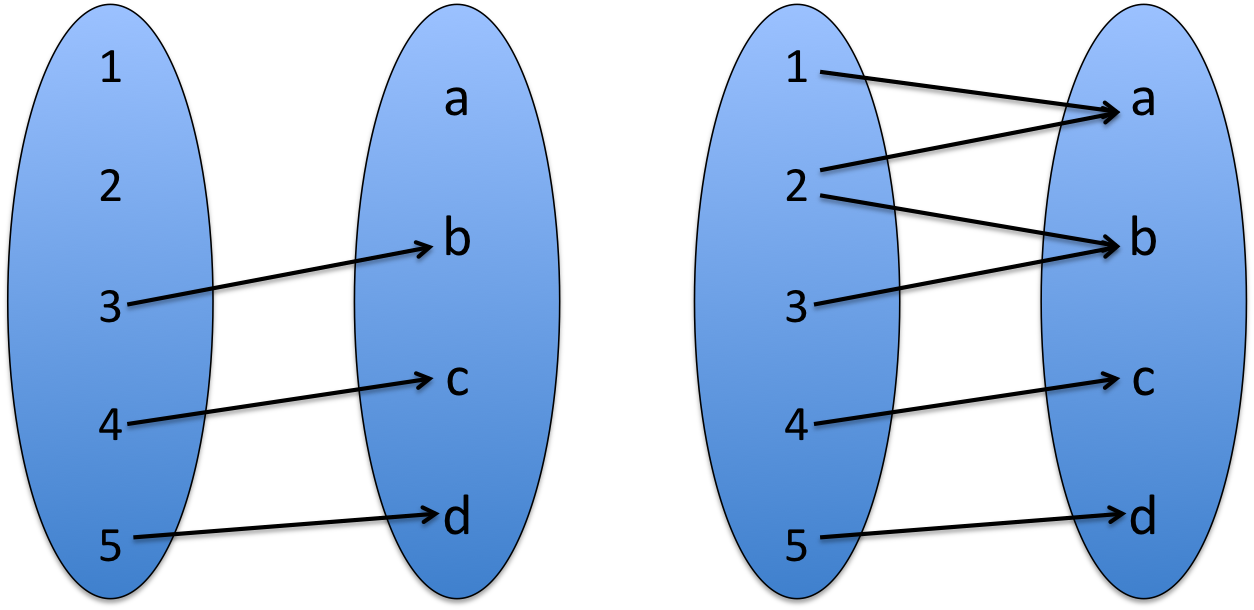 |
Mathematical non-functions
Strictly speaking, many functions that we saw in calculus are not quite functions.
The function
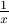 is not a function from
is not a function from 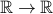 .
. It is a function however from
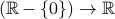 . Here, we have removed the input
. Here, we have removed the input 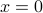 from the domain.
from the domain.
The function
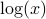 is not a function from
is not a function from 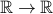 since it leaves all values
since it leaves all values 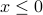 unmapped.
unmapped.If we wish to be precise, we will define the type of
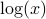 to be
to be 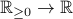 .
.
The function
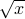 is not defined for
is not defined for 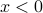 and can be defined to both positive and negative square roots when
and can be defined to both positive and negative square roots when 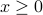 . For instance
. For instance 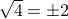 .
.If we wish to be precise, we define
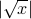 to be a function from
to be a function from 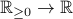 , with the domain restricted to non-negative reals.
, with the domain restricted to non-negative reals.
Relations
Formally, a relation 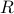 between sets
between sets  and
and  is defined as a subset of
is defined as a subset of 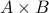 , i.e,
, i.e,  .
.
Example-1
Let us take 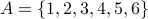 and
and  . Consider the relation
. Consider the relation  by
by
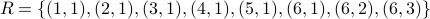
Like functions, we may view the relation as a mapping. However, unlike functions, it is possible that
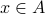 is not related to any element in
is not related to any element in  .
. 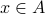 could be related to multiple elements in
could be related to multiple elements in  .
.
The relation 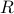 is visualized below:
is visualized below:
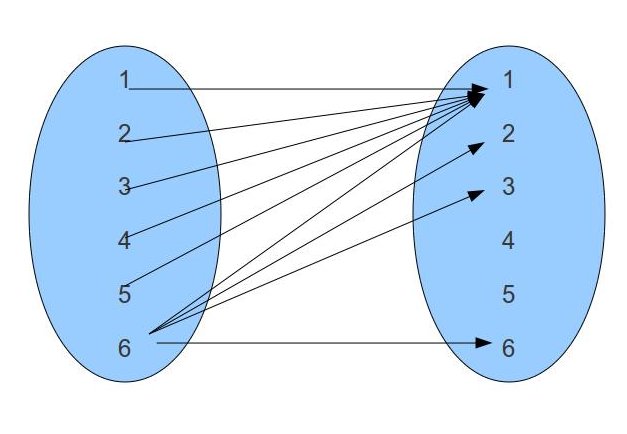 |
Functions are a special case of relations, wherein
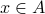 is mapped to exactly one element in
is mapped to exactly one element in  .
.
Example-2
Here is another example of a relation over numbers: 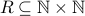 defined as
defined as
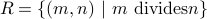
Write down some examples of elements of 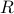 .
.
Example-3
Consider sets 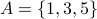 and
and 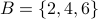 write the function
write the function 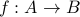 defined by
defined by 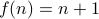 as a relation
as a relation
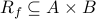 .
.
Counting Relations
If  is a set with
is a set with 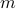 elements and
elements and  with
with  elements then how many relations can exist between
elements then how many relations can exist between  and
and  ? How many functions?
? How many functions?
Answer in class.
Domains/Co-Domains
Let 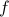 be a function
be a function 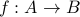 . We say that
. We say that  is the domain of
is the domain of 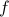 and
and  is the co-domain.
is the co-domain.
Similarly, let  be a relation. We say that
be a relation. We say that  is the domain of the relation and
is the domain of the relation and
 is the co-domain.
is the co-domain.
Relations On a Set
A relation 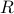 from set A to itself is called a relation on A . We can represent relations from a set to itself by a special
diagram called a graph.
from set A to itself is called a relation on A . We can represent relations from a set to itself by a special
diagram called a graph.
E.g., Let 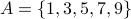 . Consider a relation
. Consider a relation  .
.
The relation has the tuples  .
The graph looks as follows:
.
The graph looks as follows:
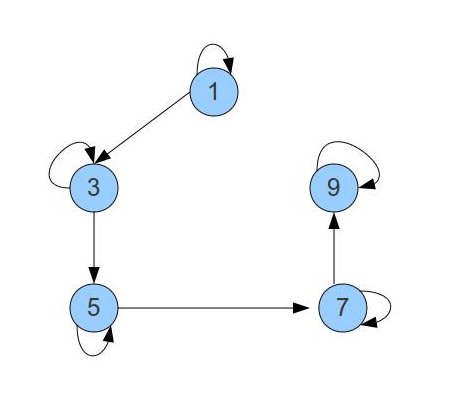 |
The rule is we have nodes or vertices for each element in the set  . If
. If 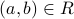 , we draw an arrow from
, we draw an arrow from  to
to 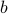 .
Graphs are very useful as visualizations of relations. We will spend 2-3 weeks at the end of this course talking about
properties of graphs.
.
Graphs are very useful as visualizations of relations. We will spend 2-3 weeks at the end of this course talking about
properties of graphs.