Sets: basic definition and operations
We will cover the topics:
Defining Sets
Operations: Union, intersections, complement, set difference.
Venn Diagrams
Cardinality: Inclusion-Exclusion Principle
Defining Sets
For now, it is convenient to assume that there is a universe  of
elements.
of
elements.
A set is any collection of elements from a universe  .
.
The concept of a set is so basic in mathematics that it defies an easy definition. Most definitions just devolve to a set is a set :-).
The contents of a set are called its elements. For an element  ,
we say
,
we say 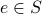 if
if  belongs to the set
belongs to the set 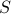 . The negation is
written as
. The negation is
written as 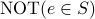 or often as
or often as 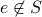 .
.
There are two ways to define a set:
Explicitly: Just list out its elements. Eg.,
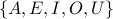 .
. Implicitly: Write a description of what belongs to the set in English or better still in Logic. Eg.,
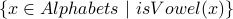 .
.
For now, whenever we are discussing sets, the universe  needs to be made clear.
needs to be made clear.
Naive Set Theory
The notion of set theory that we are studying in this lecture is called naive set theory.
The reason, we call it naive is the assumption of the universal set
 . Before the 20th century, mathematicians and philosophers imagined
a collection
. Before the 20th century, mathematicians and philosophers imagined
a collection  of all possible entities and called it the
universal set. This set
of all possible entities and called it the
universal set. This set  has literally everything one can
imagine: goats, ants, Higgs Bosons, tables, chairs,
numbers, groups and all that. Think of it, and presto!, the
universal set
has literally everything one can
imagine: goats, ants, Higgs Bosons, tables, chairs,
numbers, groups and all that. Think of it, and presto!, the
universal set 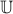 has it. But the work of mathematicians such
as Cantor and Bertrand Russell in the early 20th century proved that
the universal set
has it. But the work of mathematicians such
as Cantor and Bertrand Russell in the early 20th century proved that
the universal set 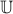 cannot exist, since it existence leads
to paradoxes or contradictions.
cannot exist, since it existence leads
to paradoxes or contradictions.
The universal set 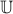 containing everything does not exist.
containing everything does not exist.
Therefore, we will continue to describe a version in this notes that we will call informally ‘‘semi-naive’’ (Note that this is our own invention and not a standard term in mathematics). Wherever possible, we will note the changes needed due to the non-existence of an universal set.
Example 1: Integers
We assume that the universe is restricted the set of all integers 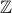 .
.
What do the following sets define:
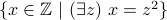 .
. All numbers that are perfect squares.
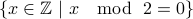
All even numbers.
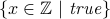 .
. All numbers in
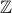 , since every number trivially satisfies the predicate
, since every number trivially satisfies the predicate 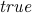 .
.
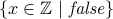 .
. The empty set: since no number satisfies the predicate
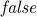 .
.
Note that restricting our universe to the set of integers, poses no contradiction or paradox in the definitions above.
Example 2: Animals
Let the universe  be all the animal species on planet earth.
be all the animal species on planet earth.
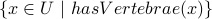 defines all animals with vertebrae.
defines all animals with vertebrae. 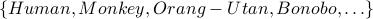 describes all primates. Note the loose usage of
describes all primates. Note the loose usage of  to signify and so on.
to signify and so on.
Note that restricting the universe to that of all animal species on the planet earth makes the sets above well defined and free of contradictions.
Empty/Universal Sets
The set with no elements is called the empty set. It is written 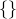 or
or 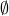 . We will use the latter.
. We will use the latter.
Naive set theory often adds a special universal set 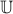 . As
noted earlier, the universal set does not exist, and will need to be
unlearned.
. As
noted earlier, the universal set does not exist, and will need to be
unlearned.
However, in many contexts, we will specifically name a set such as
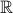 (the set of all real numbers) to be a restricted
universe. Since
(the set of all real numbers) to be a restricted
universe. Since 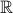 is a well-defined set, it is fine to
assume such a set as a restricted universe.
is a well-defined set, it is fine to
assume such a set as a restricted universe.
Union, Intersection, Difference and Complement.
Let 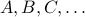 denote sets drawn from a restricted universe
denote sets drawn from a restricted universe  .
.
Union:
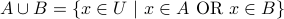 .
. Intersection:
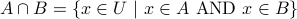 .
. Set Difference:
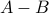 (also written
(also written 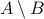 )
) 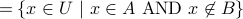 .
.
The operation of complementation is defined in naive set theory.
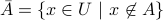 .
.
If we operate inside a restricted universe  , then
, then 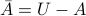 .
.
Otherwise, 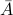 does not exist, strictly speaking, because the
universal set
does not exist, strictly speaking, because the
universal set 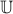 containing everything does not exist.
containing everything does not exist.
Example 1
Let  be the restricted universe given by set of all integers
be the restricted universe given by set of all integers 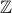 .
.
Let 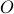 be the set of all odd integers,
be the set of all odd integers, 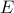 be the set of all even integers,
be the set of all even integers,
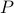 be the set of all prime integers and
be the set of all prime integers and 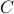 be the set of all composite numbers (
be the set of all composite numbers (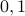 are neither prime nor composite).
are neither prime nor composite).
What are the sets?
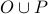
The set of numbers that are either odd or prime. We can write it as
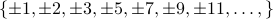 (caution on using
(caution on using  ).
).
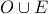
The set of all integers.
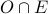
The empty set.
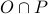
The set of all odd and prime numbers.
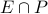
The set
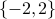 (we assume -2 is prime as well).
(we assume -2 is prime as well).
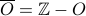
The complement of the odd numbers is the set of even numbers.
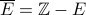
The complement of the even numbers is the set of odd numbers.
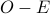
The set of all odd numbers since “subtracting” even numbers from odd, ends up removing nothing from the set.
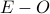
The set of all even numbers since “subtracting” odd numbers ends up removing nothing from the set.
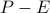
The set of all odd prime numbers.
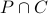
Empty set.
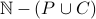
The set
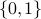 of neither prime nor composite numbers.
of neither prime nor composite numbers.
Example-2
Is 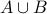 the same as
the same as 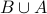 ? What about
? What about  ?
?
In general,
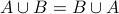 but
but 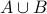 is not
necessarily the same as
is not
necessarily the same as  . As an example take
. As an example take 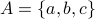 and
and 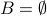 . We have
. We have 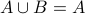 but
but 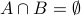 .
.
Is 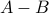 the same as
the same as 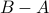 ? Give a simple example.
? Give a simple example.
Not necessarily, Take
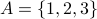 and
and 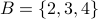 . We have
. We have
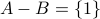 and
and 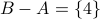 .
.
Finite Vs. Infinite Sets
Finite sets are those that have finitely many elements. Infinite sets, on the other hand, have infinitely many elements. We will define infinite sets and deal with infinite sets in a lot of detail soon.
Venn Diagrams
Venn Diagrams are easy diagrammatic ways of visualizing sets and operations between them. We assume that you already know a lot about these (this is high school material, really). We will do some quick recap in class.
On the other hand, Venn diagrams are nothing to sneeze at. The wikipedia article on Venn diagrams or this site has a lot of interesting information.
We can use Venn diagrams to prove certain properties of sets.
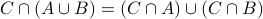 . (Distributivity Law #1)
. (Distributivity Law #1) 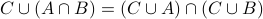 . (Distributivity Law #2)
. (Distributivity Law #2) 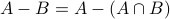 .
.
Cardinality
The cardinality of a set is the number of elements in it. For now, it makes sense to talk of cardinality just for finite sets. We will discuss the issue of infinite sets and cardinality after we have covered relations and functions. The cardinality of the empty set is, of course, zero. The cardinality of a set can never be negative.
What is the cardinality of the following sets:
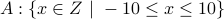 (Answer: 21).
(Answer: 21). 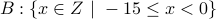 (Answer 15).
(Answer 15). 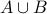 (Answer: 26)
(Answer: 26)  ? (Answer: 10)
? (Answer: 10) 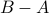 ?
? 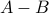 ?
?
The cardinality of a set  is denoted
is denoted 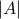 or sometimes by
or sometimes by
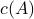 . We will use
. We will use 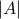 .
.
Notice the following interesting fact: 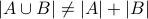 . Why is this true?
. Why is this true?
Using a Venn diagram, we can derive that
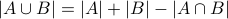
The relation above is called the inclusion exclusion principle.
We can extend it to three sets 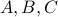 :
:
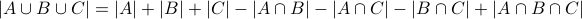
Notice the curious sign change!!
Example-1
Let 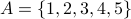 and
and 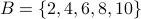 .
.
Verify the inclusion-exclusion principle for 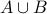 ?
?
We see that 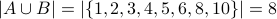 .
.
We can also see this using the inclusion exclusion principle:
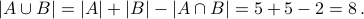
Example-2
If we look at all numbers from  to
to  . How many numbers contain a
. How many numbers contain a  ?
?
Off the top of our head, this kind of calculation is tricky. We have 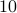 numbers with
numbers with
 in the second digit (
in the second digit (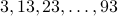 ) and
) and 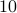 numbers with a
numbers with a  in the first digit
in the first digit
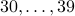 . Therefore, there are total of
. Therefore, there are total of 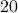 numbers with a
numbers with a  in them. However, note
that
in them. However, note
that 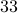 has been counted twice. So the answer should be
has been counted twice. So the answer should be 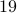 .
.
Using inclusion-exclusion: Let  be the set of all numbers with
be the set of all numbers with  in the seond digit
and
in the seond digit
and 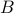 be all numbers with
be all numbers with  in the first (most-significant) digit. Our argument above
is using the inclusion exclusion principle:
in the first (most-significant) digit. Our argument above
is using the inclusion exclusion principle:
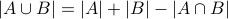
Example -3
How many numbers between  and
and 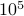 are divisible by
are divisible by 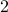 or by
or by  or by
or by 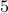 ?
?
Let us fix the universe to be 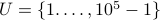 .
.
Let 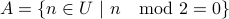 . Similarly, let
. Similarly, let 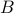 be the numbers divisible by
be the numbers divisible by  and
and
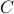 be the numbers divisible by
be the numbers divisible by 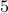 .
.
We seek 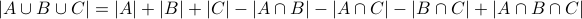 .
.
We have
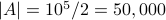 .
. 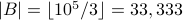 .
. 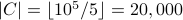 .
. 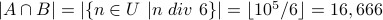
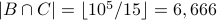
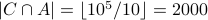 .
. 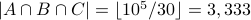 .
.
Overall 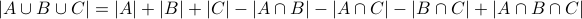 =
= 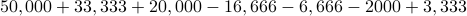 =
=
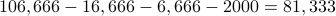 .
.
(I could be off in my calculations, please check).
General Inclusion Exclusion Principle
We have seen inclusion exclusion for cardinality of 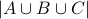 . Suppose we have
. Suppose we have 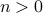 sets
sets 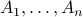 , we can generalize this to
, we can generalize this to
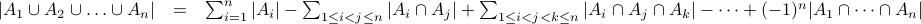
Puzzle (Counting Prime Numbers)
Given a list of prime numbers from  to
to 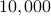 , show how the list can be used to count the number of primes from
, show how the list can be used to count the number of primes from  to
to 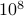 using
inclusion exclusion.
using
inclusion exclusion.
Let us try a simpler case of counting primes from 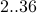 . Instead of primes, we will count composites. Once we count composites, we can immediately
conclude how many primes there are.
. Instead of primes, we will count composites. Once we count composites, we can immediately
conclude how many primes there are.
The universal set is 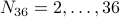 . Let us define the set
. Let us define the set 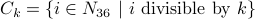 . We omit
. We omit  since it is neither prime nor composite.
since it is neither prime nor composite.
We take our seed set of prime numbers to be 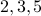 .
.
Theorem Every composite number from 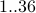 is divisible by
is divisible by 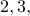 or
or 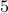 . In other words, every composite number
. In other words, every composite number 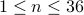 has
has 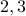 or
or 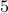 as one of their prime factor.
as one of their prime factor.
Proof is by contradiction. Let  be a composite number such that
be a composite number such that 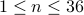 and
and  does not have
does not have 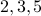 as a prime
factor. Therefore,
as a prime
factor. Therefore,  can be factored as a product of
can be factored as a product of 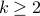 prime numbers
prime numbers 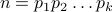 , wherein,
, wherein, 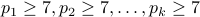 . In other words, we conclude that
. In other words, we conclude that 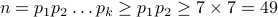 . But we assumed that
. But we assumed that 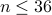 , yielding a contradiction.
, yielding a contradiction.
In other words, we will first count 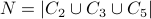 using the inclusion exclusion principle. This will give us the count of composites with a caveat.
using the inclusion exclusion principle. This will give us the count of composites with a caveat. 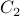 includes
includes 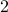 ,
,
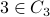 and
and 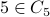 . So whatever the cardinality of their union is, we need to subtract
. So whatever the cardinality of their union is, we need to subtract  from them to obtain numbers that are truly composite.
from them to obtain numbers that are truly composite.
We write
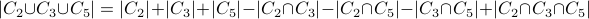
We note that 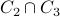 is just
is just 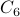 . We know
. We know 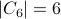 because there are
because there are 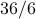 numbers that are divisible by
numbers that are divisible by 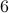 .
.
Therefore,
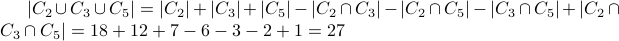
The number of composites is therefore 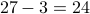 (why did we subtract
(why did we subtract  ?)
The number of primes will be
?)
The number of primes will be 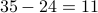 (why from
(why from 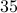 ? why not
? why not 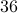 here?).
Check that there are indeed
here?).
Check that there are indeed  primes from
primes from  to
to 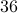 :
: 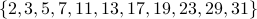 .
.
The same calculation can be carried out for all primes upto 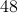 . For that we get:
. For that we get:
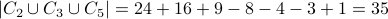
Using this, number of composites is 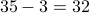 . Therefore, we conclude that
. Therefore, we conclude that 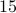 primes exist.
The additional four primes beyond
primes exist.
The additional four primes beyond 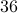 are
are 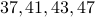 .
.
There is a very close connection between this way of counting and Eratosthenes Sieve for enumerating all primes. Therefore, inclusion-exclusion principle is often called the sieve principle.
As a fun exercise: implement a counter to solve the puzzle. You will definitely need to write a program rather than attempt this by hand.
Cartesian Products and Power Sets
We will now look at two other operations over sets:
Cartesian Products
Power Sets
Cartesian Product
Take sets  and
and 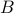 over some universe
over some universe  . The Cartesian product of
. The Cartesian product of 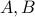 is defined as
is defined as
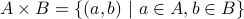
In other words, we build the set of all 2-tuples 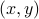 where the first component is from set
where the first component is from set  and
second component is from set
and
second component is from set 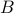 .
.
We can extend Cartesian product to more than 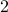 sets:
sets:
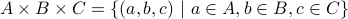
Here we take Cartesian product of  sets and the resulting product is a set of 3-tuples.
sets and the resulting product is a set of 3-tuples.
Example-1
If 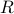 is the set of all real numbers represented by the real line, what is the set
is the set of all real numbers represented by the real line, what is the set 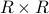 ?
?
Answer: 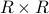 consists of all tuples of reals of the form
consists of all tuples of reals of the form 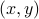 where
where 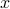 and
and 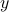 are reals.
In other words, we have moved from a single number to
are reals.
In other words, we have moved from a single number to 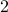 -dimensional co-ordinates.
-dimensional co-ordinates.
For simplicity, the product of a set with itself 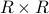 is written
is written 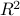 .
.
What is 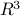 ?
?
Example-2: Empty Set
What is the Cartesian product of the empty set 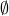 with a set
with a set  ?
?
Answer: The empty set.
Cardinality of Cartesian Products
The rule for Cartesian product is that
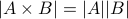
We can convince ourselves by drawing a table of all entries. Let us assume 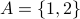 and
and 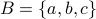 .
.
| a | b | c | |
| 1 | (1,a) | (1,b) | (1,c) |
| 2 | (2,a) | (2,b) | (2,c) |
Order of Cartesian Product Matters
If 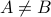 for sets
for sets 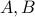 , we note that
, we note that 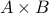 will not equal
will not equal 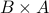 . In other words, it matters in a tuple
. In other words, it matters in a tuple 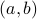 that
that  comes first and
comes first and
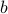 comes second. For example, if I asked you to draw a pixel at
comes second. For example, if I asked you to draw a pixel at 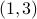 it is not the same as drawing one at
it is not the same as drawing one at  , right?
, right?
If 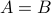 , however, it is trivial that
, however, it is trivial that 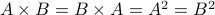 are all the same thing.
are all the same thing.
Example
What is the size of cartesian product 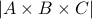 if
if 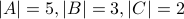 ?
?
Subset
Set  is a subset of
is a subset of 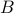 written
written 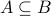 iff every element of
iff every element of  is also an element of
is also an element of 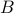 .
.
Examples
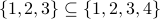 ?
? 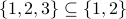 ?
? Is it true that
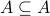 for any set
for any set  ?
? Is it true that
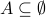 for all sets
for all sets  ?
? Is it true that
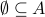 for all sets
for all sets  ?
?
Answers: yes, no, yes, no, yes!