Concepts you should know before the final (CSCI 2824, Spring 2015)
Logic (Chapter 1)
Propositional logic (Sect 1.3)
A proposition is a statement that has a truth value (which is either true or false).
Logical operators
AND (
 )
)OR (
 )
)negation (
 )
)
Logical equivalence of two propositions:
two propositions
 and
and  are logically equivalent if
they have the same truth values.
are logically equivalent if
they have the same truth values.we denote the logical equivalence of
 and
and  by
by 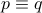
Truth table
Predicate logic (Sect 1.4)
predicates
a predicate is a statement that incorporates a variable
e.g.
 is a predicate
is a predicate
set membership
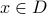 means “
means “ in
in  ”
”
quantifiers
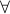 means “for all”;
e.g.
means “for all”;
e.g. 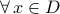 means “for all
means “for all  in
in  ”
”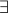 means “there exists”;
e.g.
means “there exists”;
e.g.  means “for some
means “for some  in
in  ”
”we can get a quantified statement by combining quantifiers and predicates: e.g.

negating a quantified statement (Proposition 1, Page 45):
e.g.

e.g.
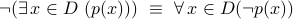
Implications (Sect 1.5)

 is called the hypothesis/premise/assumption
is called the hypothesis/premise/assumption is called the consequence
is called the consequence means “if the premise
means “if the premise  is true, then the consequence
is true, then the consequence  must be true too” (or “
must be true too” (or “ implies
implies  ”)
”)
 means +
means +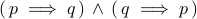 .
.“
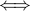 ” reads if and only if.
” reads if and only if.On paper we also write iff in short.
The proposition
 is true if and only if either
one (or both) of the following is true:
is true if and only if either
one (or both) of the following is true: is false (i.e., the premise does not hold)
is false (i.e., the premise does not hold) is true (i.e., the consequence always holds)
is true (i.e., the consequence always holds)
Hence
 is logically equivalent to
is logically equivalent to 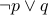
negating an implication
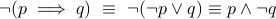
in other words, an implication is false if and only if the hypothesis holds true but the consequence is false.
contrapositive of
 is
is 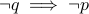
an implication is always logically equivalent to its contrapositive
the contrapositive of
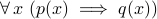 is
is 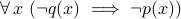 .
.the contrapositive of
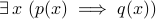 is
is 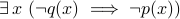 .
.
converse of
 is +
is +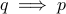
even if an implication is true, its converse may be false
e.g. the converse of “if
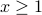 , then
, then 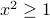 ” (which is a true statement) is
“if
” (which is a true statement) is
“if 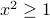 , then
, then  ” (which is a false statement).
” (which is a false statement).the converse of
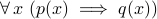 is
is 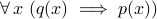 .
.the contrapositive of
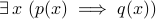 is
is 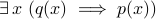 .
.
inverse of
 is
is 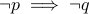
the inverse of an implication is formed by taking the contrapositive of the converse.
given an implication, its inverse and the converse are always logically equivalent.
the inverse of
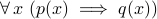 is
is  .
.the inverse of
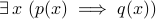 is
is 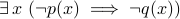 .
.
Proof techniques (Chapter 2)
Direct proofs (Sect 2.1)
Proof by contrapositive (Sect 2.1)
Proof by cases (Sect 2.2)
Proof by contradiction (Sect 2.4)
Weak induction (Sect 2.3-2.4)
Here is how we prove a statement of the form
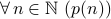 .
.Step 1: prove the base case, i.e., show that
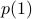 is true.
is true.Beware!! the index for the base case is the smallest index for which the statement-to-be-proved is supposed to hold. (Not necessarily the first index of the recurrence.)
Step 2: state the induction hypothesis:
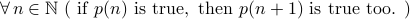
Step 3: prove the above statement.
Start with “Fix any
 and suppose that
and suppose that
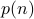 is true.”
is true.”Then show that
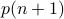 is true, usually use the recurrence
relation and the assumption that
is true, usually use the recurrence
relation and the assumption that 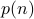 holds.
holds.
Strong induction (Sect 2.4)
Here is how we prove a statement of the form
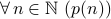 concerning recursive sequences of the form
concerning recursive sequences of the form 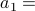 (some number),
(some number), 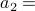 (some number),
(some number), 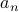 defined
in terms of
defined
in terms of 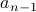 and
and 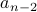 .
.Step 1: prove the base cases.
Show that
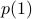 and
and 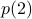 are true.
are true.
Step 2: state the induction hypothesis:
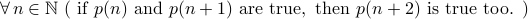
Step 3: prove the above statement.
Side topics
Division theorem (Theorem 8, Page 103)
Pigeonhole principle (Theorem 8, Page 143)
Set theory (Chapter 3)
A set is a collection of “objects”.
These objects in the set are formally called elements.
There are three common ways to describe a set:
explicit listing: all elements are listed.
E.g.
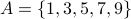
form description
E.g.
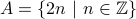
property description
E.g.
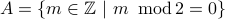 .
.
We always use curly brackets to contain the elements.
Elements in a set are unordered and nonrepeating.
Some common sets that we use:
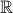 : the set of real numbers
: the set of real numbers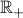 : the set of nonnegative real numbers
: the set of nonnegative real numbers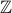 : the set of integers
: the set of integers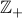 : the set of nonnegative integers
: the set of nonnegative integers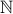 : the set of natural numbers
: the set of natural numbersfor real numbers
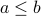 :
:![[a,b]triangleq{tinmathbb{R} | aleq tleq b}](eqs/2979912588678669817-130.png) ;
;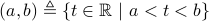 ;
;![(a,b]triangleq{tinmathbb{R} | a< tleq b}](eqs/5351240216500325787-130.png) ;
;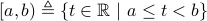 .
.
Basic notation (Sect 3.1)
For any set
 ,
, 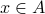 means
means  is an element of
is an element of  ;
;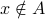 means
means  is not an element of
is not an element of  .
.
For any sets
 and
and  ,
, 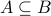 means
means  is a subset of
is a subset of  , meaning
, meaning
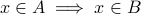
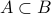 means
means  is a proper subset of
is a proper subset of  , meaning
+
, meaning
+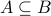 and
and 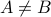 .
.
The empty set is a set that has no elements, and is denoted by
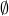 .
.
Set operations (Sect 3.1 and 3.2)
Let 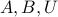 be sets and suppose that
be sets and suppose that 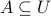 ,
, 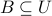 . Here we assume
. Here we assume  to be the universal set (which simply
means that everything happens inside
to be the universal set (which simply
means that everything happens inside  ).
).
 (which reads
(which reads  union
union  ) is defined as the set
) is defined as the set
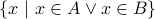 .
. (which reads
(which reads  interset
interset  ) is defined as the set
) is defined as the set
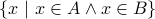 .
.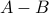 or
or 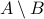 is defined as the set
is defined as the set
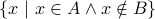 .
.The complement of
 (with respect to the universal set
(with respect to the universal set  ) is defined as
) is defined as 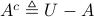 .
.The Cartesian product of
 and
and  is defined as the set of
all 2-tuples (i.e., ordered lists of length 2) with the first
component from
is defined as the set of
all 2-tuples (i.e., ordered lists of length 2) with the first
component from  and the second one from
and the second one from  . The notation is
. The notation is
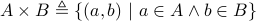 .
.We use
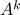 to denote
to denote  (
(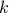 copies
of
copies
of  here), which contains
here), which contains 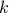 -tuples (i.e., ordered lists of
length
-tuples (i.e., ordered lists of
length 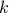 ) with all components from
) with all components from  .
.The power set of
 is the set of all subsets of
is the set of all subsets of  , and is denoted by either
, and is denoted by either 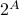 or
or 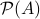 .
. A partiton of
 is a set of disjoint subsets of
is a set of disjoint subsets of  such that
their union is
such that
their union is  .
.
Cardinality and inclusion-exclusion principle (Sect 3.1 and 3.2)
Let  and
and  be sets.
be sets.
If
 has finitely many elements, we say that
has finitely many elements, we say that  is a finite
set; otherwise we say that
is a finite
set; otherwise we say that  is an infinite set.
is an infinite set.Suppose that
 is a finite set.
is a finite set.The cardinality of
 is defined as the number of elements
of
is defined as the number of elements
of  , and this number is denoted by
, and this number is denoted by 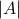 .
.Then
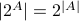 .
.
Suppose that
 and
and  are finite sets.
are finite sets.Inclusion-Exclusion principle:
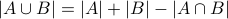 .
.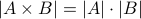 .
.
Relations and functions (Chapter 4)
Relations (Sect 4.1, 4.4, 4.5)
A relation from
 to
to  is a subset of
is a subset of 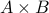 .
.A relation over
 is a subset
is a subset 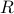 of
of 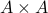 .
.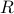 is said to be symmetric if
is said to be symmetric if 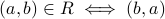 .
.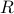 is said to be reflexive if
is said to be reflexive if 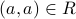 for all
for all 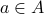 .
.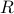 is said to be transitive if
is said to be transitive if 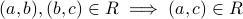 .
.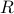 is said to be an equivalence relation if
is said to be an equivalence relation if 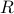 is
symmetric, reflexive and transitive.
is
symmetric, reflexive and transitive.
Functions
A function from
 to
to  is a relation
is a relation  from
from  to
to  such that:
such that:for every
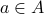 , there is exactly one bin B
, there is exactly one bin B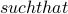 (a,b)in F$.
(a,b)in F$.we usually use the arrow notations for describing a function.
e.g.
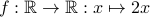 .
.
Common functions
ceiling function
 , rounding a real number up
, rounding a real number upfloor function
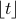 , rounding a real number down
, rounding a real number downmin/max functions
log functions
exponential functions
Injectiveness, surjectiveness and bijectiveness (Sect 4.1, 4.2)
A function
 is injective (or one-to-one) iff
is injective (or one-to-one) iff
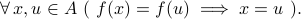
A function
 is surjective (or onto) iff
is surjective (or onto) iff
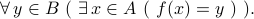
A function is bijective (or said to be a /one-to-one correspondence) iff it is both injective and surjective.
A function
 has an inverse iff
has an inverse iff 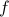 is bijective.
is bijective.In this case, we can define the inverse function of
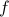 , which is denoted by
, which is denoted by 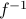 .
. E.g. Let
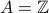 and
and 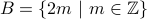 .
The function
.
The function 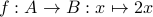 is bijective,
Its inverse is
is bijective,
Its inverse is 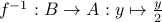 .
.
Image and preimage
Given a function
 , sets
, sets  and
and 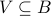 ,
,the preimage of
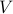 under
under 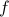 is the set
is the set
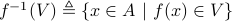 ;
;the image of
 under
under 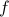 is the set
is the set
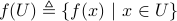 .
.
Relations between functions and set cardinality (Sect 4.3)
Given any two nonempty finite sets  and
and  ,
,
if there exists an injective function from
 to
to  , then
, then 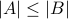 ;
;if there exists a surjective function from
 to
to  , then
, then 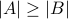 ;
;if there exists a bijective function from
 to
to  , then
, then  .
.
Growth of functions (Sect 4.8)
Given any two functions 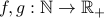 ,
,
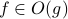 iff there exists positive numbers
iff there exists positive numbers
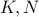 such that
such that 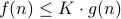 for all
for all 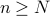 ;
;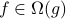 iff there exists positive numbers
iff there exists positive numbers
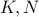 such that
such that 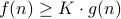 for all
for all 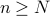 ;
;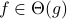 iff
iff 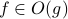 and
and 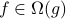 ;
;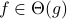 iff
iff 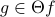 .
.
A few important results:
For any polynomial
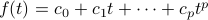 with
with
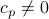 ,
, 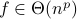 .
. Let
 .
Then
.
Then 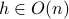 and
and  .
.
Please remember to review the master theorem. (See Theorem 9 in Section 4.8, Page 358.)
Basic combinatorics (Chapter 5)
Four basic structures
ordered lists (repetitions allowed, ordering matters)
unordered lists (repetitions allowed, ordering does not matters)
permutations (repetitions not allowed, ordering matters)
combinations (repetitions not allowed, ordering does not matter)
Counting lists
Please check the online lecture notes and the examples in the textbook (if you have it).
Permutations
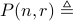 number of permutations of
number of permutations of  numbers from
numbers from 
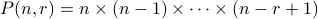 .
.
Combinations
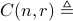 number of subsets of
number of subsets of  that
are of size
that
are of size 
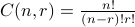
Solving recurrence
you should be able to solve recurrences of the form
e.g.
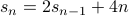 via repeated substitution;
via repeated substitution;e.g.
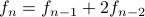 by solving the associated quadratic equation
by solving the associated quadratic equation 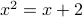 .
.
Probability (Chapter 6)
Suppose we have an experiment where there are only finitely many possible outcomes.
The sample space
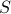 is the set of all possible outcomes.
is the set of all possible outcomes.An event
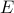 is a subset of the sample space.
is a subset of the sample space.The probability of an event
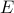 is the ratio
is the ratio 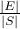 .
.
Mutually exclusive events; independent events; conditional probability
Let  and
and  be two events from an experiment.
be two events from an experiment.
 and
and  are mutually exclusive if
are mutually exclusive if  .
. In practices this simply means the two events cannot happen at the same time.
If
 and
and  are mutually exclusive, then
are mutually exclusive, then 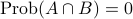
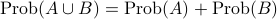 .
.
The probability of
 given
given  is defined by the fraction
is defined by the fraction
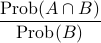 .
. and
and  are said to be independent if
are said to be independent if 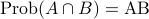 .
.In practice this means that whether
 happens or not does not depend on whether
happens or not does not depend on whether  happens or not.
happens or not.
Expected value
Given an experiment with sample space  ,
,
A random variable is a function that maps each outcome to a real number. In other words, every function
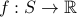 is a random variable.
is a random variable.The expected value of a random variable
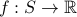 is
is
![mathbb{E}[f] = sum_{sin S} f(s)cdot mathrm{Prob}({s})](eqs/6912879784213219633-130.png) .
.
Bernoulli trials
A Bernoulli trial is an experiment that has only two outcomes (which we usually call “success” and “failure”).
Suppose that
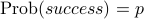 .
(Then
.
(Then 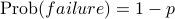 .)
.)If a Bernoulli trial is repeated
 times, the probability that
there are exactly
times, the probability that
there are exactly 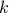 successes is
successes is 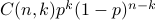 .
.If the average payoff of one Bernoulli trial is
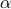 ,
then the average payoff of
,
then the average payoff of  Bernoulli trial is
Bernoulli trial is 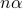 .
.
Graph theory (Chapter 7)
You will need to know what the following terms mean regarding directed and undirected graphs :
degrees; in-degree; out-degree; source; sink
walks (or paths in undirected graphs)
directed cycles (or cycles in undirected graphs)
Eulerian graphs
bipartite graphs
trees and leaves
strongly connected components of digraphs (or connected components of undirected graphs)