Sequences: Examples (CSCI 2824, Spring 2015)
In the following we consider some examples on sequences and summations.
We would be just guessing closed form/summation expressions in the following examples. We will learn in Chapter 2 how to prove that a guess is correct.
Examples on sequences
Example 1: finding a simple formula
Example 2: compound interest
Example on summation
Example 1: using summation notation
Example 2: Ex 24(a) from textbook Sect 1.2
Example 3: bubble sort — worst case complexity
Examples on Sequences
Example 1: finding a simple formula
How do we find a simple formula that gives the terms of a sequence that begins with the following list?
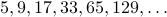
It is not too difficult to notice that
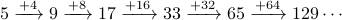
We look at two different expression: the recursive relation and the closed form expression.
Method 1: using recursive relation
A simpler way in this example is to use recursive relation.
Step 1: define the initial term. (A recursion always starts with some initial term(s)!)
Step 2: (optional, i.e., if the sequence is too difficult) assign indices to each term in the sequence by drawing a table:
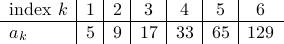
Step 3: identify the pattern — how
does the next term depend on the previous one?
For example, we see that the increment is always some power of 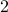 :
:
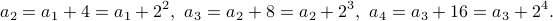
After writing out a few terms, we can guess a formula! In this case, the recursive relation would be
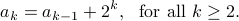
Therefore the final answer is:
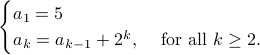
It is very important to define the initial term if you choose to
use recursive relation! Otherwise the recursive relation
would not be well-defined — if I don't know what 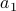 is,
how would I know what
is,
how would I know what 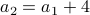 is, right?
is, right?
Method 2: closed form expression
Using the recursive relation, you could actually obtain a closed form expression by substitution.
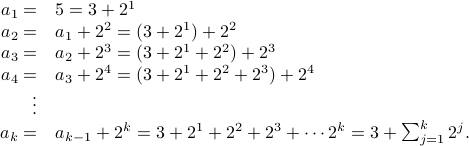
Hence the final answer is:
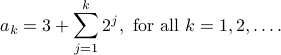
Note that for closed form expression, we do not need to specify the initial case, since each term is expressed directly in terms of the index and the expression is independent of the previous term.
Example 2: compound interest
Suppose Tom put $5000 in his savings account, which pays 5% interest once a year into his account. Assuming that Tom does not deposit or withdraw any money from the account, how much money would there be in the account 7 years after the $5000 deposit?
Step 1: figuring out the recursive relation.
Let 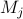 be the
amount of money in the account after
be the
amount of money in the account after 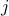 years of deposit.
Obviously,
years of deposit.
Obviously, 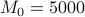 and for
and for 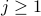 (i.e., after at least one year)
we have
(i.e., after at least one year)
we have
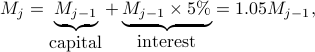
which is a recursive relation.
Step 2: using substitution to get the closed form expression. But what is the numeric amount after 7 years? This would require substitution, like this:
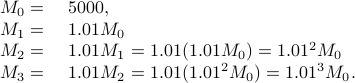
In general it looks like we have the following closed form expression:
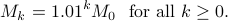
Step 3: take 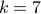 .
So a good guess of the numeric amount in the savings account
after 7 years would be
.
So a good guess of the numeric amount in the savings account
after 7 years would be
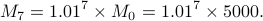
Summation
Example 1
How do we express 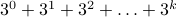 in summation notation?
in summation notation?
First we can draw a table matching the terms in the summation with appropriate indices:
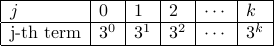
We see that the index  runs from
runs from 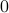 to
to 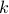 , so we know that the
answer would be in the form
, so we know that the
answer would be in the form 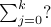 (i.e., the lower limit
is given by the first index
(i.e., the lower limit
is given by the first index 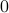 and the upper limit is given
by the last index
and the upper limit is given
by the last index 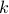 ). It remains to determine the summand, which is
easy: it is simply
). It remains to determine the summand, which is
easy: it is simply 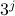 (noting how the
(noting how the 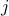 -th term depends
on the index
-th term depends
on the index 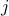 in the table). Therefore the answer is
in the table). Therefore the answer is
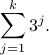
Example 2: Exercise 24(a) from Section 1.2 of textbook
How do we express the following sum using summation notation?
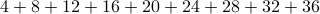
We observe that the 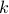 -th term in the summation is
-th term in the summation is 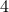 times
times 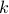 .
Alternatively, by drawing the table:
.
Alternatively, by drawing the table:
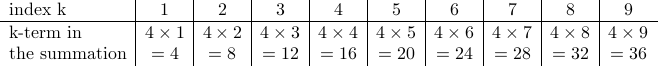
we see that the summand takes the form 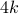 , and the lower and upper
limits are given by
, and the lower and upper
limits are given by  and
and 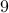 , respectively. Hence the sum equals
, respectively. Hence the sum equals
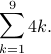
Example 3: Bubble sort
One way of algorithmically sorting a finite sequence of numbers in ascending (or descending) order is to use the (not so efficient) bubble sort algorithm. (For illustration, see the gif example from Wikipedia page on bubble sort.) A pseudocode of the bubble sort algorithm is as follows:
INPUT: a(1),...,a(n) for (i=1; i<=n; i++){ for(j=1; j<i, j++){ if(a(j)>a(j+1)){ swap a(j) and a(j+1); } } } OUTPUT: a(1),...,a(n) sorted in ascending order
The nontrivial operation involved in the bubble sort is
comparing two numbers (i.e., checking the ‘‘if’’ condition
in the inner for-loop). How many comparisons need to be done
if the input finite sequence is of length  ?
?
In the bubble sort algorithm, one comparison occurs within each
iteration of the inner for-loop. Since the inner for-loop
is executed 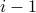 times at the
times at the 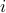 -th iteration of the outer for-loop,
and the outer for-loop is executed
-th iteration of the outer for-loop,
and the outer for-loop is executed  times,
the total number of comparison made is
times,
the total number of comparison made is
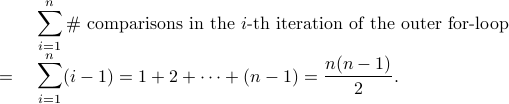
Note: In the lecture, we consider the following version of bubble sort that attempts to lower the number of comparison needed.
INPUT: a(1),...,a(n) flag=true; for (i=1; i<=n; i++){ if(flag){ for(j=1; j<i, j++){ flag=false; if(a(j)>a(j+1)){ swap a(j) and a(j+1); flag=true; } } } } OUTPUT: a(1),...,a(n) sorted in ascending order
And we asked the following question:
what is the worst-case complexity of
bubble sort in terms of number of comparisons?
That is, for any fixed length  of
input finite sequence, what is the largest possible
number of comparisons performed by the bubble sort?
of
input finite sequence, what is the largest possible
number of comparisons performed by the bubble sort?