Algorithms (CSCI 3104, Fall 2016)
In this page, we will post new challenge problems and their solutions. For each challenge problems, students are invited to send their solutions to the instructor. Note that
There is no compulsion to solve these problems and no credit is given for solving them.
Also, the instructor will be able to help you out during office hours only if there are no students with questions on the actual materials in syllabus.
Do not troll online sources asking for solutions. You are meant to solve these problems on your own or as a team of friends/classmates. Asking experts online defeats the purpose.
The best solution for each week, as judged by the instructor, will receive a small prize. For multiple, equally good solutions, lots will be drawn to determine the winner. However, people who have won in the past may be eliminated from the lottery. :-)
Fall 2016 Problems
Week 3: Find max occupancy
We are given the everyday airplane schedule at a busy international
airport serving 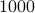 s of flights. For each airplane, we know the
landing time and takeoff time.
s of flights. For each airplane, we know the
landing time and takeoff time.
| ID | Lands (minutes after 12 midnight) | Takes off (minutes after 12 midnight) | |
| UA123 | 200 | 325 | |
| UA135 | 450 | 643 | |
| … | … | … |
Suppose we are given a large list containing pairs of landing and takeoff times for
each plane, expressed in minutes after midnight. Write an efficient algorithm
that will present the airport manager information about the number of planes in the
airport during the various time intervals of time. In particular, the table must be
sorted by increasing times, should cover the entire 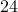 hour period and should
have as few rows as possible.
hour period and should
have as few rows as possible.
| Start time (mins after midnight) | End time | # of flights | |
| 0 | 20 | 0 | |
| 20 | 45 | 15 | |
| 45 | 60 | 12 | |
| 60 | 250 | 18 | |
| … | … | … |
Week 1: Find smallest missing positive number in an array.
You are given an array of 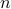 positive numbers. Eg., consider the array
positive numbers. Eg., consider the array ![[1,6,2,5,4]](eqs/6700073144737139257-130.png) .
Find the smallest positive number that is missing in the array. For the example given above,
the smallest missing number is
.
Find the smallest positive number that is missing in the array. For the example given above,
the smallest missing number is 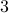 . If all elements from
. If all elements from  to
to 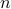 are present, then the
smallest missing number is
are present, then the
smallest missing number is  .
.
Your algorithm should run in linear time, ie 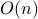 , given the size of the array
, given the size of the array 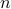 . You are not allowed to
use extra arrays or hashtables. You may however rearrange the elements in the input array.
. You are not allowed to
use extra arrays or hashtables. You may however rearrange the elements in the input array.
Successfully solved: Byron Becker and Chance Roberts
Solution
First, we can find the minimum element of the array  and subtract
this minimum element from everything. This way, elements in the array
start from
and subtract
this minimum element from everything. This way, elements in the array
start from 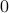 .
.
Suppose the new array has 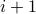 as the smallest missing elements,
we should be able to discover contiguous elements
as the smallest missing elements,
we should be able to discover contiguous elements 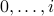 .
The algorithm we propose is going to attempt to find
.
The algorithm we propose is going to attempt to find 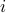 by
placing the elements
by
placing the elements  in the positions
in the positions ![a[0],ldots,a[i]](eqs/5832697745568697359-130.png) respectively.
respectively.
def findSmallestMissing(a): n = len(a) m = min(a) for i in range(0,n): a[i] = a[i] -m
To do so, the algorithm maintains two counters 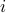 ,
, 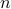 . Initially,
. Initially,
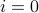 and
and 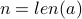 . The following invariant will be maintained,
. The following invariant will be maintained,
For the subarray ![a[0],ldots, a[i-1]](eqs/1892119995585970884-130.png) , we will place the elements
, we will place the elements
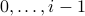 . The subarray
. The subarray ![a[n:len(a)]](eqs/842122707808496055-130.png) will contain elements that
for some reason or another cannot be the missing elements.
will contain elements that
for some reason or another cannot be the missing elements.
i = 0
n = len(a)
while (i < n):
if (a[i] == i): # a[i] already equals i, nothing more to do
i=i+1
else:
if (a[i] < i): # a[i] is strictly less than i
# This means a[i] is a repeated element and cannot be missing
swap(a,i,n-1) # Place a[i] in the range of elements that cannot be the missing one
n=n-1 # reduce n by 1
else:
e=a[i] # Let us call e = a[i]
if (e < n):
if (a[e] == e): # if a[e] already has e in it, e cannot be missing
swap(a,i,n-1)
n = n -1
else: # otherwise, place a[e] = e and bring a[i] = a[e]
e = a[i]
swap(a,i,e)
else: # if e >= n
swap(a,i,n-1) # then a[i] cannot be missing
n = n-1
Once this is done, we can search for the first element where ![a[j] != j](eqs/3047990865234757952-130.png) that is the missing
element. The overall code can be downloaded.
that is the missing
element. The overall code can be downloaded.
Let us illustrate what happens when we call ’'findSmallestMissing([0,3,2,0,4,6,7,9,1,11,13,11])’’
| i | n | a[0:i] | a[i:n] | a[n:len(a)] | |
| 0 | 12 | [] | [0, 3, 2, 0, 4, 6, 7, 9, 1, 11, 13, 11] | [] | |
| 1 | 12 | [0] | [3, 2, 0, 4, 6, 7, 9, 1, 11, 13, 11] | [] | |
| 1 | 12 | [0] | [0, 2, 3, 4, 6, 7, 9, 1, 11, 13, 11] | [] | |
| 1 | 11 | [0] | [11, 2, 3, 4, 6, 7, 9, 1, 11, 13] | [0] | |
| 1 | 10 | [0] | [13, 2, 3, 4, 6, 7, 9, 1, 11] | [11, 0] | |
| 1 | 9 | [0] | [11, 2, 3, 4, 6, 7, 9, 1] | [13, 11, 0] | |
| 1 | 8 | [0] | [1, 2, 3, 4, 6, 7, 9] | [11, 13, 11, 0] | |
| 2 | 8 | [0, 1] | [2, 3, 4, 6, 7, 9] | [11, 13, 11, 0] | |
| 3 | 8 | [0, 1, 2] | [3, 4, 6, 7, 9] | [11, 13, 11, 0] | |
| 4 | 8 | [0, 1, 2, 3] | [4, 6, 7, 9] | [11, 13, 11, 0] | |
| 5 | 8 | [0, 1, 2, 3, 4] | [6, 7, 9] | [11, 13, 11, 0] | |
| 5 | 8 | [0, 1, 2, 3, 4] | [7, 6, 9] | [11, 13, 11, 0] | |
| 5 | 8 | [0, 1, 2, 3, 4] | [9, 6, 7] | [11, 13, 11, 0] | |
| 5 | 7 | [0, 1, 2, 3, 4] | [7, 6] | [9, 11, 13, 11, 0] | |
| 5 | 6 | [0, 1, 2, 3, 4] | [6] | [7, 9, 11, 13, 11, 0] | |
| 5 | 5 | [0, 1, 2, 3, 4] | [] | [6, 7, 9, 11, 13, 11, 0] |
Here the smallest missing element is 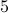 . It is found by incrementally
arranging the elements
. It is found by incrementally
arranging the elements 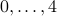 in the initial portion of the array and
pushing elements that cannot be missing to the end of the array.
in the initial portion of the array and
pushing elements that cannot be missing to the end of the array.
Why does this work in linear time?
Each step of the loop, one of the following happens:
(a) 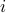 increases by
increases by  , increasing the number of contiguous elements in the start of the array.
(b)
, increasing the number of contiguous elements in the start of the array.
(b) 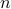 decreases by
decreases by  , increasing the number of elements that cannot be the missing elements.
(c) Or else, we take the element
, increasing the number of elements that cannot be the missing elements.
(c) Or else, we take the element ![e=a[i]](eqs/8805835494230305602-130.png) and swap it with
and swap it with ![a[e]](eqs/2835691962625600130-130.png) , provided,
, provided, ![a[e]](eqs/2835691962625600130-130.png) is not already
is not already  (in which
case (b) happens). This means, that the number of elements for which
(in which
case (b) happens). This means, that the number of elements for which ![a[j] = j](eqs/5526524312461867300-130.png) holds increases by
holds increases by  .
.
Using the three facts above, we can prove that the running time is 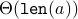 .
.