Probabilistic Models of
Human and Machine Intelligence
CSCI 5822
Assignment 7
Assigned 4/1/18
Due 4/10/18
Goal
The goal of this assignment is to explore
topic models -- to see how they are applied to data and how
model hyperparameters affect the outcome of the computation.
Before you start
Select a topic modeling package, or for
extra credit, write your own. I'm guessing that most of you will
want to use the LDA
class that is available in scikit learn. It
estimates posteriors with variational Bayes, not with Gibbs
sampling. It also has the capability for doing online training.
"Online training" means that it processes the data in small
batches, which is the only way to train if you have a really
huge data set and can't sweep through all the data at once. For
this assignment, using batch training will be fine. The
variational Bayes algorithm used for training this version of
LDA is described in this
paper. You'll need to take a look at the paper to
figure out how the notation we've discussed maps to the notation
in the scikit learn documentation.
(One big hint: the parameter we have called α has the same name
but the parameter we have called β is renamed η, and β is
confusingly used instead for the topic-conditional word
distribution.)
Here are a few additional topic modeling packages I've seen.
You can even write your own. The amount of code needed is pretty minimal to do Gibbs sampling, and all the equations are specified in my class notes or in the text. Some of the packages will have default values for parameters (α, β) and sampling procedure (# burn in iterations, # data collection iterations). Make sure you pick a package that gives you enough flexibility for the rest of the assignment; that is, you will need to estimate P(T|D) and P(W|T) from the topic assignments.
Here are a few additional topic modeling packages I've seen.
scikit learn LDA
UCI Topic modeling toolbox
Mallet (machine learning for language, Java based implementation of topic modeling)
Mahout (Java API that does topic modeling)
C implementation of topic models
windows executable of C implementation (runs from the command line)
Stanford Topic Modeling Toolkit Python implementation and documentation
R (statistics language) implementation and documentation
UCI Topic modeling toolbox
Mallet (machine learning for language, Java based implementation of topic modeling)
Mahout (Java API that does topic modeling)
C implementation of topic models
windows executable of C implementation (runs from the command line)
Stanford Topic Modeling Toolkit Python implementation and documentation
R (statistics language) implementation and documentation
You can even write your own. The amount of code needed is pretty minimal to do Gibbs sampling, and all the equations are specified in my class notes or in the text. Some of the packages will have default values for parameters (α, β) and sampling procedure (# burn in iterations, # data collection iterations). Make sure you pick a package that gives you enough flexibility for the rest of the assignment; that is, you will need to estimate P(T|D) and P(W|T) from the topic assignments.
PART I
Write code for and run a generative topic model that
produces synthetic data. For this small scale example,
generate 200 documents each with 50 word tokens from a
dictionary of 20 word types and 3 topics.
Use α=.1, β=.01.
[I am using the notation we discussed in class.]
Show a sample document. Show a sample topic distribution---a probability table over the 20 word types representing P(Word|Topic) for some topic. To use consistent notation across the class, label your words A-T (the first 20 letters of the alphabet), so that a document will be a string of 50 letters drawn from {A, ..., T}. When you generate output, make sure it is in a format that can be read by the topic modeling package you downloaded (see Part II).
Hint: Barber's BRML Toolkit includes a function for drawing from a Dirichlet: dirrnd. numpy.random.dirichlet works if you're using python. There's other code on the web as well.
Show a sample document. Show a sample topic distribution---a probability table over the 20 word types representing P(Word|Topic) for some topic. To use consistent notation across the class, label your words A-T (the first 20 letters of the alphabet), so that a document will be a string of 50 letters drawn from {A, ..., T}. When you generate output, make sure it is in a format that can be read by the topic modeling package you downloaded (see Part II).
Hint: Barber's BRML Toolkit includes a function for drawing from a Dirichlet: dirrnd. numpy.random.dirichlet works if you're using python. There's other code on the web as well.
PART II
Run your topic modelling package with T=3,
α=.1, β=.01 on your
synthetic data set. Compare the true topics (in your
generative model) to the recovered topics. The 'true
topics' are the P(Word | Topic) distributions like the one you
showed in part I. The 'recovered topics' are the estimate of
P(Word | Topic) that comes from your model. You should
decide on a sensible means of comparing the distributions.
PART III
The bias α=.1 encourages sparse topic
distributions and the bias β=.01 encourages sparse
distributions over words. Change one of these biases and find
out how robust the results are to having chosen parameters that
match the underlying generative process. You may wish to
quanitfy how changing these parameters affects the results in
terms of an entropy measure. For example, if you modify α,
then you might want to compare the mean entropy of topic
distributions:
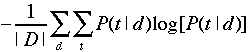
This is a measure of how focused the distribution of topics is
on average across documents. As you increase α, this entropy
should increase. If you modify β, you can evaluate
the consequence via the mean entropy of the word distribution:
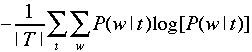
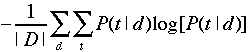
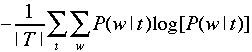
PART IV (OPTIONAL FOR EXTRA CREDIT)
Run the topic model, with parameters you
select, on a larger, interesting data set. Data sets are
abundant on the web. I only ask that it be an English
language data set so that other members of the class can see and
understand your results. The UCI Matlab Topic Modeling Toolbox
includes a variety of data
sets. There's also a corpus of 2246 articles from
the Associated
Press available from Blei at Princeton. Jim Martin has a
corpus of 54k abstracts
from
medical journals in his information retrieval class (no
fair using this if you've taken the IR class already; play with
a different data set). Or be creative: use your own email
corpus. Or phone text message corpus. Just be sure
that whatever data set you choose is large enough that you have
something interesting to experiment with.
Be sure to choose a large enough number of topics that your results will give you well delineated topics. Find a few interpretable topics and present them by showing the highest probability words (10-20) within the topic, and give a label to the topic. You may decide that P(W|T) isn't the best measure for interpreting a topic, since high frequency words will have high probability in every topic. Instead, you may prefer a discriminative measure such as P(W|T)P(T|W). (I just made up this measure. It's a total hack, but it combines how well a word predicts a topic and how well a topic predicts a word.)
Note: Depending on the number of word types in your collection, you may want to use a β < .01 to obtain sparser topics.
Be sure to choose a large enough number of topics that your results will give you well delineated topics. Find a few interpretable topics and present them by showing the highest probability words (10-20) within the topic, and give a label to the topic. You may decide that P(W|T) isn't the best measure for interpreting a topic, since high frequency words will have high probability in every topic. Instead, you may prefer a discriminative measure such as P(W|T)P(T|W). (I just made up this measure. It's a total hack, but it combines how well a word predicts a topic and how well a topic predicts a word.)
Note: Depending on the number of word types in your collection, you may want to use a β < .01 to obtain sparser topics.