Probabilistic
Models of
Human and Machine Intelligence
CSCI
7222
Assignment 6
Assigned
10/22/2013
Due 11/5/2013
Goal
The
goal of this assignment is to explore the topic model -- to see how it
can be implemented, applied to data, and how its hyperparameters affect
the outcome of the computation.
PART I
Download
and install a topic model simulator. A few that I've
been able to find are listed below, and I'm sure there are more out
there. For extra credit,
write
your own. The amount of code needed is pretty minimal to do
Gibbs
sampling, and all the equations are specified in my class notes or in
the text. Some of the packages will have default values for
parameters
(α, β)
and sampling procedure (# burn in iterations, # data collection
iterations). Make sure you pick a package that gives you enough
flexibility for the rest of the assignment; that is, you will need to
estimate P(T|D) and P(W|T) from the topic assignments.
UCI
Topic
modeling toolbox
Mallet (machine learning for language, Java based implementation of topic modeling)
Mahout (Java API that does topic modeling)
C implementation of topic models
windows executable of C implementation (runs from the command line)
Stanford Topic Modeling Toolkit Python implementation and documentation
R (statistics language) implementation and documentation
Mallet (machine learning for language, Java based implementation of topic modeling)
Mahout (Java API that does topic modeling)
C implementation of topic models
windows executable of C implementation (runs from the command line)
Stanford Topic Modeling Toolkit Python implementation and documentation
R (statistics language) implementation and documentation
PART II
Write
code for and run a generative topic model that produces synthetic
data. For this small scale example, generate 200
documents
each with 50 word tokens from a dictionary of 20 word types
and 3 topics. Use α=.1, β=.01.
Show a sample document.
Show a sample topic distribution---the a probability
table
over
the 20 word types representing P(Word|Topic) for some topic. To use
consistent notation across the class, label
your words A-T (the first 20 letters of the alphabet), so that a
document will be a string of 50 letters drawn from {A, ..., T}.
Hint: Barber's BRML Toolkit includes a function for drawing from a Dirichlet: dirrnd. There's other code on the web as well.
Hint: Barber's BRML Toolkit includes a function for drawing from a Dirichlet: dirrnd. There's other code on the web as well.
PART III
Run
your topic model with T=3, α=.1, β=.01
on your synthetic data set.
Compare the true topics (in your generative model) to the
recovered topics. The 'recovered topics' are the estimate of
P(Word | Topic) that comes from sampling. The 'true topics'
are
the P(Word | Topic) distributions like the one you showed in part II.
PART IV
The
bias α=.1 encourages sparse topic distributions and the
bias β=.01 encourages sparse distributions over words.
Change
one of these biases and find out how robust the results are to having
chosen parameters that match the underlying generative process.
You may wish to quanitfy how changing these parameters
affects
the results in terms of an entropy measure. For example, if
you
modify α, then you might want to compare the mean entropy of
topic distributions:
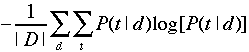
This is a measure of how focused the distribution of topics is on
average across documents. As you increase α, this entropy
should
increase. If you modify β, you can evaluate
the
consequence via the mean entropy of the word distribution:
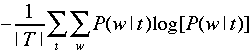
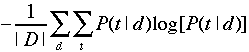
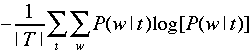
PART V
Run
the topic model, with parameters you select, on larger, interesting
data set. Data sets are abundant on the web. I only ask that
it
be an
English language data set so that other members of the class can see
and understand your results. The UCI Matlab Topic Modeling Toolbox
includes a variety of data
sets. There's also a
corpus of 2246 articles from the Associated
Press available from Blei at
Princeton. Jim Martin has a corpus of
54k abstracts
from medical journals in his
information retrieval class (no fair
using this if you've taken the IR class already; play with a different
data set). Or be creative: use
your own email corpus. Or phone text message corpus.
Just
be sure that whatever data set you choose is large enough that you have
something interesting to experiment with.
The Institute of Cognitive Science just purchased a subscript to a site called Sketch Engine that provides access to more than 80 corpora in dozens of languages. You can access the site via a hard-wired university computer, connected via WiFi to UCB Wireless (not as UCB Guest), or on the CU Boulder VPN. From the landing page, click on the "IP auth" link in the upper right corner of the page. It may be fun to apply topic models to corpora in your native language, but please translate and interpret your results for the sake of the lousy American professor who can barely speak one language.
Be sure to choose a large enough number of topics that your results will give you well delineated topics. Find a few interpretable topics and present them by showing the highest probability words (10-20) within the topic, and give a label to the topic. You may decide that P(W|T) isn't the best measure for interpreting a topic, since high frequency words will have high probability in every topic. Instead, you may prefer a discriminative measure such as P(W|T)P(T|W). (I just made up this measure. It's a total hack, but it combines how well a word predicts a topic and how well a topic predicts a word.)
Note: Depending on the number of word types in your collection, you may want to use a β < .01 to obtain sparser topics.
The Institute of Cognitive Science just purchased a subscript to a site called Sketch Engine that provides access to more than 80 corpora in dozens of languages. You can access the site via a hard-wired university computer, connected via WiFi to UCB Wireless (not as UCB Guest), or on the CU Boulder VPN. From the landing page, click on the "IP auth" link in the upper right corner of the page. It may be fun to apply topic models to corpora in your native language, but please translate and interpret your results for the sake of the lousy American professor who can barely speak one language.
Be sure to choose a large enough number of topics that your results will give you well delineated topics. Find a few interpretable topics and present them by showing the highest probability words (10-20) within the topic, and give a label to the topic. You may decide that P(W|T) isn't the best measure for interpreting a topic, since high frequency words will have high probability in every topic. Instead, you may prefer a discriminative measure such as P(W|T)P(T|W). (I just made up this measure. It's a total hack, but it combines how well a word predicts a topic and how well a topic predicts a word.)
Note: Depending on the number of word types in your collection, you may want to use a β < .01 to obtain sparser topics.