The goal of this assignment is to give you more experience manipulating probabilities, performing Bayesian inference, and exploring the Weiss et al. (2002) motion perception model. You will also get some practice with Gaussian distributions.

In the 9/19 lecture, I provided MATLAB code (slide 7) that implements Bayesian updating of a discrete hypothesis space for the bias of a coin (slide 6). I want you to modify my code to implement the continuous hypothesis space (slide 9) using the Beta density.  In matlab, betapdf is the Beta probability density function and betacdf is the cumulative distribution function. Note that when you make plots, you will necessarily sample the continuous density at discrete points. Hand in your code as well as your figure.

I have written MATLAB code, weissSimulation.m, which generates 3 different image examples each consisting of two image snapshots at successive points in time.  The images are shown below, with red pixels being on in snapshot 1, green on in snapshot 2, and yellow on in both snapshots 1 and 2.

My code also computes the (unscaled) log likelihood of motion in each possible direction.  The velocities are specified by horizontal and vertical components in {-2, -1, 0, 1, 2}.  For these three examples, the log likelihoods for  the possible velocities are depicted below.


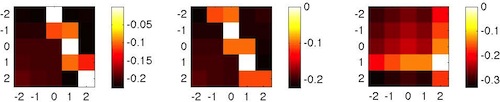
Remember that log likelihoods are nonpositive, and the largest possible log likelihood value is 0.  My code uses the expression for likelihood given on slide 24 of the lecture notes on the upper half of the slide (which computes a squared difference between corresponding pixels in the two snapshots).

With the log likelihoods, you can select the ML (maximum likelihood) velocity.  For example, in the first example, the velocity vectors (1,0), (2,2) and (0,-2) are all equally likely interpretations of the motion; for the third example, the maximum likelihood velocity vector is (2,1).  For Part I of the homework, I want you to modify my code to compute the posterior distribution over likelihoods by incorporating Weiss's small-motion-bias prior with the free parameter σ²/σ_p². (Remember, the free parameter is a ratio of variances; there's only one parameter value to pick.)

Hand in this posterior distribution over velocities for two values of the constant, and indicate the two values you've chosen.  Try to choose constants such that the MAP solution is different for the two values.  The posterior distribution over velocities should look like the likelihood ditsribution (and you can use the same matlab code), but it should incorporate the prior.

For part III of this assignment, you'll implement a model from scratch has a vague relationship to the Weiss et al. (2002) ambiguous-motion model.  The model will try to infer the direction of motion from some observations.  I'll assume that a rigid motion is being observed involving an object that has two distictinctive visual features.  The figure below shows a snapshot of the object at two nearby points in time.  The distinctive features are the red triangle and blue square.  Let's call them R and B for short.


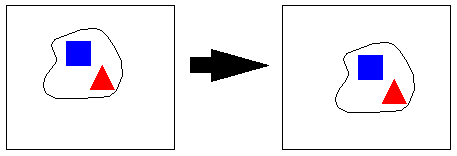
Because the features are distinctive, determining the correspondence between features at two snapshots in time is straightforward, and the velocity vector can be estimated.  Assume that these measurements are noisy however, such that the x and y components of the velocity are each corrupted by independent, mean zero Gaussian noise with standard deviation σ.   Thus the observation consists of four real valued numbers: Rx, Ry, Bx, and By -- respectively, the red element x and y velocities, and the blue element x and y velocities.  The goal of the model is to infer the direction of motion.

To simplify, let's assume there are only four directions: up, down, left, and right.  Further, the motions will all be one unit step.  Thus, if the motion is to the right, then noise-free observations would be:  Rx=1, Ry=0, Bx=1, By=0.  If the motion is down, then the noise-free observations would be: Rx=0, Ry=-1, Bx=0, By=-1.

Formally, the model must compute P(Direction | Rx, Ry, Bx, By).

Task 1

Task 2

Task 3

Task 4

I would like hardcopies of your work.   It's easier for you than putting together a single word / pdf document.  And it's easier for me than keeping tabs on electronic documents.  It would be good for you to hand in the code in case there's a problem with your results.