The Assignment:
Purpose: To use the BGI graphics library and to increase your skill in program design, use of nested loops, and use of functions.
The Exercise
Mandelbrot's fractal is a complex, colorful pattern that can be generated by a simple rule called the "escape-time algorithm":
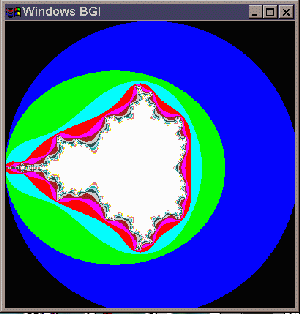
You will write a program that generates this pattern in a 401x401 graphics window. Here's a brief description of how the pattern is generated, followed by some discussion of programming issues:
How the Pattern is Generated:
Imagine the square graphics window as a part of the Cartesian plane, with the coordinate (0,0) in the center. The x-coordinates range from -2 on the left to +2 on the right. The y-coordinates range from -2 on the top to +2 on the bottom (which is backwards from the usual y-coordinates, but the backwardness will make some of the programming easier). Within this square, you can pick any point, for example:
x = 0.5
y = 1.0
We will call this location our "starting point" (but keep in mind that
we could have started anywhere within the square). We can copy this
starting point to two new variables (moving_x and moving_y) which
will then move around the square in a series of jumps. Each jump
will move the "moving point" according to these equations:
- new value of moving_x = (old moving_x)² - (old moving_y)² + start_x;
- new value of moving y = 2 * (old moving_x) * (old moving_y) + start_y;
These steps can be repeated over and over again, to produce a series of points. For example:
- Starting point:
x = 0.5 and y = 1.0 - Initialize:
moving_x = 0.5 moving_y = 1.0 - After one jump:
moving_x = (old moving_x)² - (old moving_y)² + start_x = -0.25 moving_y = 2 * (old moving_x) * (old moving_y) + start_y = 2.00 - After two jumps:
moving_x = (old moving_x)² - (old moving_y)² + start_x = -3.44 moving_y = 2 * (old moving_x) * (old moving_y) + start_y = 0
For each point in the square, we can calculate the series of moving points that begins at the given point. Once a point jumps to a distance of 2.0 or further from the center, then we say that the point has "escaped". The "escape time" is the number of jumps that are required for a point. If a point has not escaped after 15 jumps, then we'll use the number 15 for the escape time--so that every point has an escape time in the range of 0 to 15.
Finally, here's how to generate the pattern: For each point in the square, calculate the escape time (from 0 to 15). Use this number as the color of the point in the BGI putpixel command.
Useful Const Declarations for Your Program
My implementation of the program includes these useful global constants at the top:
const int LIMIT = 15; // Maximum jumps allowed const int PIXEL_SIZE = 401; // Width & height of screen in pixels const double CARTESIAN_MAX = 2.0; // Maximum Cartesian coordinate value
Overall Design of the Program
The main program should open the graphics window, then draw the fractal pattern. In order to draw the pattern, you'll need nested for-loops: an outer loop that steps through each possible x value for a pixel, and an inner loop that steps through each possible y value for a pixel. Within the loops, you should calculate the escape time for the point, and use that escape time as the color in a call to the putpixel function.
Notice that the two for-loops are controlled by variables x and y which range through the possible pixel values. But these x and y values are not in the Cartesian coordinate system. Because of this, it might make sense to use a different name for the pixel values: perhaps pixel_x and pixel_y. Before you calculate the escape time, you must convert pixel_x (ranging from 0 to PIXEL_SIZE-1) to an ordinary Cartesian coordinate (ranging from -2.0 to 2.0) and also convert the pixel_y to an ordinary Cartesian coordinate. To do these conversions, you must write a function with this prototype:
// Function to convert a pixel coordinate // (in the range from 0 to PIXEL_MAX-1) // to its corresponding Cartesian value // (in the range from // -1*CARTESIAN_MAX to CARTESIAN_MAX). double pixel_to_cart(int pixel);The TA will require you to have a correct function with this exact prototype as part of your submission.
The rest of your program design is up to you, although your TA will have one more requirement that you implement and use two functions with these prototypes:
double distance_from_origin(double x, double y); int escape_color(double x, double y);The distance_from_origin function computes the distance between (x,y) and the center (0,0) in the Cartesian coordinate system. Your implementation will probably call the sqrt function (and you must include
Style
You are required to follow the style guide from www.cs.colorado.edu/~main/style.html. Part of your grade will be based on how well you follow the guide. Also, if you fail to follow these rules, then none of the instructors will provide any help.
Code Review
Part of your grade will be given when you review your code with a TA and at least one other student during your recitation on Feb 28. If you miss this recitation without a medical excuse, then you can't receive the points for the code review. During the code review, you will show your code to another person, explain how it works, and check that it meets all requirements of the style guide.
Points
- Preliminary points: 5
- Submission of correctly compiled program before recitation: 10
- Correctness: 20
- Code review during recitation on Feb 28: 5
Grading
Grading of your final corrected version will follow this rubric.
Extra Work
There's no extra credit available, but you might enjoy some extensions (I know a lot of you have spare time on your hands). One extension is to expand the LIMIT beyond 15 different interesting colors for each of the different escape times. You should read about the COLOR function in the bgi documentation to determine how to create interesting colors.
Another fun extension is to incorporate some mechanism to recenter and zoom in on the fractal.
We'll talk about these extensions in March.
![[CAUTION!]](http://www.cs.colorado.edu/~main/images/caution.gif)