A connected set cannot be written as the union of two closed, disjoint subsets.
A simply connected set can be contracted to a point.
The connected component of a point is the largest connected subset containing that point.
A closed set is disconnected if it can be split into two parts, A and B, such that min |a-b| > 0 for a in A and b in B. (That is, it has a gap in it.)
A totally disconnected set is one in which the connected component of each point is itself, and itself alone.
A closed set is one that includes its boundary (or, equivalently, all of its limit points).
A perfect set, common in the study of dynamical systems, has no isolated points (or, equivalently, every point in a perfect set is a limit point).
An epsilon chain is a finite sequence of points x_0 ... x_N that are separated by distances of epsilon or less: |x_i - x_i+1| < eps.
Two points are epsilon connected if there is an epsilon chain joining them.
Any two points in an epsilon-connected set can be linked by an epsilon chain.
A epsilon-isolated point is an epsilon-component consisting of a single point.
A epsilon-connected component is a maximal epsilon-connected subset.
A fractal, loosely speaking, is an object that is self similar: it contains "copies" of itself. Zooming in on a fractal always reveals more detail in the structure. Fractals have noninteger Hausdorff dimension. The prototypical example is the Cantor set, which is constructed by removing some portion of a line segment (say, the middle third) ad infinitum.
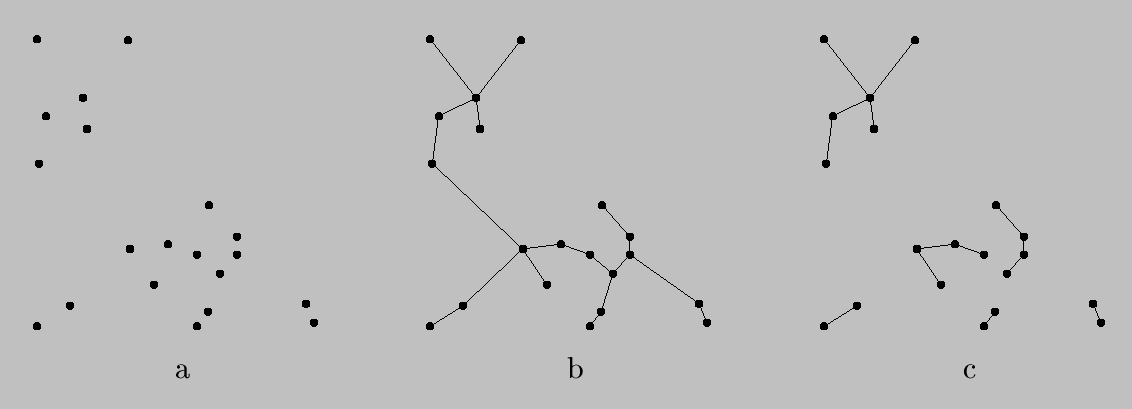
A tree is a graph with no cycles (loops).
The minimal spanning tree is the tree of minimum total branch length that spans the data. To construct the MST, one starts with any point and its nearest neighbor, adds the closest point, and repeats until all points are in the tree (Prim's algorithm). See the center image below for an example.
 |
An iterated function system is a (fairly general) method for generating a fractal as the attracting fixed set of a multi-image map. For example, the Sierpinski triangle, T is the set invariant under the union of 3 linear transformations: T = f1[T] u f2[T] u f3[T] with
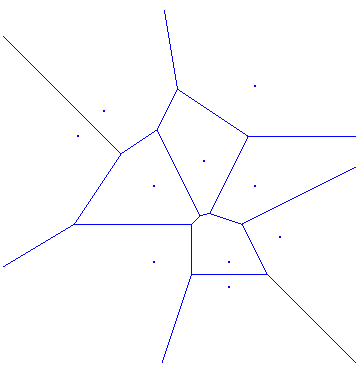
The Voronoi diagram of a set of points p_1,...,p_N is a division of space into regions V(p_i) such that every point x in V(p_i) is closer to p_i than to any other data point. See below for an example.
 |
The Delaunay triangulation is the geometric dual obtained from the Voronoi diagram by drawing an edge between two data points if their Voronoi cells share a face, a triangle when three cells intersect, and so on. See below for an example.
 |
The alpha shape algorithm "fattens" a set by a radius alpha. It introduces a resolution parameter, alpha, to generate subsets of the Voronoi diagram and Delaunay triangulation. This allows it to capture different levels of detail about an object. Click here or here to see some related webpages.