Though it is not necessarily the view taken by those who design them, modern computers are deterministic nonlinear dynamical systems, and it is both interesting and useful to treat them as such. We have showed that the dynamics of a computer can be described by an iterated map with two components, one dictated by the hardware and one dictated by the software. Using a custom measurement infrastructure to get at the internal variables of these million-transistor systems without disturbing their dynamics, we gathered time-series data from a variety of simple programs running on two common microprocessors, then used delay-coordinate embedding to study the associated dynamics. We found strong indications, from multiple corroborating methods, of a low-dimensional attractor in the dynamics of a simple, three-instruction loop running on an Intel Core2-based machine, including the first experimental evidence of chaos in real computer hardware. When we ran the same program on an Intel Pentium 4-based machine, the dynamics became periodic; when we reordered the instructions in the program, extra loops appeared in the attractor, increasing its dimension from 0.8 to 1.1 and decreasing its largest Lyapunov exponent by 25%. When we alternated between the two programs, the reconstructed trajectory alternated between the corresponding attractors, leading us to a view of a computer as a dynamical system operating under the influence of a series of bifurcations induced by the code that it is running.
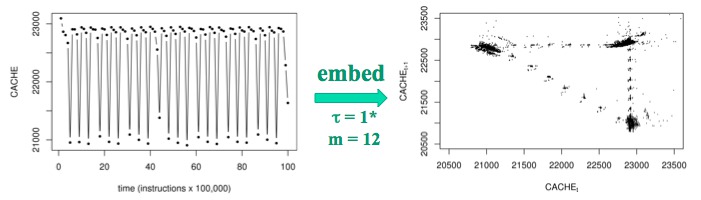
Cache-miss dynamics of a simple, three-instruction loop running on
a Core 2-based machine are chaotic:

Cache-miss dynamics of the same code running on a Pentium-4 based
machine are periodic:
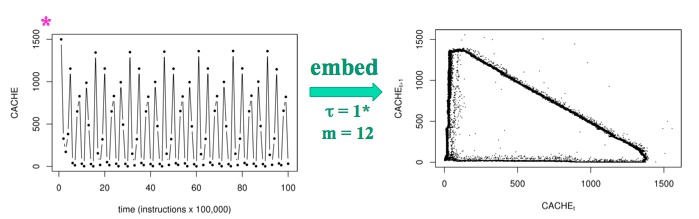
Somewhat surprisingly, the topological dimension of the embedding space was similar (m=10 to 15) in all of these experiments, which is probably a reflection of the constraints imposed on these systems by the x86 design specification that both machines follow. All of these low dimensions - attractors with dimension of approximately 1 in state spaces with a smallish number of axes - are somewhat surprising in a system as complex as a microprocessor. Computers are organized by design into a small number of tightly coupled subsystems, however, which greatly reduces the effective number of degrees of freedom in the system.
These results, which are addressed at more length in the 2009 CHAOS paper cited below, are not only interesting from a dynamics standpoint; they are also important for the purposes of computer simulation and design. These engineered systems have grown so complicated as to defy the analysis tools that are typically used by their designers: tools that assume linearity and stochasticity, and essentially ignore dynamics. The ideas and methods developed by the nonlinear dynamics community, applied and interpreted in the context of the framework proposed here, are a much better way to study, understand, and design modern computer systems.
If computers are deterministic systems, then one should be able to use deterministic forecast rules to predict their behavior. We have explored a couple of deterministic modeling schemes, which are described at more length in the 2011 IDA paper cited below. It turns out that these models produce accurate forecasts in some cases, but not all. The memory and processor loads of some simple programs are easy to predict, for example, but those of more-complex programs like gcc are not. Accurate forecasts of these quantities, if one could construct them, could be used to improve computer design. If one could predict that a particular computational thread would be bogged down for the next 0.6 seconds waiting for data from main memory, for instance, one could save power by putting that thread on hold for that time period (e.g., by migrating it to a processing unit whose clock speed is scaled back).
We conjecture that, in practice, complexity can effectively overwhelm the predictive power of deterministic forecast models. To explore that, we build models of a number of performance traces from different programs running on different Intel-based computers. We then calculate the permutation entropy - a temporal entropy metric that uses ordinal analysis - of those traces and correlate those values against the prediction success. A paper on these results is currently in review.
One of the challenges in analyzing or modeling computer performance data using dynamical-systems techniques is the nonstationary nature of the data. We approach this notoriously challenging problem using computational topology: leveraging fundamental properties like continuity and connectedness to pull apart different regimes in these complicated signals:
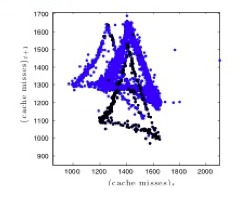
These algorithms, and their results, are described at more length in the 2012 CHAOS paper cited below.
