There are two types of driver routines for the SVD. In both,
the computation proceeds in the following stages:
- 1.
- The matrix A is reduced to bidiagonal
form: A=U1 B V1T if
A is real (A=U1 B V1H if A is complex), where U1 and V1
are orthogonal (unitary if A is complex), and B is real and
upper-bidiagonal when
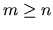 and lower bidiagonal when m < n, so
that B is nonzero only on the main diagonal and either on the first
superdiagonal (if
and lower bidiagonal when m < n, so
that B is nonzero only on the main diagonal and either on the first
superdiagonal (if 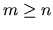 )
or the first subdiagonal (if m<n).
)
or the first subdiagonal (if m<n).
- 2.
- The SVD of the bidiagonal matrix B is computed:
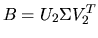 ,
where U2 and V2 are orthogonal and
,
where U2 and V2 are orthogonal and 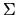 is diagonal as described
above. The singular vectors of A are then U = U1 U2 and
V = V1 V2.
is diagonal as described
above. The singular vectors of A are then U = U1 U2 and
V = V1 V2.
The drivers differ in how the SVD of the bidiagonal matrix is computed.
- a simple driver
xGESVD
computes all the singular values and (optionally) left and/or right
singular vectors via the Golub-Reinsch QR algorithm [55].
- a divide and conquer driver
xGESDD solves the same problem
as the simple driver. It is much faster than the simple driver
for large matrices, but uses more workspace. The name divide-and-conquer
refers to the underlying algorithm
(see sections 2.4.4 and 3.4.3).
Table 2.5:
Driver routines for singular value problems
| Type of |
Function and storage scheme |
Single precision |
Double precision |
| problem |
|
real |
complex |
real |
complex |
| SVD |
simple driver |
SGESVD |
CGESVD |
DGESVD |
ZGESVD |
| |
divide and conquer driver |
SGESDD |
CGESDD |
DGESDD |
ZGESDD |
1999-12-26